1 . 已知椭圆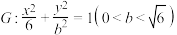 的左、右焦点分别为
的左、右焦点分别为 、
、 ,短轴的两个端点分别为
,短轴的两个端点分别为 、
、 ,点
,点 在椭圆
在椭圆 上,且满足
上,且满足 .当
.当 变化时,给出下列四个命题:①点
变化时,给出下列四个命题:①点 的轨迹关于
的轨迹关于 轴对称;②存在
轴对称;②存在 使得椭圆
使得椭圆 上满足条件的点
上满足条件的点 仅有两个;③
仅有两个;③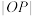 的最小值为2;④
的最小值为2;④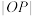 最大值为
最大值为 ,其中正确命题的序号是
,其中正确命题的序号是___________ .
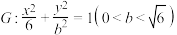 的左、右焦点分别为
的左、右焦点分别为 、
、 ,短轴的两个端点分别为
,短轴的两个端点分别为 、
、 ,点
,点 在椭圆
在椭圆 上,且满足
上,且满足 .当
.当 变化时,给出下列四个命题:①点
变化时,给出下列四个命题:①点 的轨迹关于
的轨迹关于 轴对称;②存在
轴对称;②存在 使得椭圆
使得椭圆 上满足条件的点
上满足条件的点 仅有两个;③
仅有两个;③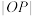 的最小值为2;④
的最小值为2;④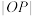 最大值为
最大值为 ,其中正确命题的序号是
,其中正确命题的序号是
您最近一年使用:0次
2 . 已知某椭圆的焦点是 ,
, ,过点
,过点 并垂直于x轴的直线与椭圆的一个交点为B,且
并垂直于x轴的直线与椭圆的一个交点为B,且 ,椭圆上不同的两点A、C满足条件:
,椭圆上不同的两点A、C满足条件: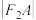 ,
, ,
,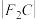 成等差数列,则弦AC中点的横坐标是
成等差数列,则弦AC中点的横坐标是________ ,设弦AC的垂直平分线的方程为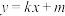 ,求m的取值范围是
,求m的取值范围是________ .
 ,
, ,过点
,过点 并垂直于x轴的直线与椭圆的一个交点为B,且
并垂直于x轴的直线与椭圆的一个交点为B,且 ,椭圆上不同的两点A、C满足条件:
,椭圆上不同的两点A、C满足条件: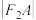 ,
, ,
,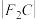 成等差数列,则弦AC中点的横坐标是
成等差数列,则弦AC中点的横坐标是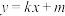 ,求m的取值范围是
,求m的取值范围是
您最近一年使用:0次
3 . 已知抛物线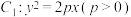 的焦点为
的焦点为 ,满足若过点
,满足若过点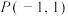 的直线交
的直线交 于
于 ,则有
,则有 .在
.在 上有三点构成等边三角形,其中心的轨迹记为
上有三点构成等边三角形,其中心的轨迹记为 ,则
,则 的轨迹方程为
的轨迹方程为___________ ,试给出一圆 ,使得对
,使得对 上任意一点
上任意一点 ,过点
,过点 作
作 的两条切线分别交
的两条切线分别交 于不同于
于不同于 的点
的点 ,则
,则 必为
必为 的切线:
的切线:___________ .
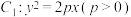 的焦点为
的焦点为 ,满足若过点
,满足若过点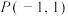 的直线交
的直线交 于
于 ,则有
,则有 .在
.在 上有三点构成等边三角形,其中心的轨迹记为
上有三点构成等边三角形,其中心的轨迹记为 ,则
,则 的轨迹方程为
的轨迹方程为 ,使得对
,使得对 上任意一点
上任意一点 ,过点
,过点 作
作 的两条切线分别交
的两条切线分别交 于不同于
于不同于 的点
的点 ,则
,则 必为
必为 的切线:
的切线:
您最近一年使用:0次
名校
解题方法
4 . 已知抛物线 的焦点为
的焦点为 ,直线
,直线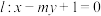 交抛物线于
交抛物线于 两点,
两点, 为抛物线
为抛物线 的准线与
的准线与 轴的交点,直线
轴的交点,直线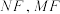 分别交抛物线于
分别交抛物线于 两点(点
两点(点 异于点
异于点 ,
, ),
), 为坐标原点,则实数
为坐标原点,则实数 的取值范围为
的取值范围为__________ ;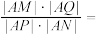
__________ .
 的焦点为
的焦点为 ,直线
,直线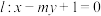 交抛物线于
交抛物线于 两点,
两点, 为抛物线
为抛物线 的准线与
的准线与 轴的交点,直线
轴的交点,直线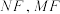 分别交抛物线于
分别交抛物线于 两点(点
两点(点 异于点
异于点 ,
, ),
), 为坐标原点,则实数
为坐标原点,则实数 的取值范围为
的取值范围为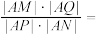
您最近一年使用:0次
2024-06-14更新
|
323次组卷
|
2卷引用:2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题
解题方法
5 . 已知椭圆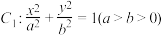 ,其长轴长为4且离心率为
,其长轴长为4且离心率为 ,在椭圆
,在椭圆 上任取一点
上任取一点 ,过点
,过点 作圆
作圆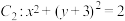 的两条切线
的两条切线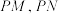 .切点分别为
.切点分别为 ,则
,则 的最小值为
的最小值为______ .
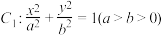 ,其长轴长为4且离心率为
,其长轴长为4且离心率为 ,在椭圆
,在椭圆 上任取一点
上任取一点 ,过点
,过点 作圆
作圆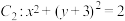 的两条切线
的两条切线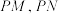 .切点分别为
.切点分别为 ,则
,则 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
6 . 在某城市中,F地位于E地的正南方向,相距2km;Q地位于E地的正东方向,相距1km.现有一条沿湖小径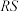 (曲线),其上任意一点到E和F的距离之和为4km.现计划在该小径上选择一个合适的点P建造一个观景台,经测算从P到F,Q两地修建观景步道的费用都是5万元/km,则修建两条观景步道的总费用最低是
(曲线),其上任意一点到E和F的距离之和为4km.现计划在该小径上选择一个合适的点P建造一个观景台,经测算从P到F,Q两地修建观景步道的费用都是5万元/km,则修建两条观景步道的总费用最低是___________ 万元.
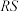 (曲线),其上任意一点到E和F的距离之和为4km.现计划在该小径上选择一个合适的点P建造一个观景台,经测算从P到F,Q两地修建观景步道的费用都是5万元/km,则修建两条观景步道的总费用最低是
(曲线),其上任意一点到E和F的距离之和为4km.现计划在该小径上选择一个合适的点P建造一个观景台,经测算从P到F,Q两地修建观景步道的费用都是5万元/km,则修建两条观景步道的总费用最低是
您最近一年使用:0次
解题方法
7 . 已知抛物线 ,从抛物线内一点
,从抛物线内一点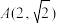 发出平行于
发出平行于 轴的光线经过扡物线上点
轴的光线经过扡物线上点 反射后交抛物线于点
反射后交抛物线于点 ,则
,则 的面积为
的面积为______ .
 ,从抛物线内一点
,从抛物线内一点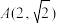 发出平行于
发出平行于 轴的光线经过扡物线上点
轴的光线经过扡物线上点 反射后交抛物线于点
反射后交抛物线于点 ,则
,则 的面积为
的面积为
您最近一年使用:0次
名校
8 . 长方体 中,
中,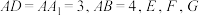 分别是棱
分别是棱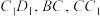 的中点,
的中点, 是该长方体的面
是该长方体的面 内的一个动点(不包括边界),若直线
内的一个动点(不包括边界),若直线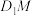 与平面
与平面 平行,则
平行,则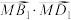 的最小值为
的最小值为______ .
 中,
中,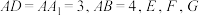 分别是棱
分别是棱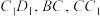 的中点,
的中点, 是该长方体的面
是该长方体的面 内的一个动点(不包括边界),若直线
内的一个动点(不包括边界),若直线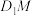 与平面
与平面 平行,则
平行,则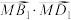 的最小值为
的最小值为
您最近一年使用:0次
9 . 对于空间向量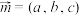 ,定义
,定义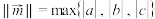 ,其中
,其中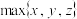 表示
表示 ,
, ,
, 这三个数的最大值.若
这三个数的最大值.若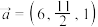 ,
,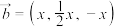 .①则
.①则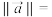
________ ;②当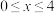 ,则
,则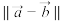 的最小值
的最小值________ .
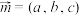 ,定义
,定义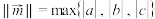 ,其中
,其中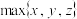 表示
表示 ,
, ,
, 这三个数的最大值.若
这三个数的最大值.若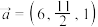 ,
,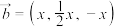 .①则
.①则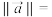
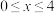 ,则
,则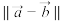 的最小值
的最小值
您最近一年使用:0次
2024-10-22更新
|
98次组卷
|
2卷引用:广东实验中学越秀学校2024-2025学年高二上学期10月月考数学试题
名校
10 . 双曲线的离心率可以与其渐近线有关,比如函数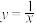 的图象是双曲线,它的实轴在直线
的图象是双曲线,它的实轴在直线 上,虚轴在直线
上,虚轴在直线 上,实轴顶点是
上,实轴顶点是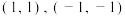 ,焦点坐标是
,焦点坐标是 ,
,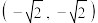 ,离心率为
,离心率为 ,已知函数
,已知函数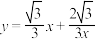 的图象也是双曲线,其离心率为
的图象也是双曲线,其离心率为 .则其在一象限内的焦点横坐标是
.则其在一象限内的焦点横坐标是__________ ,其离心率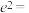
__________ .
 的图象是双曲线,它的实轴在直线
的图象是双曲线,它的实轴在直线 上,虚轴在直线
上,虚轴在直线 上,实轴顶点是
上,实轴顶点是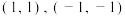 ,焦点坐标是
,焦点坐标是 ,
,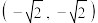 ,离心率为
,离心率为 ,已知函数
,已知函数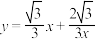 的图象也是双曲线,其离心率为
的图象也是双曲线,其离心率为 .则其在一象限内的焦点横坐标是
.则其在一象限内的焦点横坐标是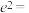
您最近一年使用:0次



