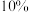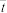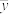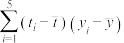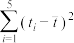解题方法
1 . 直播带货是扶贫助农的一种新模式,这种模式是利用主流媒体的公信力,聚合销售主播的力量助力打通农产品产销链条,切实助力农民增收.我国南方某蜜桔种植县通过网络平台直播销售蜜桔,其中每箱蜜桔重5千克,单价为40元/箱,已知最近5天单日直播总时长x(即所有主播的直播时长之和,单位:小时)与蜜桔的单目销售量y(单位:百箱)之间的统计数据如下表:
可用线性回归模型拟合y与x之间的关系.
(1)试求变量y与x的线性回归方程 ;
;
(2)若每位主播每天直播的时间不超过4小时,要使每天直播带货销售蜜桔的总金额超过60万元,则至少要请几位主播进行直播?
(3)直播带货大大提升销量的同时,也增加了坏果赔付的成本.该蜜桔平均每箱按80个计算,若客户在收到货时有坏果,则每个坏果要赔付1元.现有甲、乙两款包装箱,若采用甲款包装箱,成本为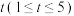 元/箱,且每箱坏果的个数X服从
元/箱,且每箱坏果的个数X服从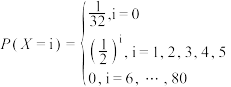 ;若采用乙款包装箱,成本为
;若采用乙款包装箱,成本为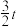 元/箱,且每箱坏果的个数Y服从
元/箱,且每箱坏果的个数Y服从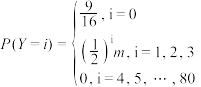 .请运用概率统计的相关知识分析,选择哪款包装箱获得的利润更大?
.请运用概率统计的相关知识分析,选择哪款包装箱获得的利润更大?
附: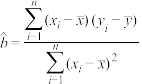 ,
, ,
,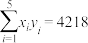 ,
,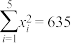 .
.
直播总时长x | 8 | 9 | 11 | 12 | 15 |
单日销售量y | 67 | 63 | 80 | 80 | 85 |
(1)试求变量y与x的线性回归方程
 ;
;(2)若每位主播每天直播的时间不超过4小时,要使每天直播带货销售蜜桔的总金额超过60万元,则至少要请几位主播进行直播?
(3)直播带货大大提升销量的同时,也增加了坏果赔付的成本.该蜜桔平均每箱按80个计算,若客户在收到货时有坏果,则每个坏果要赔付1元.现有甲、乙两款包装箱,若采用甲款包装箱,成本为
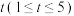 元/箱,且每箱坏果的个数X服从
元/箱,且每箱坏果的个数X服从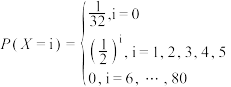 ;若采用乙款包装箱,成本为
;若采用乙款包装箱,成本为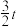 元/箱,且每箱坏果的个数Y服从
元/箱,且每箱坏果的个数Y服从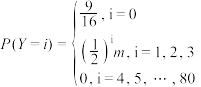 .请运用概率统计的相关知识分析,选择哪款包装箱获得的利润更大?
.请运用概率统计的相关知识分析,选择哪款包装箱获得的利润更大?附:
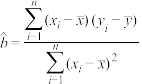 ,
, ,
,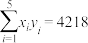 ,
,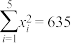 .
.
您最近一年使用:0次
2024·全国·模拟预测
2 . 向“新”而行,向“新”而进,新质生产力能够更好地推动高质量发展.以人工智能的应用为例,人工智能中的文生视频模型Sora(以下简称Sora),能够根据用户的文本提示创建最长60秒的逼真视频.为调查Sora的应用是否会对视频从业人员的数量产生影响,某学校研究小组随机抽取了120名视频从业人员进行调查,结果如下表所示.
(1)根据所给数据完成上表,依据小概率值 的独立性检验,能否认为Sora的应用与视频从业人员的减少有关?
的独立性检验,能否认为Sora的应用与视频从业人员的减少有关?
(2)某公司视频部现有员工100人,公司拟开展Sora培训,分三轮进行,每位员工第一轮至第三轮培训达到“优秀”的概率分别为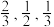 ,每轮相互独立,有二轮及以上获得“优秀”的员工才能应用Sora.
,每轮相互独立,有二轮及以上获得“优秀”的员工才能应用Sora.
(ⅰ)求员工经过培训能应用Sora的概率.
(ⅱ)已知开展Sora培训前,员工每人每年平均为公司创造利润6万元;开展Sora培训后,能应用Sora的员工每人每年平均为公司创造利润10万元;Sora培训平均每人每年成本为1万元.根据公司发展需要,计划先将视频部的部分员工随机调至其他部门,然后开展Sora培训,现要求培训后视频部的年利润不低于员工调整前的年利润,则视频部最多可以调多少人到其他部门?
附: ,其中
,其中 .
.
| Sora的应用情况 | 视频从业人员 | 合计 | |
| 减少 | 未减少 | ||
| 应用 | 70 | 75 | |
| 没有应用 | 15 | ||
| 合计 | 100 | 120 | |
(1)根据所给数据完成上表,依据小概率值
 的独立性检验,能否认为Sora的应用与视频从业人员的减少有关?
的独立性检验,能否认为Sora的应用与视频从业人员的减少有关?(2)某公司视频部现有员工100人,公司拟开展Sora培训,分三轮进行,每位员工第一轮至第三轮培训达到“优秀”的概率分别为
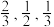 ,每轮相互独立,有二轮及以上获得“优秀”的员工才能应用Sora.
,每轮相互独立,有二轮及以上获得“优秀”的员工才能应用Sora.(ⅰ)求员工经过培训能应用Sora的概率.
(ⅱ)已知开展Sora培训前,员工每人每年平均为公司创造利润6万元;开展Sora培训后,能应用Sora的员工每人每年平均为公司创造利润10万元;Sora培训平均每人每年成本为1万元.根据公司发展需要,计划先将视频部的部分员工随机调至其他部门,然后开展Sora培训,现要求培训后视频部的年利润不低于员工调整前的年利润,则视频部最多可以调多少人到其他部门?
附:
 ,其中
,其中 .
. | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-19更新
|
1271次组卷
|
4卷引用:河南省郑州市部分学校2024届高三下学期高考临考预测数学试题
名校
解题方法
3 . 汽车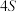 店是一种以“四位一体”为核心的特许经营模式,包括整车销售、零配件销售、售后服务、信息反馈等.某品牌汽车
店是一种以“四位一体”为核心的特许经营模式,包括整车销售、零配件销售、售后服务、信息反馈等.某品牌汽车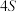 店为了了解
店为了了解 ,
, ,
, 三种类型汽车质量问题,对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1.
三种类型汽车质量问题,对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1.
表1
(1)某公司一次性从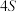 店购买该品牌
店购买该品牌 ,
, ,
, 型汽车各一辆,记
型汽车各一辆,记 表示这三辆车的一年内需要维修的车辆数,求
表示这三辆车的一年内需要维修的车辆数,求 的分布列及数学期望.(各型汽车维修的频率视为其需要维修的概率).
的分布列及数学期望.(各型汽车维修的频率视为其需要维修的概率).
(2)该品牌汽车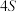 店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
预计在今后的销售中,销量与单价仍然服从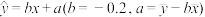 的关系,且该产品的成本是500元/件,为使
的关系,且该产品的成本是500元/件,为使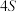 店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元?
店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元?
表1
表2
 店是一种以“四位一体”为核心的特许经营模式,包括整车销售、零配件销售、售后服务、信息反馈等.某品牌汽车
店是一种以“四位一体”为核心的特许经营模式,包括整车销售、零配件销售、售后服务、信息反馈等.某品牌汽车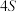 店为了了解
店为了了解 ,
, ,
, 三种类型汽车质量问题,对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1.
三种类型汽车质量问题,对售出的三种类型汽车各取100辆进行跟踪服务,发现各车型一年内需要维修的车辆如下表所示1.表1
(1)某公司一次性从
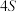 店购买该品牌
店购买该品牌 ,
, ,
, 型汽车各一辆,记
型汽车各一辆,记 表示这三辆车的一年内需要维修的车辆数,求
表示这三辆车的一年内需要维修的车辆数,求 的分布列及数学期望.(各型汽车维修的频率视为其需要维修的概率).
的分布列及数学期望.(各型汽车维修的频率视为其需要维修的概率).(2)该品牌汽车
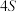 店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.
店为了对厂家新研发的一种产品进行合理定价,将该产品按使事先拟定的各种价格进行试销相等时间,得到数据如表2.预计在今后的销售中,销量与单价仍然服从
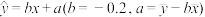 的关系,且该产品的成本是500元/件,为使
的关系,且该产品的成本是500元/件,为使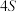 店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元?
店获得最大利润(利润=销售收入-成本),该产品的单价应定位多少元?表1
| 车型 |  |  |  |
| 频数 | 20 | 20 | 40 |
单价 (元) (元) | 800 | 820 | 840 | 860 | 880 | 900 |
销量 (件) (件) | 90 | 84 | 83 | 80 | 75 | 68 |
您最近一年使用:0次
4 . 某水果店的草莓每盒进价20元,售价30元,草莓保鲜度为两天,若两天之内未售出,以每盒10元的价格全部处理完.店长为了决策每两天的进货量,统计了本店过去40天草莓的日销售量(单位:十盒),获得如下数据:
假设草莓每日销量相互独立,且销售量的分布规律保持不变,将频率视为概率.
(1)记每两天中销售草莓的总盒数为X(单位:十盒),求X的分布列和数学期望;
(2)以两天内销售草莓获得利润较大为决策依据,在每两天进16十盒,17十盒两种方案中应选择哪种?
| 日销售量/十盒 | 7 | 8 | 9 | 10 |
| 天数 | 8 | 12 | 16 | 4 |
(1)记每两天中销售草莓的总盒数为X(单位:十盒),求X的分布列和数学期望;
(2)以两天内销售草莓获得利润较大为决策依据,在每两天进16十盒,17十盒两种方案中应选择哪种?
您最近一年使用:0次
名校
解题方法
5 . 近两年旅游业迎来强劲复苏,外出旅游的人越来越多. 两家旅游公司过去6个月的利润率统计如下:
两家旅游公司过去6个月的利润率统计如下:
利润率 ,盈利为正,亏损为负,且每个月的成本不变.
,盈利为正,亏损为负,且每个月的成本不变.
(1)比较 两家旅游公司过去6个月平均每月利润率的大小;
两家旅游公司过去6个月平均每月利润率的大小;
(2)用频率估计概率,且假设 两家旅游公司每个月的盈利情况是相互独立的,求未来的某个月
两家旅游公司每个月的盈利情况是相互独立的,求未来的某个月 两家旅游公司至少有一家盈利的概率.
两家旅游公司至少有一家盈利的概率.
 两家旅游公司过去6个月的利润率统计如下:
两家旅游公司过去6个月的利润率统计如下:利润率 月数 公司 |
|
| -5% |
A公司 | 3 | 2 | 1 |
B公司 | 2 | 2 | 2 |
 ,盈利为正,亏损为负,且每个月的成本不变.
,盈利为正,亏损为负,且每个月的成本不变.(1)比较
 两家旅游公司过去6个月平均每月利润率的大小;
两家旅游公司过去6个月平均每月利润率的大小;(2)用频率估计概率,且假设
 两家旅游公司每个月的盈利情况是相互独立的,求未来的某个月
两家旅游公司每个月的盈利情况是相互独立的,求未来的某个月 两家旅游公司至少有一家盈利的概率.
两家旅游公司至少有一家盈利的概率.
您最近一年使用:0次
名校
6 . 为贯彻中共中央、国务院2023年一号文件,某单位在当地定点帮扶某村种植一种草莓,并把这种露天种植的草莓搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的草莓的箱数 (单位:箱)与成本
(单位:箱)与成本 (单位:千元)的关系如下:
(单位:千元)的关系如下:
 与
与 可用回归方程
可用回归方程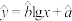 (其中
(其中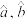 为常数)进行模拟.
为常数)进行模拟.

(1)若农户卖出的该草莓的价格为150元/箱,试预测该水果100箱的利润是多少元.(利润=售价-成本)
(2)据统计,1月份的连续16天中农户每天为甲地可配送的该水果的箱数的频率分布直方图如图,用这16天的情况来估计相应的概率.一个运输户拟购置 辆小货车专门运输农户为甲地配送的该水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元;若未发车,则每辆车每天平均亏损200元.试比较
辆小货车专门运输农户为甲地配送的该水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元;若未发车,则每辆车每天平均亏损200元.试比较 和
和 时,此项业务每天的利润平均值的大小.
时,此项业务每天的利润平均值的大小.
参考数据与公式:设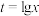 ,则
,则
线性回归直线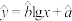 中,
中,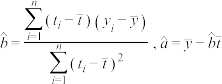 .
.
 (单位:箱)与成本
(单位:箱)与成本 (单位:千元)的关系如下:
(单位:千元)的关系如下:
| 1 | 3 | 4 | 6 | 7 |
| 5 | 6.5 | 7 | 7.5 | 8 |
 与
与 可用回归方程
可用回归方程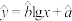 (其中
(其中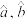 为常数)进行模拟.
为常数)进行模拟.
(1)若农户卖出的该草莓的价格为150元/箱,试预测该水果100箱的利润是多少元.(利润=售价-成本)
(2)据统计,1月份的连续16天中农户每天为甲地可配送的该水果的箱数的频率分布直方图如图,用这16天的情况来估计相应的概率.一个运输户拟购置
 辆小货车专门运输农户为甲地配送的该水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元;若未发车,则每辆车每天平均亏损200元.试比较
辆小货车专门运输农户为甲地配送的该水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元;若未发车,则每辆车每天平均亏损200元.试比较 和
和 时,此项业务每天的利润平均值的大小.
时,此项业务每天的利润平均值的大小.参考数据与公式:设
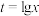 ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
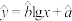 中,
中,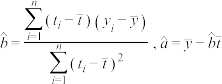 .
.
您最近一年使用:0次
2023-02-03更新
|
861次组卷
|
9卷引用:2020届河南省安阳市高三年级第一次模拟数学理科试题
2020届河南省安阳市高三年级第一次模拟数学理科试题(已下线)专题10 概率与统计-2020年高三数学(理)3-4月模拟试题汇编(已下线)易错点11 概率统计-备战2021年新高考数学一轮复习易错题(已下线)综合测试卷(巅峰版)突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)第二章随机变量及其分步单元测试(基础版) -突破满分数学之2019-2020学年高二数学(理)重难点突破(人教A版选修2-3)(已下线)第三章统计案例单元测试(基础版) -突破满分数学之2019-2020学年高二数学(理)课时训练(人教A版选修2-3)湖南省长沙市雅礼中学2023届高三下学期月考(六)数学试题(已下线)专题03 概率统计(理)第三篇-备战2020高考数学黄金30题系列之压轴题(新课标版)安徽省定远中学2023届高三下学期考前押题数学试卷
7 . 某企业对生产设备进行优化升级,升级后的设备控制系统由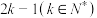 个相同的元件组成,每个元件正常工作的概率均为p(0<p<1),各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
个相同的元件组成,每个元件正常工作的概率均为p(0<p<1),各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为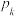 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).
(1)若 ,当k=2时,求控制系统中正常工作的元件个数X的分布列和数学期望,并求
,当k=2时,求控制系统中正常工作的元件个数X的分布列和数学期望,并求 ;
;
(2)已知设备升级前,单位时间的产量为a件,每件产品的利润为4元,设备升级后,在正常运行状态下,单位时间的产量是原来的2倍,且出现了高端产品,每件产品成为高端产品的概率为 ,每件高端产品的利润是8元.记设备升级后单位时间内的利润为Y(单位:元).
,每件高端产品的利润是8元.记设备升级后单位时间内的利润为Y(单位:元).
(i)请用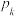 表示E(Y);
表示E(Y);
(ii)设备升级后,若将该设备的控制系统增加2个相同的元件,请分析是否能够提高E(Y).
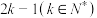 个相同的元件组成,每个元件正常工作的概率均为p(0<p<1),各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为
个相同的元件组成,每个元件正常工作的概率均为p(0<p<1),各元件之间相互独立.当控制系统有不少于k个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为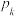 (例如:
(例如: 表示控制系统由3个元件组成时设备正常运行的概率;
表示控制系统由3个元件组成时设备正常运行的概率; 表示控制系统由5个元件组成时设备正常运行的概率).
表示控制系统由5个元件组成时设备正常运行的概率).(1)若
 ,当k=2时,求控制系统中正常工作的元件个数X的分布列和数学期望,并求
,当k=2时,求控制系统中正常工作的元件个数X的分布列和数学期望,并求 ;
;(2)已知设备升级前,单位时间的产量为a件,每件产品的利润为4元,设备升级后,在正常运行状态下,单位时间的产量是原来的2倍,且出现了高端产品,每件产品成为高端产品的概率为
 ,每件高端产品的利润是8元.记设备升级后单位时间内的利润为Y(单位:元).
,每件高端产品的利润是8元.记设备升级后单位时间内的利润为Y(单位:元).(i)请用
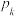 表示E(Y);
表示E(Y);(ii)设备升级后,若将该设备的控制系统增加2个相同的元件,请分析是否能够提高E(Y).
您最近一年使用:0次
2022-03-10更新
|
1150次组卷
|
4卷引用:河南省开封市2022届高三二模理科数学试题
河南省开封市2022届高三二模理科数学试题重庆市南开中学2022届高三下学期高考模拟数学试题(已下线)专题25 随机变量及其分布- 2022届高考数学一模试题分类汇编(新高考卷)广东省惠州市2024届高三上学期第二次调研数学试题
解题方法
8 . 某小区物业每天从供应商购进定量小包装果蔬,供本小区居民扫码自行购买,每份成本15元,售价20元.如果下午6点之前没有售完,物业将剩下的果蔬打五折于当天处理完毕.物业对20天本小区这种小包装果蔬下午6点之前的日需求量(单位:份)进行统计,得到如下条形图:
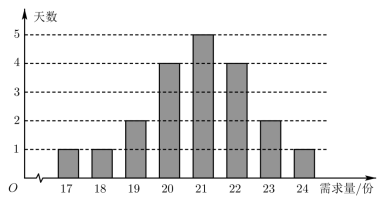
(1)假设物业某天购进20份果蔬,当天下午6点之前的需求量为n(单位:份,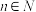 ).
).
(i)求日利润y(单位:元)关于n的函数解析式;
(ii)以20天记录的各需求量的频率作为各需求量发生的概率,求日利润不少于100元的概率.
(2)依据统计学知识,请设计一个方案,帮助物业决策每天购进的果蔬份数.只需说明原因,不需计算.

(1)假设物业某天购进20份果蔬,当天下午6点之前的需求量为n(单位:份,
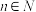 ).
).(i)求日利润y(单位:元)关于n的函数解析式;
(ii)以20天记录的各需求量的频率作为各需求量发生的概率,求日利润不少于100元的概率.
(2)依据统计学知识,请设计一个方案,帮助物业决策每天购进的果蔬份数.只需说明原因,不需计算.
您最近一年使用:0次
名校
9 . 2021年,我国脱贫攻坚战取得了全面胜利.为了巩固拓展脱贫攻坚成果,不断提高群众的幸福感,某县继续推进山羊养殖项目.为了建设相应的配套项目,该县主管部门对该县近年来山羊养殖业的规模进行了跟踪调查,得到了该县每年售卖山羊数量 (单位:万只)与相应年份代码
(单位:万只)与相应年份代码 的数据如下表:
的数据如下表:
(1)由表可知 与
与 有较强的线性相关关系,求
有较强的线性相关关系,求 关于
关于 的线性回归方程;
的线性回归方程;
(2)已知该县养殖的山羊品种只有甲、乙两种,且甲品种山羊与乙品种山羊的数量之比为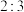 ,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:
,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:
以上述样本统计的养殖山羊所需时间情况估计全县养殖山羊所需时间(即以各养殖时间的频率作为各养殖时间的概率),且每月每只山羊的养殖成本为300元,结合(1)中所求回归方程,试求2022年该县养殖山羊所获利润的期望(假设山羊达到售卖标准后全部及时卖完).(利润=卖山羊的收入一山羊的养殖成本)
参考公式及数据:回归直线方程为 ,其中
,其中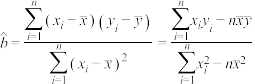 ,
,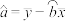 .
.
 (单位:万只)与相应年份代码
(单位:万只)与相应年份代码 的数据如下表:
的数据如下表:| 年份 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
售卖山羊数量 (万只) (万只) | 11 | 13 | 16 | 15 | 20 | 21 |
 与
与 有较强的线性相关关系,求
有较强的线性相关关系,求 关于
关于 的线性回归方程;
的线性回归方程;(2)已知该县养殖的山羊品种只有甲、乙两种,且甲品种山羊与乙品种山羊的数量之比为
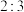 ,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:
,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:| 养殖时间(月数) | 6 | 7 | 8 | 9 |
| 甲品种山羊(只) | 20 | 35 | 35 | 10 |
| 乙品种山羊(只) | 10 | 30 | 40 | 20 |
参考公式及数据:回归直线方程为
 ,其中
,其中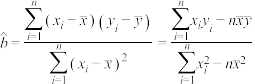 ,
,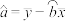 .
.
您最近一年使用:0次
2021-05-28更新
|
820次组卷
|
7卷引用:河南省焦作市2021届高三考前适应性考试数学(理科)数学试题
解题方法
10 . 某奶茶店推出一款新品奶茶,每杯成本为4元,售价为6元,如果当天卖不完,剩下的奶茶只能倒掉,奶茶店记录了60天这款新品奶茶的日需求量,整理得下表:
以这60天记录中各需求量的频率作为各需求量发生的概率.
(1)若奶茶店一天准备了35杯这款新品奶茶,用 表示当天销售这款新品奶茶的利润(单位:元),求
表示当天销售这款新品奶茶的利润(单位:元),求 的分布列和数学期望;
的分布列和数学期望;
(2)假设奶茶店每天准备的这款新品奶茶杯数都是5的倍数,有顾客建议店主每天准备40杯这款新品奶茶,你认为店主应该接受这个建议吗?请说明理由.
| 日需求量杯数 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 天数 | 5 | 5 | 10 | 15 | 10 | 10 | 5 |
(1)若奶茶店一天准备了35杯这款新品奶茶,用
 表示当天销售这款新品奶茶的利润(单位:元),求
表示当天销售这款新品奶茶的利润(单位:元),求 的分布列和数学期望;
的分布列和数学期望;(2)假设奶茶店每天准备的这款新品奶茶杯数都是5的倍数,有顾客建议店主每天准备40杯这款新品奶茶,你认为店主应该接受这个建议吗?请说明理由.
您最近一年使用:0次
2021-04-27更新
|
1100次组卷
|
3卷引用:河南省新乡市2021届高三第三次模拟考试数学(理科)试题
河南省新乡市2021届高三第三次模拟考试数学(理科)试题(已下线)押第19题 概率统计-备战2021年高考数学(理)临考题号押题(全国卷1)贵州省黔西南州金成实验学校2022-2023学年高二下学期5月月考数学试题