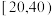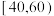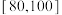1 . 为切实做好新冠疫情防控工作,有效、及时地控制和消除新冠肺炎的危害,增加学生对新冠肺炎预防知识的了解,某校举办了一次“新冠疫情”知识竞赛.竞赛分个人赛和团体赛两种.个人赛参赛方式为:组委会采取电脑出题的方式,从题库中随机出10道题,编号为 ,
, ,
, ,
, ,
, ,
,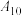 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
方案一:将班级选派的 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.
方案二:将班级选派的 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
 ,
, ,
, ,
, ,
, ,
,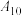 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:方案一:将班级选派的
 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.方案二:将班级选派的
 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为
 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数
 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
您最近一年使用:0次
名校
2 . 小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪 (单位:元)与送货单数
(单位:元)与送货单数 的函数关系式;
的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在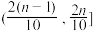
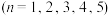 时,日平均派送量为
时,日平均派送量为 单.
单.
若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为 (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪 的分布列,数学期望及方差;
的分布列,数学期望及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据: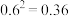 ,
, ,
, ,
,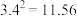 ,
,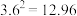 ,
,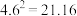 ,
,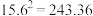 ,
, ,
,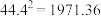 )
)
(1)请分别求出甲、乙两种薪酬方案中日薪
 (单位:元)与送货单数
(单位:元)与送货单数 的函数关系式;
的函数关系式;(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数满足以下条件:在这100天中的派送量指标满足如图所示的直方图,其中当某天的派送量指标在
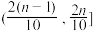
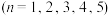 时,日平均派送量为
时,日平均派送量为 单.
单.若将频率视为概率,回答下列问题:

①根据以上数据,设每名派送员的日薪为
 (单位:元),试分别求出甲、乙两种方案的日薪
(单位:元),试分别求出甲、乙两种方案的日薪 的分布列,数学期望及方差;
的分布列,数学期望及方差;②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:
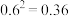 ,
, ,
, ,
,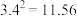 ,
,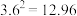 ,
,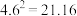 ,
,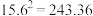 ,
, ,
,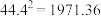 )
)
您最近一年使用:0次
2018-04-10更新
|
1071次组卷
|
3卷引用:河北省石家庄市2018届高三下学期一模考试数学(理)(A卷)试题
3 . 某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道题进行测试,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
您最近一年使用:0次
2024-04-02更新
|
2608次组卷
|
10卷引用:河北省承德市2023-2024学年高二年级下学期5月联考数学试题
河北省承德市2023-2024学年高二年级下学期5月联考数学试题广东省东莞市东华高级中学2022-2023学年高二下学期期中考试数学试卷(已下线)高二下学期期中模拟卷(新题型)(导数+计数原理+随机变量及其分布+统计)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)吉林省长春市第五中学2023-2024年高二下学期第二学程数学试题四川省眉山市彭山区第一中学2023-2024学年高二下学期5月月考数学试题(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)四川省仁寿第一中学校(北校区)2023-2024学年高二下学期7月期末考试数学试题青海省西宁市海湖中学2023-2024学年高二下学期第二阶段考试数学试卷江苏省扬州市仪征市精诚高级中学2023-2024学年高二下学期5月月考数学试题
名校
4 . 我市拟建立一个博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层师选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标问题中随机抽取3个问题,已知这6个招标问题中,甲公司能正确回答其中4道题目,而乙公司能正确回答每道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲公司至少答对2道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲公司至少答对2道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
您最近一年使用:0次
2023-01-13更新
|
1321次组卷
|
9卷引用:河北省保定市唐县第二中学2022-2023学年高二实验部下学期3月月考数学试题
河北省保定市唐县第二中学2022-2023学年高二实验部下学期3月月考数学试题安徽省宿州市泗县第一中学2022-2023学年高二上学期期末数学试题(已下线)安徽省江南十校2022届高三下学期3月一模理科数学试题变式题16-20(已下线)第七章 随机变量及其分布 讲核心 01(已下线)第七章 随机变量及其分布 讲核心 02(已下线)7.3.2离散型随机变量的方差(分层作业)山西省晋城市第一中学校2022-2023学年高二下学期4月第二次调研数学试题(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)【导学案】 3.2.4 离散型随机变量的方差 课前预习-湘教版(2019)选择性必修第二册 第3章 概率
解题方法
5 . 2017年8月8日晚我国四川九赛沟县发生了7.0级地震,为了解与掌握一些基本的地震安全防护知识,某小学在9月份开学初对全校学生进行了为期一周的知识讲座,事后并进行了测试(满分100分),根据测试成绩评定为“合格”(60分以上包含60分)、“不合格”两个等级,同时对相应等级进行量化:“合格”定为10分,“不合格”定为5分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
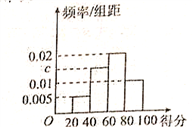
(1)求 ,
, ,
, 的值;
的值;
(2)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈,现再从这10人中任选4人,记所选4人的量化总分为 ,求
,求 的分布列及数学期望
的分布列及数学期望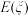 ;
;
(3)设函数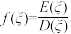 (其中
(其中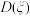 表示
表示 的方差)是评估安全教育方案成效的一种模拟函数,当
的方差)是评估安全教育方案成效的一种模拟函数,当 时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|

(1)求
 ,
, ,
, 的值;
的值;(2)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈,现再从这10人中任选4人,记所选4人的量化总分为
 ,求
,求 的分布列及数学期望
的分布列及数学期望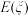 ;
;(3)设函数
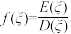 (其中
(其中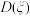 表示
表示 的方差)是评估安全教育方案成效的一种模拟函数,当
的方差)是评估安全教育方案成效的一种模拟函数,当 时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
时,认定教育方案是有效的;否则认定教育方案应需调整,试以此函数为参考依据.在(2)的条件下,判断该校是否应调整安全教育方案?
您最近一年使用:0次
解题方法
6 . 某校高二年级设计了一个实验学科的能力考查方案:考生从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.规定:至少正确完成其中2道题的便可通过该学科的能力考查.已知6道备选题中考生甲能正确完成其中4道题,另2道题不能完成;考生乙正确完成每道题的概率都为 .
.
(1)分别求考生甲、乙能通过该实验学科能力考查的概率;
(2)记所抽取的3道题中,考生甲能正确完成的题数为ξ,写出ξ的概率分布,并求 及
及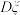 ;
;
(3)试用统计知识分析比较甲、乙考生在该实验学科上的能力水平.
 .
.(1)分别求考生甲、乙能通过该实验学科能力考查的概率;
(2)记所抽取的3道题中,考生甲能正确完成的题数为ξ,写出ξ的概率分布,并求
 及
及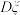 ;
;(3)试用统计知识分析比较甲、乙考生在该实验学科上的能力水平.
您最近一年使用:0次
2013·陕西西安·二模
7 . 某校设计了一个实验考查方案:考生从6道备选题中随机抽取3道题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中的2道题便可通过,已知6道备选题中考生甲有4道能正确完成,2道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的概率分布列,和甲、乙两考生的数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)求甲、乙两考生正确完成题数的概率分布列,和甲、乙两考生的数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
您最近一年使用:0次
2016-12-02更新
|
1655次组卷
|
4卷引用:河北省鹿泉县第一中学2018-2019学年高二5月月考数学(理)试题
河北省鹿泉县第一中学2018-2019学年高二5月月考数学(理)试题(已下线)2013届陕西长安一中等五校高三第二次模拟考试理科数学试卷福建省泉州市泉港区第一中学2018-2019学年高二下学期期中考数学(理)试题(已下线)2019年6月22日 《每日一题》理数(下学期期末复习)-周末培优