名校
解题方法
1 . 新冠疫情不断反弹,各大商超多措并举确保市民生活货品不断档,超市员工加班加点工作.某大型超市为答谢各位员工一年来的锐意进取和辛勤努力,拟在年会后,通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有5种面值奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2023-04-14更新
|
721次组卷
|
9卷引用:江苏省连云港高级中学2022-2023学年高二下学期期中数学试题
江苏省连云港高级中学2022-2023学年高二下学期期中数学试题山东省德州市2022-2023学年高二上学期期末数学试题(已下线)模块一 专题2 概率统计 (人教B)(已下线)模块三 专题5 概率与统计--拔高能力练(人教B版)福建省宁德市寿宁县第一中学2022-2023学年高二下学期第二阶段考试(5月)数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题03 条件概率与全概率公式(3)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(5)
2 . 在全球关注的抗击“新冠肺炎”中,某跨国科研中心的一个团队,研制了甲、乙两种治疗“新冠肺炎”新药,希望知道哪种新药更有效,为此进行动物试验,试验方案如下:
第一种:选取 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
第二种:选取 ,
, ,
, ,
, ,
, ,
, ,
,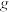 ,
, ,
, ,
, 共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,求其中服药有效的只数不超过2只的概率;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有90%变为正常白鼠,但正常白鼠仍有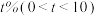 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为 .
.
(ⅰ)求 并写出
并写出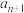 与
与 的关系式;
的关系式;
(ⅱ)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数 的值.
的值.
第一种:选取
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;第二种:选取
 ,
, ,
, ,
, ,
, ,
, ,
,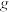 ,
, ,
, ,
, 共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,求其中服药有效的只数不超过2只的概率;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有90%变为正常白鼠,但正常白鼠仍有
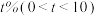 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为 .
.(ⅰ)求
 并写出
并写出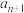 与
与 的关系式;
的关系式;(ⅱ)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数
 的值.
的值.
您最近一年使用:0次
解题方法
3 . 高二(16)班参加青华中学红五月节目:猜歌名,班级只有一个名额,结合平时观察积累,闫某峻,贾某轩两名学生进入最后选拔,申老师为此设计了如下选拔方案:挑选8首歌进行测试,在这8首歌曲中,闫某峻能正确说出其中的6首歌名,贾某轩能正确说出每首歌名的概率均为 ,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
(1)求闫某峻、贾某轩共答对3首歌名的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表高二(16)班参加红五月活动?
 ,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜
,假设闫某峻、贾某轩两名学生说出每首歌名都相互独立、互不影响,现闫某峻、贾某轩从这8首歌中分别随机抽取4首进行竞猜(1)求闫某峻、贾某轩共答对3首歌名的概率;
(2)从数学期望和方差的角度分析,应选拔哪个学生代表高二(16)班参加红五月活动?
您最近一年使用:0次
4 . 为推动党史学习教育工作扎实开展,营造“学党史、悟思想、办实事、开新局”的浓厚氛围,某校党委决定在教师党员中开展“学党史”知识竞赛.该校理综支部经过层层筛选,还有最后一个参赛名额要在甲,乙两名教师中间产生,支部书记设计了两种测试方案供两位教师选择.
方案一:从装有6个不同问题的纸盒中依次有放回抽取4个问题作答;
方案二:从装有6个不同问题的纸盒中依次不放回抽取4个问题作答.
已知这6个问题中,甲,乙两名教师都能正确回答其中的4个问题,且甲,乙两名教师对每个问题回答正确与否都是相互独立、互不影响的.假设甲教师选择了方案一,乙教师选择了方案二.
(1)求甲,乙两名教师都只答对2个问题的概率;
(2)若测试过程中每位教师答对1个问题得2分,答错得0分.你认为安排哪位教师参赛比较合适?请说明理由.
方案一:从装有6个不同问题的纸盒中依次有放回抽取4个问题作答;
方案二:从装有6个不同问题的纸盒中依次不放回抽取4个问题作答.
已知这6个问题中,甲,乙两名教师都能正确回答其中的4个问题,且甲,乙两名教师对每个问题回答正确与否都是相互独立、互不影响的.假设甲教师选择了方案一,乙教师选择了方案二.
(1)求甲,乙两名教师都只答对2个问题的概率;
(2)若测试过程中每位教师答对1个问题得2分,答错得0分.你认为安排哪位教师参赛比较合适?请说明理由.
您最近一年使用:0次
2024-03-29更新
|
1554次组卷
|
9卷引用:江苏省南通市2023-2024学年高二下学期3月质量监测数学试题
江苏省南通市2023-2024学年高二下学期3月质量监测数学试题(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)作业05 暑期培优必刷易错题-【暑假分层作业】(苏教版2019选择性必修第二册)(已下线)作业03 概率(2)-【暑假分层作业】(苏教版2019选择性必修第二册)(已下线)7.4.2超几何分布 第三练 能力提升拔高安徽省阜阳第一中学2023-2024学年高二下学期4月月考数学试题(已下线)专题3.3二项分布与超几何分布(六个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)河南省灵宝市第三高级中学2023-2024学年高二下学期精英对抗赛数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点1 重要的概率分布模型(一)【基础版】
名校
解题方法
5 . 我市拟建立一个博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标问题中随机抽取3个问题,已知这6个招标问题中,甲公司能正确回答其中4道题目,而乙公司能正确回答每道题目的概率均为  ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲公司至少答对2道题目的概率;
(2)分别求甲、乙两家公司答对题数的分布列,请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲公司至少答对2道题目的概率;
(2)分别求甲、乙两家公司答对题数的分布列,请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
您最近一年使用:0次
2024-05-31更新
|
1034次组卷
|
4卷引用:高二数学下学期期末押题--高二期末考点大串讲(苏教版2019选择性必修第二册)
(已下线)高二数学下学期期末押题--高二期末考点大串讲(苏教版2019选择性必修第二册)内蒙古自治区赤峰市红山区赤峰第四中学分校2023-2024学年高二下学期5月期中数学试题(已下线)专题04 随机变量及其分布类常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第二册)天津市第一中学2023-2024学年高二下学期期末质量调查数学试卷
6 . 某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道题进行测试,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
您最近一年使用:0次
2024-04-02更新
|
2609次组卷
|
10卷引用:江苏省扬州市仪征市精诚高级中学2023-2024学年高二下学期5月月考数学试题
江苏省扬州市仪征市精诚高级中学2023-2024学年高二下学期5月月考数学试题广东省东莞市东华高级中学2022-2023学年高二下学期期中考试数学试卷(已下线)高二下学期期中模拟卷(新题型)(导数+计数原理+随机变量及其分布+统计)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)吉林省长春市第五中学2023-2024年高二下学期第二学程数学试题四川省眉山市彭山区第一中学2023-2024学年高二下学期5月月考数学试题河北省承德市2023-2024学年高二年级下学期5月联考数学试题(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)四川省仁寿第一中学校(北校区)2023-2024学年高二下学期7月期末考试数学试题青海省西宁市海湖中学2023-2024学年高二下学期第二阶段考试数学试卷
解题方法
7 . 为了解学生中午的用餐方式(在食堂就餐或点外卖)与最近食堂间的距离的关系,某大学于某日中午随机调查了2000名学生,获得了如下频率分布表(不完整):
并且由该频率分布表,可估计学生与最近食堂间的平均距离为 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).
(1)补全频率分布表,并根据小概率值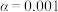 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过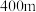 时,认为较近,否则认为较远):
时,认为较近,否则认为较远):
(2)已知该校李明同学的附近有两家学生食堂甲和乙,且他每天中午都选择食堂甲或乙就餐.
(i)一般情况下,学生更愿意去饭菜更美味的食堂就餐.某日中午,李明准备去食堂就餐.此时,记他选择去甲食堂就餐为事件 ,他认为甲食堂的饭菜比乙食堂的美味为事件
,他认为甲食堂的饭菜比乙食堂的美味为事件 ,且
,且 、
、 均为随机事件,证明:
均为随机事件,证明: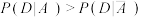 :
:
(ii)为迎接为期7天的校庆,甲食堂推出了如下两种优惠活动方案,顾客可任选其一.
①传统型优惠方案:校庆期间,顾客任意一天中午去甲食堂就餐均可获得 元优惠;
元优惠;
②“饥饿型”优惠方案:校庆期间,对于顾客去甲食堂就餐的若干天(不必连续)中午,第一天中午不优惠(即“饥饿”一天),第二天中午获得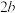 元优惠,以后每天中午均获得
元优惠,以后每天中午均获得 元优惠(其中
元优惠(其中 ,
, 为已知数且
为已知数且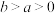 ).
).
校庆期间,已知李明每天中午去甲食堂就餐的概率均为 (
( ),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
附: ,其中
,其中 .
.
学生与最近食堂间的距离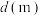 | 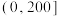 | 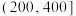 |  | 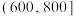 | 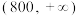 | 合计 |
| 在食堂就餐 | 0.15 | 0.10 | 0.00 | 0.50 | ||
| 点外卖 | 0.20 | 0.00 | 0.50 | |||
| 合计 | 0.20 | 0.15 | 0.00 | 1.00 |
 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).(1)补全频率分布表,并根据小概率值
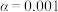 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过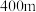 时,认为较近,否则认为较远):
时,认为较近,否则认为较远):(2)已知该校李明同学的附近有两家学生食堂甲和乙,且他每天中午都选择食堂甲或乙就餐.
(i)一般情况下,学生更愿意去饭菜更美味的食堂就餐.某日中午,李明准备去食堂就餐.此时,记他选择去甲食堂就餐为事件
 ,他认为甲食堂的饭菜比乙食堂的美味为事件
,他认为甲食堂的饭菜比乙食堂的美味为事件 ,且
,且 、
、 均为随机事件,证明:
均为随机事件,证明: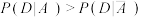 :
:(ii)为迎接为期7天的校庆,甲食堂推出了如下两种优惠活动方案,顾客可任选其一.
①传统型优惠方案:校庆期间,顾客任意一天中午去甲食堂就餐均可获得
 元优惠;
元优惠;②“饥饿型”优惠方案:校庆期间,对于顾客去甲食堂就餐的若干天(不必连续)中午,第一天中午不优惠(即“饥饿”一天),第二天中午获得
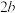 元优惠,以后每天中午均获得
元优惠,以后每天中午均获得 元优惠(其中
元优惠(其中 ,
, 为已知数且
为已知数且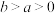 ).
).校庆期间,已知李明每天中午去甲食堂就餐的概率均为
 (
( ),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.附:
 ,其中
,其中 .
. | 0.10 | 0.010 | 0.001 |
 | 2.706 | 6.635 | 10.828 |
您最近一年使用:0次
2023-12-01更新
|
940次组卷
|
9卷引用:第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)福建省名校联盟2023届高三高考模拟考试4月数学试题(已下线)重难专攻(十三) 概率与统计的综合问题 B卷素养养成卷重庆市北碚区缙云教育联盟2024届高考零诊数学试题(已下线)专题05 成对数据的统计分析压轴题(3)(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)黄金卷06(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)专题4 独立性检验压轴大题(过关集训)
8 . 学校组织A,B,C,D,E五位同学参加某大学的测试活动,现有甲、乙两种不同的测试方案,每位同学随机选择其中的一种方案进行测试,选择甲方案测试合格的概率为 ,选择乙方案测试合格的概率为
,选择乙方案测试合格的概率为 ,且每位同学测试的结果互不影响.
,且每位同学测试的结果互不影响.
(1)若5位同学全选择甲方案,将测试合格的同学的人数记为X,求X的分布列及其方差;
(2)若测试合格的人数的期望值不小于3,求选择甲方案进行测试的同学的可能人数.
 ,选择乙方案测试合格的概率为
,选择乙方案测试合格的概率为 ,且每位同学测试的结果互不影响.
,且每位同学测试的结果互不影响.(1)若5位同学全选择甲方案,将测试合格的同学的人数记为X,求X的分布列及其方差;
(2)若测试合格的人数的期望值不小于3,求选择甲方案进行测试的同学的可能人数.
您最近一年使用:0次
名校
解题方法
9 . 为回馈顾客,某商场拟通过摸球兑奖的方式对500位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为45元,其余3个均为15元,求顾客所获的奖励额为60元的概率;
(2)商场对奖励总额的预算是30000元,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请从如下两种方案中选择一种,并说明理由.方案一:袋中的4个球由2个标有面值15元和2个标有面值45元的两种球组成;方案二:袋中的4个球由2个标有面值20元和2个标有面值40元的两种球组成.
(1)若袋中所装的4个球中有1个所标的面值为45元,其余3个均为15元,求顾客所获的奖励额为60元的概率;
(2)商场对奖励总额的预算是30000元,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请从如下两种方案中选择一种,并说明理由.方案一:袋中的4个球由2个标有面值15元和2个标有面值45元的两种球组成;方案二:袋中的4个球由2个标有面值20元和2个标有面值40元的两种球组成.
您最近一年使用:0次
2024-01-12更新
|
670次组卷
|
8卷引用:专题19 离散型随机变量及其分布列11种常见考法归类(3)
(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(3)重庆市黔江中学校2022届高三上学期8月考试数学试题广东省广州市仲元中学2024届高三第二次调研数学试题(已下线)专题03 条件概率与全概率公式(3)(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.3.2 离散型随机变量的方差——课后作业(巩固版)(已下线)第三章 随机变量及其分布列 专题二 随机变量的方差 微点2 随机变量的方差综合训练【培优版】
10 . 在做数学卷多选题时考生通常有以下两种策略:
策略A:为避免有选错得0分,在四个选项中只选出一个自己最有把握的选项,将多选题当作“单选题”来做,选对得2分;
策略B:争取得5分,选出自己认为正确的全部选项,漏选得2分,全部选对得5分.
本次期末考试前,某同学通过模拟训练得出其在两种策略下作完成下面小题的情况如下表:
已知该同学作答两题的状态互不影响,但这两题总耗时若超过10分钟,其它题目会因为时间紧张而少得1分.根据以上经验解答下列问题:
(1)若该同学此次考试决定用以下方案:第11题采用策略B,第12题采用策略A,设他这两题得分之和为X,求X的分布列、均值及方差;
(2)若该同学期望得到高分,请你替他设计答题方案.
策略A:为避免有选错得0分,在四个选项中只选出一个自己最有把握的选项,将多选题当作“单选题”来做,选对得2分;
策略B:争取得5分,选出自己认为正确的全部选项,漏选得2分,全部选对得5分.
本次期末考试前,某同学通过模拟训练得出其在两种策略下作完成下面小题的情况如下表:
策略 | 概率 | 每题耗时(分钟) | ||
第11题 | 第12题 | |||
A | 选对选项 | 0.8 | 0.5 | 3 |
B | 部分选对 | 0.6 | 0.2 | 6 |
全部选对 | 0.3 | 0.7 | ||
(1)若该同学此次考试决定用以下方案:第11题采用策略B,第12题采用策略A,设他这两题得分之和为X,求X的分布列、均值及方差;
(2)若该同学期望得到高分,请你替他设计答题方案.
您最近一年使用:0次
2022-07-01更新
|
1398次组卷
|
7卷引用:江苏省宿迁市2021-2022学年高二下学期期末数学试题
江苏省宿迁市2021-2022学年高二下学期期末数学试题【江苏专用】专题06概率与统计(第三部分)-高二下学期名校期末好题汇编(已下线)第四章 概率与统计(A卷·知识通关练)(3)(已下线)7.3.2离散型随机变量的方差(分层作业)辽宁省教研联盟2023届高三下学期第二次调研测试数学试题(已下线)专题7.3 离散型随机变量的数字特征【七大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)



