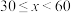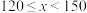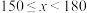2024高三·全国·专题练习
名校
1 . 某短视频软件经过几年的快速发展,深受人们的喜爱,该软件除了有娱乐属性外,也可通过平台推送广告.某公司为了宣传新产品,现有以下两种宣传方案:
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且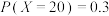 ,期望
,期望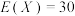 .
.
方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为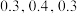 .
.
(1)请写出方案一的分布列,并求方差 ;
;
(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且
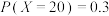 ,期望
,期望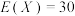 .
.方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为
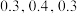 .
.(1)请写出方案一的分布列,并求方差
 ;
;(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
您最近一年使用:0次
2024-01-07更新
|
727次组卷
|
7卷引用:广东省东莞市七校2023-2024学年高二下学期5月联考数学试题
广东省东莞市七校2023-2024学年高二下学期5月联考数学试题(已下线)专题02 结论探索型【练】【北京版】(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题7.7 随机变量及其分布全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)陕西省咸阳市武功县普集高级中学2023-2024学年高二下学期6月月考数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)
2 . 某商场举行有奖促销活动,凡5月1日当天消费不低于1000元,均可抽奖一次,抽奖箱里有6个形状、大小、质地完全相同的小球,其中红球有4个,白球有2个,抽奖方案设置两种,顾客自行选择其中的一种方案.
方案一:从抽奖箱中,一次性摸出3个球,每有1个红球,可立减80元;
方案二:从抽奖箱中,有放回地每次摸出1个球,连摸3次,每摸到1次红球,立减80元.
(1)设方案一摸出的红球个数为随机变量X,求X的分布列、数学期望和方差;
(2)设方案二摸出的红球个数为随机变量Y,求Y的分布列、数学期望和方差;
(3)如果你是顾客,如何在上述两种抽奖方式中进行选择?请写出你的选择及简要理由.
方案一:从抽奖箱中,一次性摸出3个球,每有1个红球,可立减80元;
方案二:从抽奖箱中,有放回地每次摸出1个球,连摸3次,每摸到1次红球,立减80元.
(1)设方案一摸出的红球个数为随机变量X,求X的分布列、数学期望和方差;
(2)设方案二摸出的红球个数为随机变量Y,求Y的分布列、数学期望和方差;
(3)如果你是顾客,如何在上述两种抽奖方式中进行选择?请写出你的选择及简要理由.
您最近一年使用:0次
2024-07-16更新
|
149次组卷
|
3卷引用:广东省揭阳市2024-2025学年高三上学期9月月考数学试题
3 . 某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道题进行测试,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
 ,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答
,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量X,求X的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
您最近一年使用:0次
2024-04-02更新
|
2608次组卷
|
10卷引用:广东省东莞市东华高级中学2022-2023学年高二下学期期中考试数学试卷
广东省东莞市东华高级中学2022-2023学年高二下学期期中考试数学试卷(已下线)高二下学期期中模拟卷(新题型)(导数+计数原理+随机变量及其分布+统计)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)(已下线)第七章:随机变量及其分布章末重点题型复习(7题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)吉林省长春市第五中学2023-2024年高二下学期第二学程数学试题四川省眉山市彭山区第一中学2023-2024学年高二下学期5月月考数学试题河北省承德市2023-2024学年高二年级下学期5月联考数学试题(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)四川省仁寿第一中学校(北校区)2023-2024学年高二下学期7月期末考试数学试题青海省西宁市海湖中学2023-2024学年高二下学期第二阶段考试数学试卷江苏省扬州市仪征市精诚高级中学2023-2024学年高二下学期5月月考数学试题
名校
解题方法
4 . 为回馈顾客,某商场拟通过摸球兑奖的方式对500位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为45元,其余3个均为15元,求顾客所获的奖励额为60元的概率;
(2)商场对奖励总额的预算是30000元,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请从如下两种方案中选择一种,并说明理由.方案一:袋中的4个球由2个标有面值15元和2个标有面值45元的两种球组成;方案二:袋中的4个球由2个标有面值20元和2个标有面值40元的两种球组成.
(1)若袋中所装的4个球中有1个所标的面值为45元,其余3个均为15元,求顾客所获的奖励额为60元的概率;
(2)商场对奖励总额的预算是30000元,为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请从如下两种方案中选择一种,并说明理由.方案一:袋中的4个球由2个标有面值15元和2个标有面值45元的两种球组成;方案二:袋中的4个球由2个标有面值20元和2个标有面值40元的两种球组成.
您最近一年使用:0次
2024-01-12更新
|
670次组卷
|
8卷引用:广东省广州市仲元中学2024届高三第二次调研数学试题
广东省广州市仲元中学2024届高三第二次调研数学试题重庆市黔江中学校2022届高三上学期8月考试数学试题(已下线)专题19 离散型随机变量及其分布列11种常见考法归类(3)(已下线)专题03 条件概率与全概率公式(3)(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第05讲 7.3.2离散型随机变量的方差-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.3.2 离散型随机变量的方差——课后作业(巩固版)(已下线)第三章 随机变量及其分布列 专题二 随机变量的方差 微点2 随机变量的方差综合训练【培优版】
解题方法
5 . 为了解学生中午的用餐方式(在食堂就餐或点外卖)与最近食堂间的距离的关系,某大学于某日中午随机调查了2000名学生,获得了如下频率分布表(不完整):
并且由该频率分布表,可估计学生与最近食堂间的平均距离为 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).
(1)补全频率分布表,并根据小概率值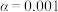 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过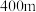 时,认为较近,否则认为较远):
时,认为较近,否则认为较远):
(2)已知该校李明同学的附近有两家学生食堂甲和乙,且他每天中午都选择食堂甲或乙就餐.
(i)一般情况下,学生更愿意去饭菜更美味的食堂就餐.某日中午,李明准备去食堂就餐.此时,记他选择去甲食堂就餐为事件 ,他认为甲食堂的饭菜比乙食堂的美味为事件
,他认为甲食堂的饭菜比乙食堂的美味为事件 ,且
,且 、
、 均为随机事件,证明:
均为随机事件,证明: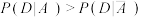 :
:
(ii)为迎接为期7天的校庆,甲食堂推出了如下两种优惠活动方案,顾客可任选其一.
①传统型优惠方案:校庆期间,顾客任意一天中午去甲食堂就餐均可获得 元优惠;
元优惠;
②“饥饿型”优惠方案:校庆期间,对于顾客去甲食堂就餐的若干天(不必连续)中午,第一天中午不优惠(即“饥饿”一天),第二天中午获得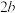 元优惠,以后每天中午均获得
元优惠,以后每天中午均获得 元优惠(其中
元优惠(其中 ,
, 为已知数且
为已知数且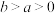 ).
).
校庆期间,已知李明每天中午去甲食堂就餐的概率均为 (
( ),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
附: ,其中
,其中 .
.
学生与最近食堂间的距离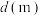 | 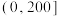 | 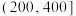 |  | 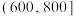 | 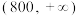 | 合计 |
| 在食堂就餐 | 0.15 | 0.10 | 0.00 | 0.50 | ||
| 点外卖 | 0.20 | 0.00 | 0.50 | |||
| 合计 | 0.20 | 0.15 | 0.00 | 1.00 |
 (同一组数据以该组数据所在区间的中点值作为代表).
(同一组数据以该组数据所在区间的中点值作为代表).(1)补全频率分布表,并根据小概率值
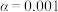 的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过
的独立性检验,能否认为学生中午的用餐方式与学生距最近食堂的远近有关(当学生与最近食堂间的距离不超过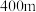 时,认为较近,否则认为较远):
时,认为较近,否则认为较远):(2)已知该校李明同学的附近有两家学生食堂甲和乙,且他每天中午都选择食堂甲或乙就餐.
(i)一般情况下,学生更愿意去饭菜更美味的食堂就餐.某日中午,李明准备去食堂就餐.此时,记他选择去甲食堂就餐为事件
 ,他认为甲食堂的饭菜比乙食堂的美味为事件
,他认为甲食堂的饭菜比乙食堂的美味为事件 ,且
,且 、
、 均为随机事件,证明:
均为随机事件,证明: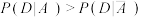 :
:(ii)为迎接为期7天的校庆,甲食堂推出了如下两种优惠活动方案,顾客可任选其一.
①传统型优惠方案:校庆期间,顾客任意一天中午去甲食堂就餐均可获得
 元优惠;
元优惠;②“饥饿型”优惠方案:校庆期间,对于顾客去甲食堂就餐的若干天(不必连续)中午,第一天中午不优惠(即“饥饿”一天),第二天中午获得
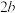 元优惠,以后每天中午均获得
元优惠,以后每天中午均获得 元优惠(其中
元优惠(其中 ,
, 为已知数且
为已知数且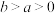 ).
).校庆期间,已知李明每天中午去甲食堂就餐的概率均为
 (
( ),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.
),且是否去甲食堂就餐相互独立.又知李明是一名“激进型”消费者,如果两种方案获得的优惠期望不一样,他倾向于选择能获得优惠期望更大的方案,如果两种方案获得的优惠期望一样,他倾向于选择获得的优惠更分散的方案.请你据此帮他作出选择,并说明理由.附:
 ,其中
,其中 .
. | 0.10 | 0.010 | 0.001 |
 | 2.706 | 6.635 | 10.828 |
您最近一年使用:0次
2023-12-01更新
|
940次组卷
|
9卷引用:黄金卷06
(已下线)黄金卷06福建省名校联盟2023届高三高考模拟考试4月数学试题(已下线)重难专攻(十三) 概率与统计的综合问题 B卷素养养成卷重庆市北碚区缙云教育联盟2024届高考零诊数学试题(已下线)专题05 成对数据的统计分析压轴题(3)(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)专题4 独立性检验压轴大题(过关集训)
名校
6 . 甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从 道备选题中一次性随机抽取
道备选题中一次性随机抽取 道题,按照答对题目的个数为标准进行筛选.已知
道题,按照答对题目的个数为标准进行筛选.已知 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成, 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列;
(2)请从均值和方差的角度分析比较甲、乙两人谁的面试通过的可能性较大?
 道备选题中一次性随机抽取
道备选题中一次性随机抽取 道题,按照答对题目的个数为标准进行筛选.已知
道题,按照答对题目的个数为标准进行筛选.已知 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成, 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列;
(2)请从均值和方差的角度分析比较甲、乙两人谁的面试通过的可能性较大?
您最近一年使用:0次
2023-06-24更新
|
939次组卷
|
7卷引用:广东省珠海市香樟中学2022-2023学年高二下学期6月月考数学试题
广东省珠海市香樟中学2022-2023学年高二下学期6月月考数学试题广东省江门市新会第一中学等2023-2024学年高二下学期5月联考数学试题山东省临沂市2022-2023学年高二下学期期中数学试题(已下线)模块一 专题7 区分超几何分布与二项分布问题(已下线)考点巩固卷26分布列及三大分布(十一大考点)-2吉林省延边第二中学2023-2024学年高二上学期第二次阶段检测数学试卷(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)
名校
7 . 某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标问题中随机抽取3个问题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正确回答每道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(1)求甲、乙两家公司共答对2道题目的概率;
(2)设甲公司答对题数为随机变量 ,求
,求 的分布列、数学期望和方差;
的分布列、数学期望和方差;
(3)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲、乙两家公司共答对2道题目的概率;
(2)设甲公司答对题数为随机变量
 ,求
,求 的分布列、数学期望和方差;
的分布列、数学期望和方差;(3)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
您最近一年使用:0次
2023-04-02更新
|
2207次组卷
|
14卷引用:广东省广州一中2023-2024学年高二下学期期中数学试题
广东省广州一中2023-2024学年高二下学期期中数学试题山西省太原市第五中学2022-2023学年高二下学期3月月考数学试题黑龙江省哈尔滨德强学校2022-2023学年高二下学期3月月考数学试题A新疆乌鲁木齐市第四中学2022-2023学年高二上学期期中阶段诊断测试数学试题(已下线)高二数学下学期期中模拟试题01(数列、导数、计数原理)广西百色市2022-2023学年高二下学期期末教学质量调研数学试题河南省周口市沈丘县长安高级中学2022-2023学年高二下学期期中考试数学试题福建省泉州现代中学2022-2023学年高二下学期期中考试数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)(已下线)艺体生一轮复习 第九章 计数原理、概率与统计 第47讲 离散型随机变量的均值与方差【练】(已下线)专题7.3 离散型随机变量的数字特征【七大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)河南省南阳市第一中学校2023-2024学年高二下学期开学考试数学试题(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)(已下线)第三章 随机变量及其分布列 专题四 随机变量分布列、期望、方差的应用 微点4 概率分布在生活、生产实践中的应用(四)【培优版】
8 . 为迎接党的“二十大”胜利召开,学校计划组织党史知识竞赛.某班设计一个预选方案:选手从6道题中随机抽取3道进行回答.已知甲6道题中会4道,乙每道题答对的概率都是 ,且每道题答对与否互不影响.
,且每道题答对与否互不影响.
(1)分别求出甲、乙两人答对题数的概率分布列;
(2)你认为派谁参加知识竞赛更合适,请说明你的理由.
 ,且每道题答对与否互不影响.
,且每道题答对与否互不影响.(1)分别求出甲、乙两人答对题数的概率分布列;
(2)你认为派谁参加知识竞赛更合适,请说明你的理由.
您最近一年使用:0次
2022-07-18更新
|
1079次组卷
|
8卷引用:广东省广州市白云中学2024届高三上学期9月考试数学试题
广东省广州市白云中学2024届高三上学期9月考试数学试题黑龙江省齐齐哈尔市2021-2022学年高二下学期期末数学试题(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)河南省南阳市第一中学校2022-2023学年高二上学期12月月考数学试题(已下线)第七章 随机变量及其分布 讲核心 02(已下线)7.4.1二项分布(精讲)黑龙江省宾县第二中学2023-2024学年高三上学期期初学业质量检测数学试题(已下线)第七章 随机变量及其分布 讲核心 02
名校
解题方法
9 . 已知袋中装有大小相同的2个白球和4个红球,现在采取两种不同的方案取出球,具体如下:
(1)从袋中随机地取出一个球,放回后再随机地取出一个球,这样连续取4次球,求共取得红球次数 的分布列;
的分布列;
(2)从袋中随机地将球逐个取出,每次取后不放回,直到取出两个红球为止,求取球次数 的数学期望和方差.
的数学期望和方差.
(1)从袋中随机地取出一个球,放回后再随机地取出一个球,这样连续取4次球,求共取得红球次数
 的分布列;
的分布列;(2)从袋中随机地将球逐个取出,每次取后不放回,直到取出两个红球为止,求取球次数
 的数学期望和方差.
的数学期望和方差.
您最近一年使用:0次
2022-06-22更新
|
420次组卷
|
2卷引用:广东省中山市迪茵公学2021-2022学年高二下学期第二次月考数学试题
10 . 某校为了提升学生的科学素养、本学期初开始动员学生利用课外时间阅读科普读物、为了了解学生平均每周课外阅读科普读物所花的时间、学期末该校通过简单随机抽样的方法收集了20名学生平均每周课外阅读的时间(分钟)的数据、得到如表统计表(设 表示阅读时间,单位:分钟)
表示阅读时间,单位:分钟)
(1)完成下面的 列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?
列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?
附: .
.
(2)为了选出1名选手代表学校参加全市中小学生科普知识比赛,学校组织了考组对选手人选进行考核,经过层层筛选,甲、乙两名学生成为进入最后阶段的备选选手.考核组设计了最终确定人选的方案:请甲、乙两名学生从6道试题中随机抽取3道试题作答,已知这6道试题中,甲可正确回答其中的4道题目,而乙能正确回答每道题目的概率均为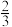 ,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
 表示阅读时间,单位:分钟)
表示阅读时间,单位:分钟)组别 | 时间分组 | 频数 | 男生人数 | 女生人数 |
1 |
| 2 | 1 | 1 |
2 |
| 10 | 4 | 6 |
3 |
| 4 | 3 | 1 |
4 |
| 2 | 1 | 1 |
5 |
| 2 | 2 | 0 |
 列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?
列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?平均每周阅读时间不少于120分钟 | 平均每周阅读时间少于120分钟 | 合计 | |
男 | |||
女 | |||
合计 |
 .
.
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
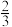 ,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
您最近一年使用:0次
2021-08-25更新
|
322次组卷
|
2卷引用:广东省韶关市2020-2021学年高二下学期期末数学试题