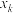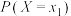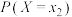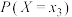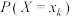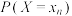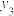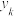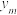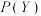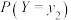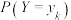名校
解题方法
1 . 设离散型随机变量X,Y的取值分别为 ,
,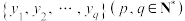 .定义X关于事件“
.定义X关于事件“ ”
”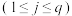 的条件数学期望为
的条件数学期望为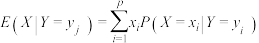 ,已知条件数学期望满足全期望公式
,已知条件数学期望满足全期望公式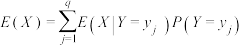 .解决如下问题:为了研究某药物对于微生物A生存状况的影响,某实验室计划进行生物实验.在第1天上午,实验人员向培养皿中加入10个A的个体.从第1天开始,实验人员在每天下午向培养皿中加入该种药物.当加入药物时,A的每个个体立即产生1次如下的生理反应(设A的每个个体在当天的其他时刻均不发生变化,不同个体的生理反应相互独立):①直接死亡;②分裂为2个个体,且这两种生理反应是等可能的.
.解决如下问题:为了研究某药物对于微生物A生存状况的影响,某实验室计划进行生物实验.在第1天上午,实验人员向培养皿中加入10个A的个体.从第1天开始,实验人员在每天下午向培养皿中加入该种药物.当加入药物时,A的每个个体立即产生1次如下的生理反应(设A的每个个体在当天的其他时刻均不发生变化,不同个体的生理反应相互独立):①直接死亡;②分裂为2个个体,且这两种生理反应是等可能的.
设第n天上午培养皿中A的个体数量为 .规定
.规定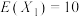 ,
,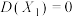 .
.
(1)求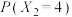 ,
,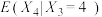 ;
;
(2)证明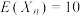 ;
;
(3)已知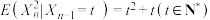 ,求
,求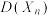 ,并结合(2)说明其实际含义.
,并结合(2)说明其实际含义.
附:对于随机变量X, .
.
 ,
,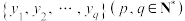 .定义X关于事件“
.定义X关于事件“ ”
”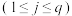 的条件数学期望为
的条件数学期望为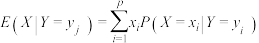 ,已知条件数学期望满足全期望公式
,已知条件数学期望满足全期望公式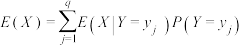 .解决如下问题:为了研究某药物对于微生物A生存状况的影响,某实验室计划进行生物实验.在第1天上午,实验人员向培养皿中加入10个A的个体.从第1天开始,实验人员在每天下午向培养皿中加入该种药物.当加入药物时,A的每个个体立即产生1次如下的生理反应(设A的每个个体在当天的其他时刻均不发生变化,不同个体的生理反应相互独立):①直接死亡;②分裂为2个个体,且这两种生理反应是等可能的.
.解决如下问题:为了研究某药物对于微生物A生存状况的影响,某实验室计划进行生物实验.在第1天上午,实验人员向培养皿中加入10个A的个体.从第1天开始,实验人员在每天下午向培养皿中加入该种药物.当加入药物时,A的每个个体立即产生1次如下的生理反应(设A的每个个体在当天的其他时刻均不发生变化,不同个体的生理反应相互独立):①直接死亡;②分裂为2个个体,且这两种生理反应是等可能的.设第n天上午培养皿中A的个体数量为
 .规定
.规定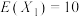 ,
,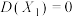 .
.(1)求
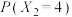 ,
,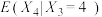 ;
;(2)证明
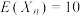 ;
;(3)已知
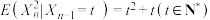 ,求
,求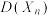 ,并结合(2)说明其实际含义.
,并结合(2)说明其实际含义.附:对于随机变量X,
 .
.
您最近一年使用:0次
7日内更新
|
142次组卷
|
2卷引用:2024届福建省莆田市第一中学高三下学期5月模拟考试数学试题
名校
解题方法
2 . 在三维空间中,单位立方体的顶点坐标可用三维坐标 表示,其中
表示,其中 .而在
.而在 维空间中
维空间中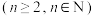 ,以单位立方体的顶点坐标可表示为
,以单位立方体的顶点坐标可表示为 维坐标
维坐标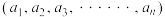 ,其中
,其中 .现有如下定义:在
.现有如下定义:在 维空间中,
维空间中,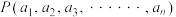 ,
,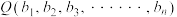 两点的曼哈顿距离为
两点的曼哈顿距离为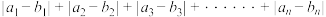
(1)在3维单位立方体中任取两个不同顶点,试求所取两点的曼哈顿距离为1的概率;
(2)在 维单位立方体中任取两个不同顶点,记随机变量
维单位立方体中任取两个不同顶点,记随机变量 为所取两点间的曼哈顿距离
为所取两点间的曼哈顿距离
(i)求出 的分布列与期望;
的分布列与期望;
(ii)证明:随机变量 的方差小于
的方差小于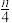 .
.
 表示,其中
表示,其中 .而在
.而在 维空间中
维空间中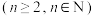 ,以单位立方体的顶点坐标可表示为
,以单位立方体的顶点坐标可表示为 维坐标
维坐标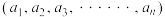 ,其中
,其中 .现有如下定义:在
.现有如下定义:在 维空间中,
维空间中,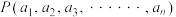 ,
,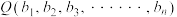 两点的曼哈顿距离为
两点的曼哈顿距离为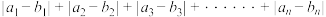
(1)在3维单位立方体中任取两个不同顶点,试求所取两点的曼哈顿距离为1的概率;
(2)在
 维单位立方体中任取两个不同顶点,记随机变量
维单位立方体中任取两个不同顶点,记随机变量 为所取两点间的曼哈顿距离
为所取两点间的曼哈顿距离(i)求出
 的分布列与期望;
的分布列与期望;(ii)证明:随机变量
 的方差小于
的方差小于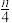 .
.
您最近一年使用:0次
名校
解题方法
3 . 在三维空间中,立方体的坐标可用三维坐标 表示,其中
表示,其中 ,而在
,而在 维空间中
维空间中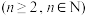 ,以单位长度为边长的“立方体”的顶点坐标可表示为
,以单位长度为边长的“立方体”的顶点坐标可表示为 维坐标
维坐标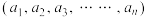 ,其中
,其中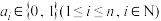 .现有如下定义:在
.现有如下定义:在 维空间中两点间的曼哈顿距离为两点
维空间中两点间的曼哈顿距离为两点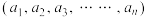 与
与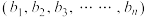 坐标差的绝对值之和,即为
坐标差的绝对值之和,即为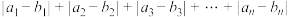 .回答下列问题:
.回答下列问题:
(1)求出 维“立方体”的顶点数;
维“立方体”的顶点数;
(2)在 维“立方体”中任取两个不同顶点,记随机变量
维“立方体”中任取两个不同顶点,记随机变量 为所取两点间的曼哈顿距离.
为所取两点间的曼哈顿距离.
①求 的分布列与期望;
的分布列与期望;
②求 的方差.
的方差.
 表示,其中
表示,其中 ,而在
,而在 维空间中
维空间中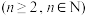 ,以单位长度为边长的“立方体”的顶点坐标可表示为
,以单位长度为边长的“立方体”的顶点坐标可表示为 维坐标
维坐标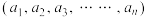 ,其中
,其中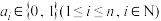 .现有如下定义:在
.现有如下定义:在 维空间中两点间的曼哈顿距离为两点
维空间中两点间的曼哈顿距离为两点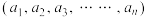 与
与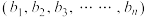 坐标差的绝对值之和,即为
坐标差的绝对值之和,即为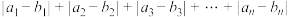 .回答下列问题:
.回答下列问题:(1)求出
 维“立方体”的顶点数;
维“立方体”的顶点数;(2)在
 维“立方体”中任取两个不同顶点,记随机变量
维“立方体”中任取两个不同顶点,记随机变量 为所取两点间的曼哈顿距离.
为所取两点间的曼哈顿距离.①求
 的分布列与期望;
的分布列与期望;②求
 的方差.
的方差.
您最近一年使用:0次
2024-06-11更新
|
539次组卷
|
3卷引用:江西省新八校2024届高三第二次联考数学试题
4 . 组合投资需要同时考虑风险与收益.为了控制风险需要组合低风险资产,为了扩大收益需要组合高收益资产,现有两个相互独立的投资项目A和B,单独投资100万元项目A的收益记为随机变量X,单独投资100万元项目B的收益记为随机变量Y.若将100万资金按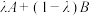 进行组合投资,则投资收益的随机变量Z满足
进行组合投资,则投资收益的随机变量Z满足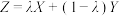 ,其中
,其中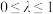 .假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
.假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
(1)若 ,
, ,求Z的期望与方差;
,求Z的期望与方差;
(2)已知随机变量X满足分布列:
随机变量Y满足分布列:
且随机变量X与Y相互独立,即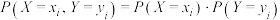 ,
,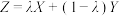 ,
,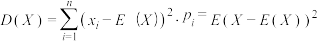 .求证:
.求证: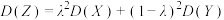 ;
;
(3)若投资项目X是高收益资产,其每年的收益满足:有30%的可能亏损当前资产的一半;有70%的可能增值当前资产的一倍.投资项目 是低风险资产,满足
是低风险资产,满足 .试问
.试问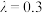 能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
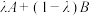 进行组合投资,则投资收益的随机变量Z满足
进行组合投资,则投资收益的随机变量Z满足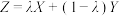 ,其中
,其中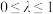 .假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.
.假设在组合投资中,可用随机变量的期望衡量收益,可用随机变量的方差衡量风险.(1)若
 ,
, ,求Z的期望与方差;
,求Z的期望与方差;(2)已知随机变量X满足分布列:
X |
|
|
| … |
| … |
|
|
|
|
| … |
| … |
|
Y |
|
|
| … |
| … |
|
|
|
|
| … |
| … |
|
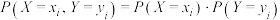 ,
,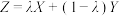 ,
,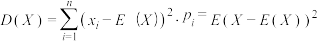 .求证:
.求证: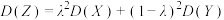 ;
;(3)若投资项目X是高收益资产,其每年的收益满足:有30%的可能亏损当前资产的一半;有70%的可能增值当前资产的一倍.投资项目
 是低风险资产,满足
是低风险资产,满足 .试问
.试问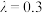 能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
能否满足投资第1年的收益不低于17万,风险不高于500?请说明理由.
您最近一年使用:0次
名校
解题方法
5 . 某自然保护区经过几十年的发展,某种濒临灭绝动物数量有大幅度的增加.已知这种动物 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物
种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物 ,统计其中
,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第
种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量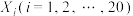 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 (
( ,
, 均大于100),每一次试验均相互独立.
均大于100),每一次试验均相互独立.
(1)求 的分布列;
的分布列;
(2)记随机变量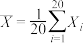 .已知
.已知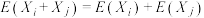 ,
,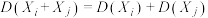
(i)证明: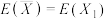 ,
,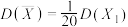 ;
;
(ii)该小组完成所有试验后,得到 的实际取值分别为
的实际取值分别为 .数据
.数据 的平均值
的平均值 ,方差
,方差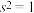 .采用
.采用 和
和 分别代替
分别代替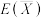 和
和 ,给出
,给出 ,
, 的估计值.
的估计值.
(已知随机变量 服从超几何分布记为:
服从超几何分布记为: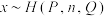 (其中
(其中 为总数,
为总数, 为某类元素的个数,
为某类元素的个数, 为抽取的个数),则
为抽取的个数),则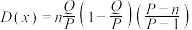 )
)
 拥有两个亚种(分别记为
拥有两个亚种(分别记为 种和
种和 种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物
种).为了调查该区域中这两个亚种的数目,某动物研究小组计划在该区域中捕捉100个动物 ,统计其中
,统计其中 种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第
种的数目后,将捕获的动物全部放回,作为一次试验结果.重复进行这个试验共20次,记第 次试验中
次试验中 种的数目为随机变量
种的数目为随机变量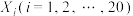 .设该区域中
.设该区域中 种的数目为
种的数目为 ,
, 种的数目为
种的数目为 (
( ,
, 均大于100),每一次试验均相互独立.
均大于100),每一次试验均相互独立.(1)求
 的分布列;
的分布列;(2)记随机变量
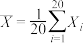 .已知
.已知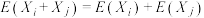 ,
,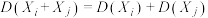
(i)证明:
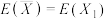 ,
,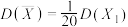 ;
;(ii)该小组完成所有试验后,得到
 的实际取值分别为
的实际取值分别为 .数据
.数据 的平均值
的平均值 ,方差
,方差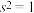 .采用
.采用 和
和 分别代替
分别代替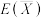 和
和 ,给出
,给出 ,
, 的估计值.
的估计值.(已知随机变量
 服从超几何分布记为:
服从超几何分布记为: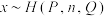 (其中
(其中 为总数,
为总数, 为某类元素的个数,
为某类元素的个数, 为抽取的个数),则
为抽取的个数),则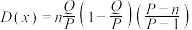 )
)
您最近一年使用:0次
2024-04-24更新
|
1644次组卷
|
3卷引用:2024届辽宁省辽宁省高三重点高中协作校联考模拟预测数学试题
6 . 某区域中的物种C有A种和B种两个亚种.为了调查该区域中这两个亚种的数目比例(A种数目比B种数目少),某生物研究小组设计了如下实验方案:①在该区域中有放回的捕捉50个物种C,统计其中A种数目,以此作为一次试验的结果;②重复进行这个试验n次(其中 ),记第i次试验中的A种数目为随机变量
),记第i次试验中的A种数目为随机变量 (
(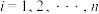 );③记随机变量
);③记随机变量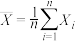 ,利用
,利用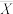 的期望
的期望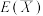 和方差
和方差 进行估算.设该区域中A种数目为M,B种数目为N,每一次试验都相互独立.
进行估算.设该区域中A种数目为M,B种数目为N,每一次试验都相互独立.
(1)已知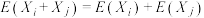 ,
,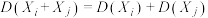 ,证明:
,证明: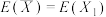 ,
,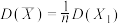 ;
;
(2)该小组完成所有试验后,得到 的实际取值分别为
的实际取值分别为 (
(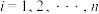 ),并计算了数据
),并计算了数据 (
(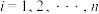 )的平均值
)的平均值 和方差
和方差 ,然后部分数据丢失,仅剩方差的数据
,然后部分数据丢失,仅剩方差的数据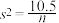 .
.
(ⅰ)请用 和
和 分别代替
分别代替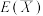 和
和 ,估算
,估算 和
和 ;
;
(ⅱ)在(ⅰ)的条件下,求 的分布列中概率值最大的随机事件
的分布列中概率值最大的随机事件 对应的随机变量的取值.
对应的随机变量的取值.
 ),记第i次试验中的A种数目为随机变量
),记第i次试验中的A种数目为随机变量 (
(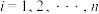 );③记随机变量
);③记随机变量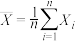 ,利用
,利用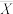 的期望
的期望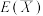 和方差
和方差 进行估算.设该区域中A种数目为M,B种数目为N,每一次试验都相互独立.
进行估算.设该区域中A种数目为M,B种数目为N,每一次试验都相互独立.(1)已知
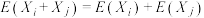 ,
,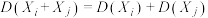 ,证明:
,证明: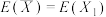 ,
,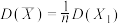 ;
;(2)该小组完成所有试验后,得到
 的实际取值分别为
的实际取值分别为 (
(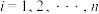 ),并计算了数据
),并计算了数据 (
(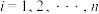 )的平均值
)的平均值 和方差
和方差 ,然后部分数据丢失,仅剩方差的数据
,然后部分数据丢失,仅剩方差的数据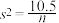 .
.(ⅰ)请用
 和
和 分别代替
分别代替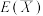 和
和 ,估算
,估算 和
和 ;
;(ⅱ)在(ⅰ)的条件下,求
 的分布列中概率值最大的随机事件
的分布列中概率值最大的随机事件 对应的随机变量的取值.
对应的随机变量的取值.
您最近一年使用:0次
2024-01-18更新
|
1062次组卷
|
8卷引用:广东省东莞市2024届高三上学期期末数学试题
广东省东莞市2024届高三上学期期末数学试题(已下线)专题04 超几何分布+二项分布+正态分布压轴题(2)(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)模块八 概率与统计(测试)(已下线)第06讲 7.4.1二项分布-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)第七章 概率初步(续)(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)(已下线)7.4.1 二项分布——课后作业(巩固版)
名校
7 . 人口老龄化加剧的背景下,我国先后颁布了一系列生育政策,根据不同政策要求,分为两个时期Ⅰ和Ⅱ.根据部分调查数据总结出如下规律:对于同一个家庭,在Ⅰ时期内生孩 人,在Ⅱ时期生孩
人,在Ⅱ时期生孩 人,(不考虑多胞胎)生男生女的概率相等.
人,(不考虑多胞胎)生男生女的概率相等. 服从0-1分布且
服从0-1分布且 .
. 分布列如下图:
分布列如下图:
现已知一个家庭在Ⅰ时期没生孩子,则在Ⅱ时期生2个孩子概率为 ;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为
;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为 ;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为
;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为 ,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为
,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为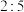 (针对普遍家庭).
(针对普遍家庭).
(1)求 的期望与方差;
的期望与方差;
(2)由数据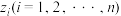 组成的样本空间根据分层随机抽样分为两层,样本点之比为
组成的样本空间根据分层随机抽样分为两层,样本点之比为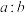 ,分别为
,分别为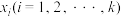 与
与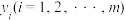 ,
,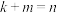 ,总体样本点与两个分层样本点均值分别为
,总体样本点与两个分层样本点均值分别为 ,
, ,
,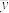 ,方差分别为
,方差分别为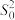 ,
,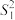 ,
,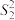 ,证明:
,证明: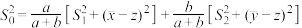 ,并利用该公式估算题设样本总体的方差.
,并利用该公式估算题设样本总体的方差.
 人,在Ⅱ时期生孩
人,在Ⅱ时期生孩 人,(不考虑多胞胎)生男生女的概率相等.
人,(不考虑多胞胎)生男生女的概率相等. 服从0-1分布且
服从0-1分布且 .
. 分布列如下图:
分布列如下图: | 0 | 1 | 2 |
 |  |  |  |
 ;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为
;若在Ⅰ时期生了1个女孩,则在时期生2个孩子概率为 ;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为
;若在Ⅰ时期生了1个男孩,则在Ⅱ时期生2个孩子概率为 ,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为
,样本点中Ⅰ时期生孩人数与Ⅱ时期生孩人数之比为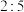 (针对普遍家庭).
(针对普遍家庭).(1)求
 的期望与方差;
的期望与方差;(2)由数据
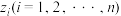 组成的样本空间根据分层随机抽样分为两层,样本点之比为
组成的样本空间根据分层随机抽样分为两层,样本点之比为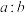 ,分别为
,分别为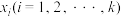 与
与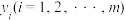 ,
,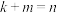 ,总体样本点与两个分层样本点均值分别为
,总体样本点与两个分层样本点均值分别为 ,
, ,
,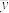 ,方差分别为
,方差分别为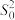 ,
,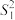 ,
,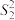 ,证明:
,证明: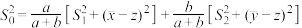 ,并利用该公式估算题设样本总体的方差.
,并利用该公式估算题设样本总体的方差.
您最近一年使用:0次
2023-08-02更新
|
1195次组卷
|
8卷引用:浙江省名校联盟2022-2023学年高二下学期期末联考数学试题
浙江省名校联盟2022-2023学年高二下学期期末联考数学试题广东省深圳市宝安区2024届高三上学期10月调研数学试题湖北省武昌实验中学2023-2024学年高三上学期10月月考数学试题(已下线)第二节 用样本的数字特征估计总体 B卷素养养成卷 一轮复习点点通(已下线)专题03 条件概率与全概率公式(4)(已下线)高二下学期期末数学试卷(巩固篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)重庆市第一中学校2023-2024学年高二下学期5月月考数学试题(已下线)专题02概率统计期末10种常考题型归类【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(人教B版2019选择性必修第二册)
8 . 为切实做好新冠疫情防控工作,有效、及时地控制和消除新冠肺炎的危害,增加学生对新冠肺炎预防知识的了解,某校举办了一次“新冠疫情”知识竞赛.竞赛分个人赛和团体赛两种.个人赛参赛方式为:组委会采取电脑出题的方式,从题库中随机出10道题,编号为 ,
, ,
, ,
, ,
, ,
,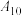 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
方案一:将班级选派的 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.
方案二:将班级选派的 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
 ,
, ,
, ,
, ,
, ,
,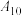 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:方案一:将班级选派的
 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.方案二:将班级选派的
 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为
 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数
 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
您最近一年使用:0次
9 . 中国男子篮球职业联赛(CBA)始于1995年,至今已有28个赛季,根据传统,在每个赛季总决赛之后,要举办一场南北对抗的全明星比赛,其中三分王的投球环节最为吸引眼球,三分王投球的比赛规则如下:一共有五个不同角度的三分点位,每个三分点位有5个球(前四个是普通球,最后一个球是花球),前四个球每投中一个得1分,投不中的得0分,最后一个花球投中得2分,投不中得0分.全明星参赛球员甲在第一个角度的三分点开始投球,已知球员甲投球的命中率为 ,且每次投篮是否命中相互独立.
,且每次投篮是否命中相互独立.
(1)记球员甲投完1个普通球的得分为X,求X的方差D(X);
(2)若球员甲投完第一个三分点位的5个球后共得到了2分,求他是投中了花球而得到了2分的概率;
(3)在比赛结束后与球迷的互动环节中,将球员甲在前两个三分点位使用过的10个篮球对应的小模型放入箱中,由幸运球迷从箱中随机摸出5个小模型,并规定,摸出一个花球小模型计2分,摸出一个普通球小模型计1分,求该幸运球迷摸出5个小模型后的总计分Y的数学期望.
 ,且每次投篮是否命中相互独立.
,且每次投篮是否命中相互独立.(1)记球员甲投完1个普通球的得分为X,求X的方差D(X);
(2)若球员甲投完第一个三分点位的5个球后共得到了2分,求他是投中了花球而得到了2分的概率;
(3)在比赛结束后与球迷的互动环节中,将球员甲在前两个三分点位使用过的10个篮球对应的小模型放入箱中,由幸运球迷从箱中随机摸出5个小模型,并规定,摸出一个花球小模型计2分,摸出一个普通球小模型计1分,求该幸运球迷摸出5个小模型后的总计分Y的数学期望.
您最近一年使用:0次
2022-07-14更新
|
2039次组卷
|
11卷引用:辽宁省丹东市2021-2022学年高二下学期期末数学试题
辽宁省丹东市2021-2022学年高二下学期期末数学试题重庆市缙云教育联盟2023届高三上学期8月质量检测数学试题(已下线)第四章 概率与统计(A卷·知识通关练)(3)(已下线)7.4.2超几何分布(分层作业)-【上好课】2022-2023学年高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)7.4.2 超几何分布 (精练)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)(已下线)7.4 二项分布与超几何分布(练习)-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)8.2.3-8.2.4二项分布 超几何分布(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)(已下线)8.2.4超几何分布(2)辽宁省辽宁师范大学附属中学2023年高三下学期5月月考数学试题吉林省长春市十一高中2022-2023学年高二下学期期末数学试题(已下线)专题02 高二下期末真题精选(压轴题 )-高二期末考点大串讲(人教A版2019)
10 . 在做数学卷多选题时考生通常有以下两种策略:
策略A:为避免有选错得0分,在四个选项中只选出一个自己最有把握的选项,将多选题当作“单选题”来做,选对得2分;
策略B:争取得5分,选出自己认为正确的全部选项,漏选得2分,全部选对得5分.
本次期末考试前,某同学通过模拟训练得出其在两种策略下作完成下面小题的情况如下表:
已知该同学作答两题的状态互不影响,但这两题总耗时若超过10分钟,其它题目会因为时间紧张而少得1分.根据以上经验解答下列问题:
(1)若该同学此次考试决定用以下方案:第11题采用策略B,第12题采用策略A,设他这两题得分之和为X,求X的分布列、均值及方差;
(2)若该同学期望得到高分,请你替他设计答题方案.
策略A:为避免有选错得0分,在四个选项中只选出一个自己最有把握的选项,将多选题当作“单选题”来做,选对得2分;
策略B:争取得5分,选出自己认为正确的全部选项,漏选得2分,全部选对得5分.
本次期末考试前,某同学通过模拟训练得出其在两种策略下作完成下面小题的情况如下表:
策略 | 概率 | 每题耗时(分钟) | ||
第11题 | 第12题 | |||
A | 选对选项 | 0.8 | 0.5 | 3 |
B | 部分选对 | 0.6 | 0.2 | 6 |
全部选对 | 0.3 | 0.7 | ||
(1)若该同学此次考试决定用以下方案:第11题采用策略B,第12题采用策略A,设他这两题得分之和为X,求X的分布列、均值及方差;
(2)若该同学期望得到高分,请你替他设计答题方案.
您最近一年使用:0次
2022-07-01更新
|
1346次组卷
|
7卷引用:江苏省宿迁市2021-2022学年高二下学期期末数学试题
江苏省宿迁市2021-2022学年高二下学期期末数学试题(已下线)第四章 概率与统计(A卷·知识通关练)(3)(已下线)7.3.2离散型随机变量的方差(分层作业)-【上好课】2022-2023学年高二数学同步备课系列(人教A版2019选择性必修第三册)辽宁省教研联盟2023届高三下学期第二次调研测试数学试题(已下线)专题7.3 离散型随机变量的数字特征【七大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)【江苏专用】专题06概率与统计(第三部分)-高二下学期名校期末好题汇编