2024·安徽·二模
1 . 在平面直角坐标系 中,利用公式
中,利用公式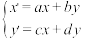 ①(其中
①(其中 ,
, ,
, ,
, 为常数),将点
为常数),将点 变换为点
变换为点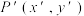 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由
的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 ,
, ,
, ,
, 组成的正方形数表
组成的正方形数表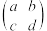 唯一确定,我们将
唯一确定,我们将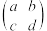 称为二阶矩阵,矩阵通常用大写英文字母
称为二阶矩阵,矩阵通常用大写英文字母 ,
, ,…表示.
,…表示. 中,将点
中,将点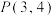 绕原点
绕原点 按逆时针旋转
按逆时针旋转 得到点
得到点 (到原点距离不变),求点
(到原点距离不变),求点 的坐标;
的坐标;
(2)如图,在平面直角坐标系 中,将点
中,将点 绕原点
绕原点 按逆时针旋转
按逆时针旋转 角得到点
角得到点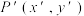 (到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(3)向量 (称为行向量形式),也可以写成
(称为行向量形式),也可以写成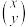 ,这种形式的向量称为列向量,线性变换坐标公式①可以表示为:
,这种形式的向量称为列向量,线性变换坐标公式①可以表示为: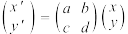 ,则称
,则称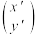 是二阶矩阵
是二阶矩阵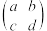 与向量
与向量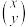 的乘积,设
的乘积,设 是一个二阶矩阵,
是一个二阶矩阵,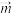 ,
, 是平面上的任意两个向量,求证:
是平面上的任意两个向量,求证: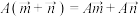 .
.
 中,利用公式
中,利用公式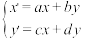 ①(其中
①(其中 ,
, ,
, ,
, 为常数),将点
为常数),将点 变换为点
变换为点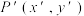 的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由
的坐标,我们称该变换为线性变换,也称①为坐标变换公式,该变换公式①可由 ,
, ,
, ,
, 组成的正方形数表
组成的正方形数表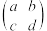 唯一确定,我们将
唯一确定,我们将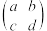 称为二阶矩阵,矩阵通常用大写英文字母
称为二阶矩阵,矩阵通常用大写英文字母 ,
, ,…表示.
,…表示.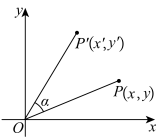
 中,将点
中,将点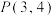 绕原点
绕原点 按逆时针旋转
按逆时针旋转 得到点
得到点 (到原点距离不变),求点
(到原点距离不变),求点 的坐标;
的坐标;(2)如图,在平面直角坐标系
 中,将点
中,将点 绕原点
绕原点 按逆时针旋转
按逆时针旋转 角得到点
角得到点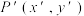 (到原点距离不变),求坐标变换公式及对应的二阶矩阵;
(到原点距离不变),求坐标变换公式及对应的二阶矩阵;(3)向量
 (称为行向量形式),也可以写成
(称为行向量形式),也可以写成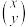 ,这种形式的向量称为列向量,线性变换坐标公式①可以表示为:
,这种形式的向量称为列向量,线性变换坐标公式①可以表示为: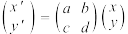 ,则称
,则称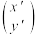 是二阶矩阵
是二阶矩阵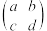 与向量
与向量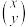 的乘积,设
的乘积,设 是一个二阶矩阵,
是一个二阶矩阵,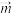 ,
, 是平面上的任意两个向量,求证:
是平面上的任意两个向量,求证: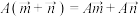 .
.
您最近半年使用:0次
名校
2 . 设数阵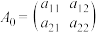 ,其中
,其中 、
、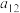 、
、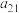 、
、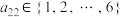 .设
.设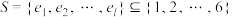 ,其中
,其中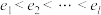 ,
, 且
且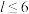 .定义变换
.定义变换 为“对于数阵的每一行,若其中有
为“对于数阵的每一行,若其中有 或
或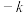 ,则将这一行中每个数都乘以
,则将这一行中每个数都乘以 ;若其中没有
;若其中没有 且没有
且没有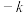 ,则这一行中所有数均保持不变”(
,则这一行中所有数均保持不变”( 、
、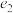 、
、 、
、 ).
).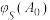 表示“将
表示“将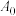 经过
经过 变换得到
变换得到 ,再将
,再将 经过
经过 变换得到
变换得到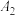 、
、 ,以此类推,最后将
,以此类推,最后将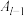 经过
经过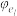 变换得到
变换得到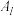 ”,记数阵
”,记数阵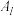 中四个数的和为
中四个数的和为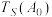 .
.
(1)若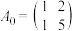 ,写出
,写出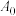 经过
经过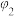 变换后得到的数阵
变换后得到的数阵 ;
;
(2)若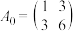 ,
, ,求
,求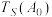 的值;
的值;
(3)对任意确定的一个数阵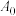 ,证明:
,证明: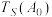 的所有可能取值的和不超过
的所有可能取值的和不超过 .
.
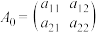 ,其中
,其中 、
、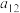 、
、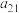 、
、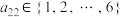 .设
.设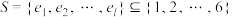 ,其中
,其中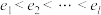 ,
, 且
且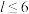 .定义变换
.定义变换 为“对于数阵的每一行,若其中有
为“对于数阵的每一行,若其中有 或
或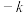 ,则将这一行中每个数都乘以
,则将这一行中每个数都乘以 ;若其中没有
;若其中没有 且没有
且没有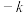 ,则这一行中所有数均保持不变”(
,则这一行中所有数均保持不变”( 、
、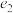 、
、 、
、 ).
).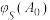 表示“将
表示“将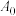 经过
经过 变换得到
变换得到 ,再将
,再将 经过
经过 变换得到
变换得到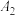 、
、 ,以此类推,最后将
,以此类推,最后将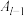 经过
经过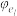 变换得到
变换得到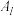 ”,记数阵
”,记数阵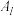 中四个数的和为
中四个数的和为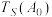 .
.(1)若
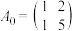 ,写出
,写出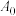 经过
经过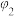 变换后得到的数阵
变换后得到的数阵 ;
;(2)若
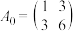 ,
, ,求
,求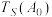 的值;
的值;(3)对任意确定的一个数阵
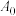 ,证明:
,证明: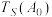 的所有可能取值的和不超过
的所有可能取值的和不超过 .
.
您最近半年使用:0次
2020-04-16更新
|
454次组卷
|
5卷引用:北京市第十二中学2020-2021学年高一3月月考数学试题
名校
解题方法
3 . 定义 ,则
,则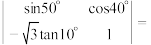 ( )
( )
 ,则
,则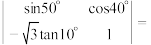 ( )
( )A. | B. | C. | D. |
您最近半年使用:0次



