名校
解题方法
1 . 已知椭圆 :
:
 的离心率为
的离心率为 ,长轴的右端点为
,长轴的右端点为 .
.
(1)求 的方程;
的方程;
(2)直线 与椭圆
与椭圆 分别相交于
分别相交于 两点,且
两点,且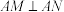 ,点
,点 不在直线
不在直线 上.
上.
①试证明直线 过一定点,并求出此定点;
过一定点,并求出此定点;
②从点 作
作 垂足为
垂足为 ,点
,点 ,写出
,写出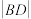 的最小值(结论不要求证明).
的最小值(结论不要求证明).
 :
:
 的离心率为
的离心率为 ,长轴的右端点为
,长轴的右端点为 .
.(1)求
 的方程;
的方程;(2)直线
 与椭圆
与椭圆 分别相交于
分别相交于 两点,且
两点,且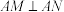 ,点
,点 不在直线
不在直线 上.
上.①试证明直线
 过一定点,并求出此定点;
过一定点,并求出此定点;②从点
 作
作 垂足为
垂足为 ,点
,点 ,写出
,写出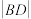 的最小值(结论不要求证明).
的最小值(结论不要求证明).
您最近一年使用:0次
2022-04-01更新
|
788次组卷
|
3卷引用:北京市门头沟区2022届高三一模数学试题
名校
解题方法
2 . 已知椭圆 过点
过点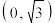 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线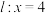 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)求证:直线 与
与 的斜率之积为定值;
的斜率之积为定值;
(3)判断三点 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
 过点
过点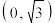 ,且离心率为
,且离心率为 .设
.设 ,
, 为椭圆
为椭圆 的左、右顶点,
的左、右顶点, 为椭圆上异于
为椭圆上异于 ,
, 的一点,直线
的一点,直线 ,
, 分别与直线
分别与直线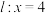 相交于
相交于 ,
, 两点,且直线
两点,且直线 与椭圆
与椭圆 交于另一点
交于另一点 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)求证:直线
 与
与 的斜率之积为定值;
的斜率之积为定值;(3)判断三点
 ,
, ,
, 是否共线:并证明你的结论.
是否共线:并证明你的结论.
您最近一年使用:0次
2022-10-11更新
|
1672次组卷
|
9卷引用:【区级联考】北京市昌平区2019届高三第一学期期末数学(文)试题
解题方法
3 . 用光线照射物体,在某个平面上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面.由平行光线形成的投影叫做平行投影,由点光源发出的光线形成的投影叫做中心投影.投影线垂直于投影面产生的平行投影叫做正投影,投影线不垂直于投影而产生的平行投影叫做斜投影.物体投影的形状、大小与它相对于投影面的位置和角度有关.如图所示,已知平行四边形 在平面
在平面 内的平行投影是四边形
内的平行投影是四边形 .
.
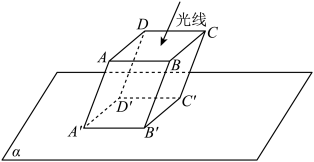
(1)若平行四边形 平行于投影面(如图
平行于投影面(如图 ),求证:四边形
),求证:四边形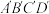 是平行四边形;
是平行四边形;
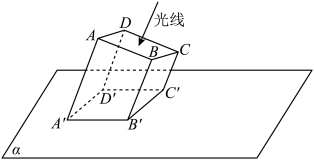
(2)在图 中作出平面
中作出平面 与平面
与平面 的交线(保留作图痕迹,不需要写出过程);
的交线(保留作图痕迹,不需要写出过程);
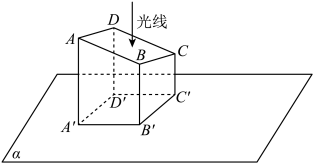
(3)如图 ,已知四边形
,已知四边形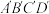 和平行四边形
和平行四边形 的面积分别为
的面积分别为 ,平面
,平面 与平面
与平面 的交线是直线
的交线是直线 ,且这个平行投影是正投影.设二面角
,且这个平行投影是正投影.设二面角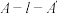 的平面角为
的平面角为 (
( 为锐角),猜想并写出角
为锐角),猜想并写出角 的余弦值(用
的余弦值(用 表示),再给出证明.
表示),再给出证明.
 在平面
在平面 内的平行投影是四边形
内的平行投影是四边形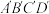 .
.
图

图

图
(1)若平行四边形
 平行于投影面(如图
平行于投影面(如图 ),求证:四边形
),求证:四边形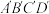 是平行四边形;
是平行四边形;(2)在图
 中作出平面
中作出平面 与平面
与平面 的交线(保留作图痕迹,不需要写出过程);
的交线(保留作图痕迹,不需要写出过程);(3)如图
 ,已知四边形
,已知四边形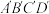 和平行四边形
和平行四边形 的面积分别为
的面积分别为 ,平面
,平面 与平面
与平面 的交线是直线
的交线是直线 ,且这个平行投影是正投影.设二面角
,且这个平行投影是正投影.设二面角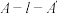 的平面角为
的平面角为 (
( 为锐角),猜想并写出角
为锐角),猜想并写出角 的余弦值(用
的余弦值(用 表示),再给出证明.
表示),再给出证明.
您最近一年使用:0次
名校
4 . 设A为非空集合,令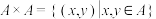 ,则
,则 的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如
的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如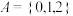 时,
时,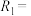 {0,2},
{0,2},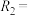
 ,
, ,
,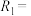 {(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:
{(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:
①(自反性)若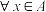 ,有
,有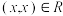 ,则称R在A上是自反的;
,则称R在A上是自反的;
②(对称性)若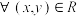 ,有
,有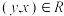 ,则称R在A上是对称的;
,则称R在A上是对称的;
③(传递性)若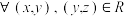 ,有
,有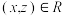 ,则称R在A上是传递的;
,则称R在A上是传递的;
如果R同时满足这3条性质,则称R为A上的等价关系.
(1)已知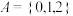 ,按要求填空:
,按要求填空:
①用列举法写出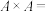 ______________________;
______________________;
②A上的关系有____________个(用数值做答);
③用列举法写出A上的所有等价关系:{(0,0),(1,1),(2,2)},{(0,0),(1,1),(2,2),(0,1),(1,0)},{(0,0),(1,1),(2,2),(0,2),(2,0)},_______________,_______________,共5个.
(2)设 和
和 是某个非空集合A上的关系,证明:
是某个非空集合A上的关系,证明:
①若 ,
, 是自反的和对称的,则
是自反的和对称的,则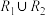 也是自反的和对称的;
也是自反的和对称的;
②若 ,
, 是传递的,则
是传递的,则 也是传递的.
也是传递的.
(3)若给定的集合A有n个元素( ),
), ,
, ,...,
,..., 为A的非空子集,满足
为A的非空子集,满足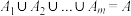 且两两交集为空集.求证:
且两两交集为空集.求证: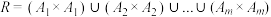 为A上的等价关系.
为A上的等价关系.
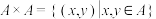 ,则
,则 的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如
的任意子集R都叫做从A到A的一个关系(Relation),简称A上的关系.例如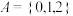 时,
时,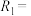 {0,2},
{0,2},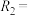
 ,
, ,
,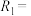 {(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:
{(0,0),(2,1)}等都是A上的关系.设R为非空集合A上的关系.给出如下定义:①(自反性)若
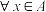 ,有
,有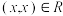 ,则称R在A上是自反的;
,则称R在A上是自反的;②(对称性)若
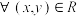 ,有
,有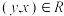 ,则称R在A上是对称的;
,则称R在A上是对称的;③(传递性)若
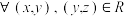 ,有
,有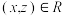 ,则称R在A上是传递的;
,则称R在A上是传递的;如果R同时满足这3条性质,则称R为A上的等价关系.
(1)已知
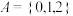 ,按要求填空:
,按要求填空:①用列举法写出
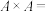 ______________________;
______________________;②A上的关系有____________个(用数值做答);
③用列举法写出A上的所有等价关系:{(0,0),(1,1),(2,2)},{(0,0),(1,1),(2,2),(0,1),(1,0)},{(0,0),(1,1),(2,2),(0,2),(2,0)},_______________,_______________,共5个.
(2)设
 和
和 是某个非空集合A上的关系,证明:
是某个非空集合A上的关系,证明:①若
 ,
, 是自反的和对称的,则
是自反的和对称的,则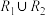 也是自反的和对称的;
也是自反的和对称的;②若
 ,
, 是传递的,则
是传递的,则 也是传递的.
也是传递的.(3)若给定的集合A有n个元素(
 ),
), ,
, ,...,
,..., 为A的非空子集,满足
为A的非空子集,满足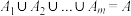 且两两交集为空集.求证:
且两两交集为空集.求证: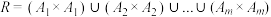 为A上的等价关系.
为A上的等价关系.
您最近一年使用:0次
名校
解题方法
5 . 设函数 的定义域为
的定义域为 .若存在常数
.若存在常数 ,
, ,使得对于任意
,使得对于任意 ,
, 成立,则称函数
成立,则称函数 具有性质
具有性质 .
.
(1)判断函数 和
和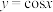 具有性质
具有性质 ?(结论不要求证明)
?(结论不要求证明)
(2)若函数 具有性质
具有性质 ,且其对应的
,且其对应的 ,
, .已知当
.已知当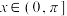 时,
时,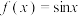 ,求函数
,求函数 在区间
在区间 上的最大值;
上的最大值;
(3)若函数 具有性质
具有性质 ,且直线
,且直线 为其图像的一条对称轴,证明:
为其图像的一条对称轴,证明: 为周期函数.
为周期函数.
 的定义域为
的定义域为 .若存在常数
.若存在常数 ,
, ,使得对于任意
,使得对于任意 ,
, 成立,则称函数
成立,则称函数 具有性质
具有性质 .
.(1)判断函数
 和
和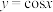 具有性质
具有性质 ?(结论不要求证明)
?(结论不要求证明)(2)若函数
 具有性质
具有性质 ,且其对应的
,且其对应的 ,
, .已知当
.已知当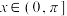 时,
时,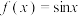 ,求函数
,求函数 在区间
在区间 上的最大值;
上的最大值;(3)若函数
 具有性质
具有性质 ,且直线
,且直线 为其图像的一条对称轴,证明:
为其图像的一条对称轴,证明: 为周期函数.
为周期函数.
您最近一年使用:0次
2021-08-01更新
|
568次组卷
|
3卷引用:北京市西城区2020-2021学年高一下学期期末数学试题
名校
解题方法
6 . 已知函数 .
.
(1)求证:当 时,
时,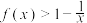 ;
;
(2)设斜率为 的直线与曲线
的直线与曲线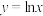 交于两点
交于两点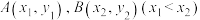 ,证明:
,证明: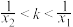 .
.
 .
.(1)求证:当
 时,
时,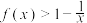 ;
;(2)设斜率为
 的直线与曲线
的直线与曲线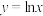 交于两点
交于两点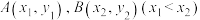 ,证明:
,证明: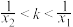 .
.
您最近一年使用:0次
2021-08-04更新
|
665次组卷
|
3卷引用:北京市大兴区2020-2021学年高二下学期期末数学试题
北京市大兴区2020-2021学年高二下学期期末数学试题安徽省六安市舒城中学2022届高三下学期一模理科数学试题(已下线)湖北省武汉市(武汉六中)部分重点中学2024届高三第二次联考数学试题变式题17-22
名校
7 . 设函数 的定义域为R.若存在常数
的定义域为R.若存在常数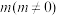 ,对于任意
,对于任意 ,
, 成立,则称函数
成立,则称函数 具有性质
具有性质 .记P为满足性质
.记P为满足性质 的所有函数的集合.
的所有函数的集合.
(I)判断函数 和
和 是否属于集合P?(结论不要求证明)
是否属于集合P?(结论不要求证明)
(II)若函数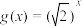 ,证明:
,证明: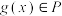 ;
;
(III)记二次函数的全体为集合 ,证明:
,证明: .
.
 的定义域为R.若存在常数
的定义域为R.若存在常数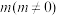 ,对于任意
,对于任意 ,
, 成立,则称函数
成立,则称函数 具有性质
具有性质 .记P为满足性质
.记P为满足性质 的所有函数的集合.
的所有函数的集合.(I)判断函数
 和
和 是否属于集合P?(结论不要求证明)
是否属于集合P?(结论不要求证明)(II)若函数
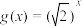 ,证明:
,证明: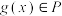 ;
;(III)记二次函数的全体为集合
 ,证明:
,证明: .
.
您最近一年使用:0次
2021-01-26更新
|
703次组卷
|
3卷引用:北京市西城区2020-2021学年高一上学期期末考试数学试题
8 . 设数集 满足:①任意
满足:①任意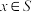 ,有
,有 ;②任意
;②任意 、
、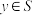 ,有
,有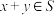 或
或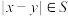 ,则称数集
,则称数集 具有性质
具有性质 .
.
(1)判断数集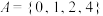 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(2)若数集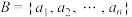 且
且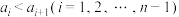 具有性质
具有性质 .
.
(i)当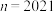 时,求证:
时,求证: 、
、 、
、 、
、 是等差数列;
是等差数列;
(ii)当 、
、 、
、 、
、 不是等差数列时,写出
不是等差数列时,写出 的最大值.(结论不需要证明)
的最大值.(结论不需要证明)
 满足:①任意
满足:①任意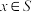 ,有
,有 ;②任意
;②任意 、
、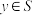 ,有
,有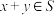 或
或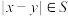 ,则称数集
,则称数集 具有性质
具有性质 .
.(1)判断数集
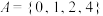 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(2)若数集
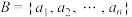 且
且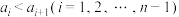 具有性质
具有性质 .
.(i)当
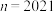 时,求证:
时,求证: 、
、 、
、 、
、 是等差数列;
是等差数列;(ii)当
 、
、 、
、 、
、 不是等差数列时,写出
不是等差数列时,写出 的最大值.(结论不需要证明)
的最大值.(结论不需要证明)
您最近一年使用:0次
2021-09-26更新
|
582次组卷
|
7卷引用:北京市丰台区2021届高三二模数学试题
名校
9 . 已知M是由满足下述条件的函数构成的集合:对任意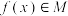 ,①方程
,①方程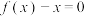 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足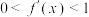 .
.
(1)判断函数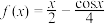 是集合M中的元素,并说明理由;
是集合M中的元素,并说明理由;
(2)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意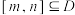 ,都存在
,都存在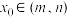 ,使得等式
,使得等式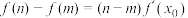 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程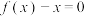 有且只有一个实数根;
有且只有一个实数根;
(3)对任意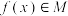 ,且
,且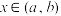 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
, ,当
,当 ,且
,且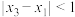 时,
时,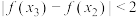 .
.
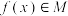 ,①方程
,①方程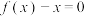 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足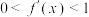 .
.(1)判断函数
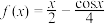 是集合M中的元素,并说明理由;
是集合M中的元素,并说明理由;(2)集合M中的元素
 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意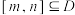 ,都存在
,都存在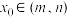 ,使得等式
,使得等式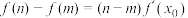 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程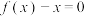 有且只有一个实数根;
有且只有一个实数根;(3)对任意
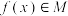 ,且
,且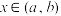 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
, ,当
,当 ,且
,且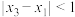 时,
时,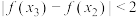 .
.
您最近一年使用:0次
10 . 若有穷数列 满足
满足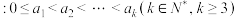 且对任意的
且对任意的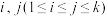 ,
, 至少有一个是数列
至少有一个是数列 中的项,则称数列
中的项,则称数列 具有性质
具有性质
(1)判断数列1,2,4,8是否具有性质P,并说明理由;
(2)设项数为 的数列
的数列 具有性质
具有性质 ,求证:
,求证: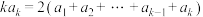 ;
;
(3)若项数为 的数列
的数列 具有性质
具有性质 ,写出一个当
,写出一个当 时,
时, 不是等差数列的例子,并证明当
不是等差数列的例子,并证明当 时,数列
时,数列 是等差数列
是等差数列
 满足
满足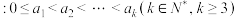 且对任意的
且对任意的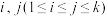 ,
, 至少有一个是数列
至少有一个是数列 中的项,则称数列
中的项,则称数列 具有性质
具有性质
(1)判断数列1,2,4,8是否具有性质P,并说明理由;
(2)设项数为
 的数列
的数列 具有性质
具有性质 ,求证:
,求证: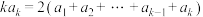 ;
;(3)若项数为
 的数列
的数列 具有性质
具有性质 ,写出一个当
,写出一个当 时,
时, 不是等差数列的例子,并证明当
不是等差数列的例子,并证明当 时,数列
时,数列 是等差数列
是等差数列
您最近一年使用:0次
2020-12-25更新
|
586次组卷
|
6卷引用:北京市第五十五中学2022-2023年高二下学期3月调研数学试题
北京市第五十五中学2022-2023年高二下学期3月调研数学试题上海市嘉定区2021届高三上学期一模数学试题(已下线)重难点01 数列(基本通项求法)-2021年高考数学【热点·重点·难点】专练(上海专用)(已下线)考向17 数列新定义-备战2022年高考数学一轮复习考点微专题(上海专用)(已下线)专题05 《数列》中的解答题压轴题(2)-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)(已下线)上海高二下学期期末真题精选(压轴60题35个考点专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)



