名校
解题方法
1 . 已知定义域为 的偶函数
的偶函数 满足
满足 ,当
,当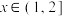 时
时 ,则下列结论正确的有( )
,则下列结论正确的有( )
 的偶函数
的偶函数 满足
满足 ,当
,当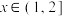 时
时 ,则下列结论正确的有( )
,则下列结论正确的有( )A. |
B. 的图象关于点 的图象关于点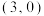 成中心对称 成中心对称 |
C. |
D.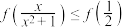 |
您最近一年使用:0次
2024-09-04更新
|
1618次组卷
|
6卷引用:河南省安阳市林州市第一中学2025届高三上学期10月调研考试数学试题
名校
解题方法
2 . 已知公比为 的等比数列
的等比数列 满足
满足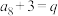 ,且
,且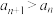 ,则
,则 的取值范围为
的取值范围为________ .
 的等比数列
的等比数列 满足
满足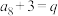 ,且
,且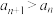 ,则
,则 的取值范围为
的取值范围为
您最近一年使用:0次
名校
解题方法
3 . 已知函数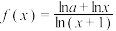 .
.
(1)求 的定义域;
的定义域;
(2)若 存在极大值,求
存在极大值,求 的取值范围
的取值范围
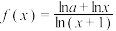 .
.(1)求
 的定义域;
的定义域;(2)若
 存在极大值,求
存在极大值,求 的取值范围
的取值范围
您最近一年使用:0次
名校
解题方法
4 . 在空间直角坐标系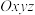 中,过点
中,过点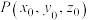 且以
且以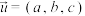 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为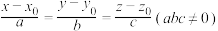 ,过点
,过点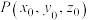 且以
且以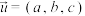 为法向量的平面方程可表示为
为法向量的平面方程可表示为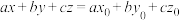 .
.
(1)若直线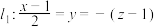 与
与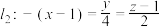 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;
(2)在三棱柱 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面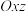 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;
(3)若集合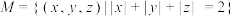 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
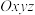 中,过点
中,过点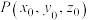 且以
且以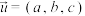 为方向向量的直线方程可表示为
为方向向量的直线方程可表示为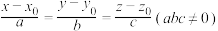 ,过点
,过点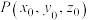 且以
且以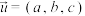 为法向量的平面方程可表示为
为法向量的平面方程可表示为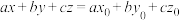 .
.(1)若直线
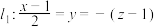 与
与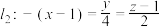 都在平面
都在平面 内,求平面
内,求平面 的方程;
的方程;(2)在三棱柱
 中,点
中,点 与坐标原点
与坐标原点 重合,点
重合,点 在平面
在平面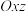 内,平面
内,平面 以
以 为法向量,平面
为法向量,平面 的方程为
的方程为 ,求点
,求点 的坐标;
的坐标;(3)若集合
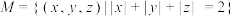 中所有的点构成了多面体
中所有的点构成了多面体 的各个面,求
的各个面,求 的体积和相邻两个面所在平面的夹角的余弦值.
的体积和相邻两个面所在平面的夹角的余弦值.
您最近一年使用:0次
解题方法
5 . 已知函数 与
与 的定义域的交集为
的定义域的交集为 .若
.若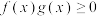 对
对 恒成立,则称
恒成立,则称 与
与 为同号函数,例如
为同号函数,例如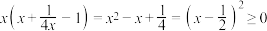 ,则函数
,则函数 与
与 为同号函数.若存在区间
为同号函数.若存在区间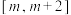 ,使得
,使得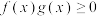 对
对 恒成立,则称
恒成立,则称 与
与 为区间同号函数.
为区间同号函数.
(1)设函数 ,试问这三个函数中是否任意两个都互为区间同号函数?请说明你的理由.
,试问这三个函数中是否任意两个都互为区间同号函数?请说明你的理由.
(2)设函数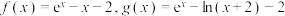 .
.
(ⅰ)证明: 与
与 为同号函数.
为同号函数.
(ⅱ)若 恒成立,证明:
恒成立,证明: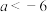 .
.
 与
与 的定义域的交集为
的定义域的交集为 .若
.若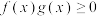 对
对 恒成立,则称
恒成立,则称 与
与 为同号函数,例如
为同号函数,例如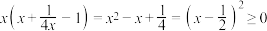 ,则函数
,则函数 与
与 为同号函数.若存在区间
为同号函数.若存在区间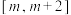 ,使得
,使得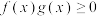 对
对 恒成立,则称
恒成立,则称 与
与 为区间同号函数.
为区间同号函数.(1)设函数
 ,试问这三个函数中是否任意两个都互为区间同号函数?请说明你的理由.
,试问这三个函数中是否任意两个都互为区间同号函数?请说明你的理由.(2)设函数
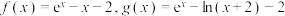 .
.(ⅰ)证明:
 与
与 为同号函数.
为同号函数.(ⅱ)若
 恒成立,证明:
恒成立,证明: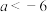 .
.
您最近一年使用:0次
6 . 已知函数 ,下列说法正确的是( )
,下列说法正确的是( )
 ,下列说法正确的是( )
,下列说法正确的是( )A.当 时,函数 时,函数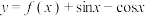 的值域是 的值域是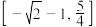 |
B.将 图象的横坐标缩短为原来的 图象的横坐标缩短为原来的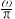 ,纵坐标不变,得到函数 ,纵坐标不变,得到函数 的图象,则函数 的图象,则函数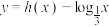 有3个零点 有3个零点 |
C.若函数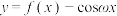 在区间 在区间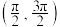 内没有零点,则 内没有零点,则 的取值范围为 的取值范围为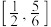 |
D.若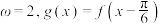 ,记方程 ,记方程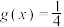 在 在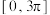 上的根从小到大依次为 上的根从小到大依次为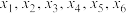 ,则 ,则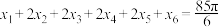 |
您最近一年使用:0次
解题方法
7 . 函数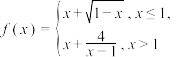 的值域为( )
的值域为( )
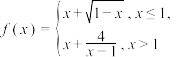 的值域为( )
的值域为( )A.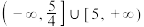 | B.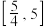 |
C.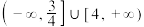 | D.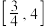 |
您最近一年使用:0次
名校
8 . 已知曲线 上有不同的两点
上有不同的两点 和
和 ,若点
,若点 关于直线
关于直线 的对称点
的对称点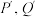 在曲线
在曲线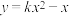 上,则实数
上,则实数 的取值范围为
的取值范围为_____________ .
 上有不同的两点
上有不同的两点 和
和 ,若点
,若点 关于直线
关于直线 的对称点
的对称点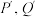 在曲线
在曲线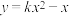 上,则实数
上,则实数 的取值范围为
的取值范围为
您最近一年使用:0次
7日内更新
|
211次组卷
|
3卷引用:河南省部分名校2024-2025学年高三上学期阶段性测试(二)数学试题
名校
解题方法
9 . 已知对任意 ,不等式
,不等式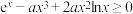 恒成立,则实数
恒成立,则实数 的可能取值为( )
的可能取值为( )
 ,不等式
,不等式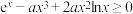 恒成立,则实数
恒成立,则实数 的可能取值为( )
的可能取值为( )| A.1 | B.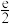 | C.e | D.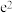 |
您最近一年使用:0次
7日内更新
|
264次组卷
|
2卷引用:河南省部分名校2024-2025学年高三上学期阶段性测试(二)数学试题
名校
10 . 已知函数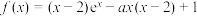 .
.
(1)若 仅有一个极值点且
仅有一个极值点且 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 变化时,求
变化时,求 的图象经过的所有定点的坐标,并请写出一个函数
的图象经过的所有定点的坐标,并请写出一个函数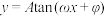 ,使其图象经过上述所有定点;
,使其图象经过上述所有定点;
(3)证明: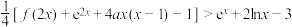 .
.
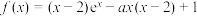 .
.(1)若
 仅有一个极值点且
仅有一个极值点且 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(2)当
 变化时,求
变化时,求 的图象经过的所有定点的坐标,并请写出一个函数
的图象经过的所有定点的坐标,并请写出一个函数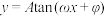 ,使其图象经过上述所有定点;
,使其图象经过上述所有定点;(3)证明:
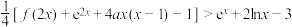 .
.
您最近一年使用:0次
7日内更新
|
224次组卷
|
2卷引用:河南省部分名校2024-2025学年高三上学期阶段性测试(二)数学试题



