1 . 对于任意正整数n,进行如下操作:若n为偶数,则对n不断地除以2,直到得到一个奇数,记这个奇数为 ;若n为奇数,则对
;若n为奇数,则对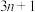 不断地除以2,直到得出一个奇数,记这个奇数为
不断地除以2,直到得出一个奇数,记这个奇数为 .若
.若 ,则称正整数n为“理想数”.
,则称正整数n为“理想数”.
(1)求20以内的质数“理想数”;
(2)已知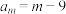 .求m的值;
.求m的值;
(3)将所有“理想数”从小至大依次排列,逐一取倒数后得到数列 ,记
,记 的前n项和为
的前n项和为 ,证明:
,证明: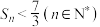 .
.
 ;若n为奇数,则对
;若n为奇数,则对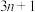 不断地除以2,直到得出一个奇数,记这个奇数为
不断地除以2,直到得出一个奇数,记这个奇数为 .若
.若 ,则称正整数n为“理想数”.
,则称正整数n为“理想数”.(1)求20以内的质数“理想数”;
(2)已知
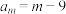 .求m的值;
.求m的值;(3)将所有“理想数”从小至大依次排列,逐一取倒数后得到数列
 ,记
,记 的前n项和为
的前n项和为 ,证明:
,证明: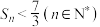 .
.
您最近一年使用:0次
2024-08-10更新
|
931次组卷
|
6卷引用:甘肃省白银市第八中学2024-2025学年高二上学期第1次阶段性考试(10月)数学试题
名校
2 . 已知: ,
, ,
,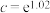 ,那么
,那么 三者的关系是( )
三者的关系是( )
 ,
, ,
,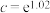 ,那么
,那么 三者的关系是( )
三者的关系是( )A.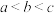 | B. | C.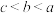 | D.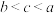 |
您最近一年使用:0次
2024-08-05更新
|
580次组卷
|
3卷引用:甘肃省白银市第八中学2025届高三上学期第一次月考数学试题
名校
解题方法
3 . 已知离心率为 的椭圆
的椭圆 的右焦点为
的右焦点为 ,点
,点 为椭圆上第一象限内的一点,满足
为椭圆上第一象限内的一点,满足 垂直于
垂直于 轴,且
轴,且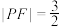 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 的斜率存在,交椭圆
的斜率存在,交椭圆 于
于 两点,
两点, 三点不共线,且直线
三点不共线,且直线 和直线
和直线 关于直线
关于直线 对称,证明:直线
对称,证明:直线 过定点.
过定点.
 的椭圆
的椭圆 的右焦点为
的右焦点为 ,点
,点 为椭圆上第一象限内的一点,满足
为椭圆上第一象限内的一点,满足 垂直于
垂直于 轴,且
轴,且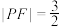 .
.(1)求椭圆
 的方程;
的方程;(2)直线
 的斜率存在,交椭圆
的斜率存在,交椭圆 于
于 两点,
两点, 三点不共线,且直线
三点不共线,且直线 和直线
和直线 关于直线
关于直线 对称,证明:直线
对称,证明:直线 过定点.
过定点.
您最近一年使用:0次
名校
4 . 已知函数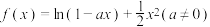 .
.
(1)证明:当 时,
时, 只有1个零点;
只有1个零点;
(2)当 时,讨论
时,讨论 的单调性;
的单调性;
(3)若 ,设
,设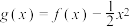 ,证明:
,证明: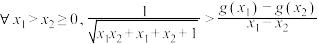 .
.
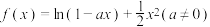 .
.(1)证明:当
 时,
时, 只有1个零点;
只有1个零点;(2)当
 时,讨论
时,讨论 的单调性;
的单调性;(3)若
 ,设
,设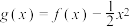 ,证明:
,证明: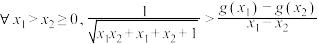 .
.
您最近一年使用:0次
7日内更新
|
238次组卷
|
3卷引用:甘肃省张掖市部分学校2025届高三上学期10月质量检测数学试卷
5 . 如图,我们把由平面内夹角成 的两条数轴Ox,Oy构成的坐标系,称为“完美坐标系”.设
的两条数轴Ox,Oy构成的坐标系,称为“完美坐标系”.设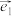 ,
,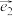 分别为Ox,Oy正方向上的单位向量,若向量
分别为Ox,Oy正方向上的单位向量,若向量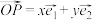 ,则把实数对
,则把实数对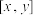 叫做向量
叫做向量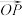 的“完美坐标”.
的“完美坐标”.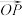 的“完美坐标”为
的“完美坐标”为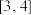 ,求
,求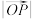 ;
;
(2)已知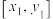 ,
,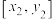 分别为向量
分别为向量 ,
, 的“完美坐标”,证明:
的“完美坐标”,证明: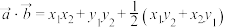 ;
;
(3)若向量 ,
, 的“完美坐标”分别为
的“完美坐标”分别为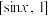 ,
,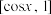 ,设函数
,设函数 ,
,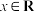 ,求
,求 的值域.
的值域.
 的两条数轴Ox,Oy构成的坐标系,称为“完美坐标系”.设
的两条数轴Ox,Oy构成的坐标系,称为“完美坐标系”.设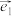 ,
,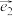 分别为Ox,Oy正方向上的单位向量,若向量
分别为Ox,Oy正方向上的单位向量,若向量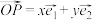 ,则把实数对
,则把实数对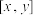 叫做向量
叫做向量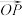 的“完美坐标”.
的“完美坐标”.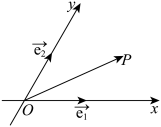
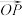 的“完美坐标”为
的“完美坐标”为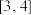 ,求
,求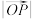 ;
;(2)已知
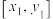 ,
,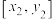 分别为向量
分别为向量 ,
, 的“完美坐标”,证明:
的“完美坐标”,证明: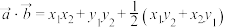 ;
;(3)若向量
 ,
, 的“完美坐标”分别为
的“完美坐标”分别为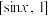 ,
,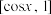 ,设函数
,设函数 ,
,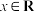 ,求
,求 的值域.
的值域.
您最近一年使用:0次
7日内更新
|
164次组卷
|
2卷引用:甘肃省张掖市部分学校2025届高三上学期10月质量检测数学试卷
名校
解题方法
6 . 若实数 满足
满足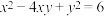 ,则( )
,则( )
 满足
满足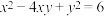 ,则( )
,则( )A.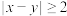 | B.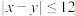 |
C.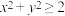 | D.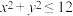 |
您最近一年使用:0次
7日内更新
|
122次组卷
|
3卷引用:甘肃省张掖市部分学校2025届高三上学期10月质量检测数学试卷
名校
解题方法
7 . 已知函数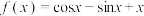 ,则( )
,则( )
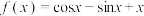 ,则( )
,则( )A. 的图象关于点 的图象关于点 对称 对称 |
B.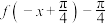 为奇函数 为奇函数 |
C. 是 是 的极小值点 的极小值点 |
D. 在 在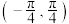 上有极值 上有极值 |
您最近一年使用:0次
7日内更新
|
259次组卷
|
3卷引用:甘肃省张掖市部分学校2025届高三上学期10月质量检测数学试卷
8 . 设A是由若干个正整数组成的集合,且存在3个不同的元素a,b,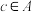 ,使得
,使得 ,则称A为“等差集”.
,则称A为“等差集”.
(1)若集合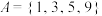 ,
,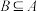 ,且B是“等差集”,用列举法表示所有满足条件的B;
,且B是“等差集”,用列举法表示所有满足条件的B;
(2)若集合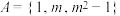 是“等差集”,求m的值;
是“等差集”,求m的值;
(3)已知正整数 ,证明:
,证明: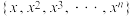 不是“等差集”.
不是“等差集”.
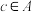 ,使得
,使得 ,则称A为“等差集”.
,则称A为“等差集”.(1)若集合
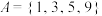 ,
,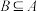 ,且B是“等差集”,用列举法表示所有满足条件的B;
,且B是“等差集”,用列举法表示所有满足条件的B;(2)若集合
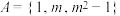 是“等差集”,求m的值;
是“等差集”,求m的值;(3)已知正整数
 ,证明:
,证明: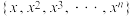 不是“等差集”.
不是“等差集”.
您最近一年使用:0次
2024-10-22更新
|
426次组卷
|
13卷引用:甘肃省陇南市礼县第二中学2024-2025学年高二上学期第一次阶段性检测数学试卷
甘肃省陇南市礼县第二中学2024-2025学年高二上学期第一次阶段性检测数学试卷江西省多校2024-2025学年高一上学期10月月考数学试题湖南省郴州市部分学校2024-2025学年高二上学期第一次月考数学试题河南省名校联考2024-2025学年高一上学期第一次月考数学试题湖南省多校联考2024-2025学年高二上学期10月月考数学试题陕西省西安市黄河中学2024-2025学年高一上学期第一次月考数学试题内蒙古名校联盟2024-2025学年高一上学期10月大联考数学试题辽宁省凌源市2024-2025学年高一上学期第一次月考(10月)数学卷辽宁省朝阳市建平县实验中学2024-2025学年高一上学期10月月考数学试题安徽省名校联盟2024-2025学年高一上学期10月大联考数学试卷陕西省咸阳市乾县杨汉中学2024-2025学年高二上学期第一次阶段性测试数学试卷广西钦州市第四中学2025届高三上学期8月考试数学试题河北省保定市安国中学2024-2025学年高一上学期第一次月考数学试题
解题方法
9 . 对于一组向量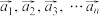 (
(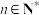 且
且 ),令
),令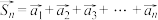 ,如果存在
,如果存在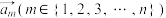 ,使得
,使得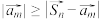 ,那么称
,那么称 ,是该向量组的“
,是该向量组的“ 向量”.
向量”.
(1)设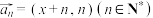 ,若
,若 是向量组
是向量组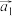 ,
, ,
, 的“
的“ 向量”,求实数
向量”,求实数 的取值范围;
的取值范围;
(2)若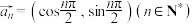 ,向量组
,向量组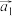 ,
, ,
, ,
, ,
, 是否存在“
是否存在“ 向量”?若存在求出所有的“
向量”?若存在求出所有的“ 向量”,若不存在说明理由;
向量”,若不存在说明理由;
(3)已知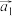 ,
, ,
, 均是向量组
均是向量组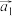 ,
, ,
, 的“
的“ 向量”,其中
向量”,其中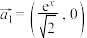 ,
,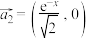 ,求证:
,求证: 可以写成一个关于
可以写成一个关于 的二次多项式与一个关于
的二次多项式与一个关于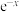 的二次多项式的乘积.
的二次多项式的乘积.
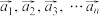 (
(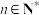 且
且 ),令
),令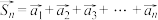 ,如果存在
,如果存在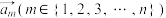 ,使得
,使得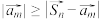 ,那么称
,那么称 ,是该向量组的“
,是该向量组的“ 向量”.
向量”.(1)设
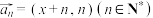 ,若
,若 是向量组
是向量组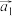 ,
, ,
, 的“
的“ 向量”,求实数
向量”,求实数 的取值范围;
的取值范围;(2)若
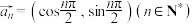 ,向量组
,向量组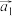 ,
, ,
, ,
, ,
, 是否存在“
是否存在“ 向量”?若存在求出所有的“
向量”?若存在求出所有的“ 向量”,若不存在说明理由;
向量”,若不存在说明理由;(3)已知
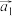 ,
, ,
, 均是向量组
均是向量组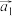 ,
, ,
, 的“
的“ 向量”,其中
向量”,其中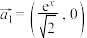 ,
,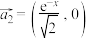 ,求证:
,求证: 可以写成一个关于
可以写成一个关于 的二次多项式与一个关于
的二次多项式与一个关于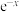 的二次多项式的乘积.
的二次多项式的乘积.
您最近一年使用:0次
2024-10-21更新
|
141次组卷
|
3卷引用:甘肃省陇南市礼县第二中学2024-2025学年高二上学期第一次阶段性检测数学试卷
10 . 已知数列 满足
满足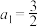 ,对任意
,对任意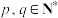 ,都有
,都有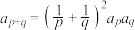 ,设
,设 ,则对任意
,则对任意 ,下列结论恒成立的是( )
,下列结论恒成立的是( )
 满足
满足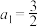 ,对任意
,对任意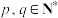 ,都有
,都有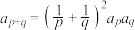 ,设
,设 ,则对任意
,则对任意 ,下列结论恒成立的是( )
,下列结论恒成立的是( )A. | B. |
C. | D.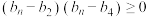 |
您最近一年使用:0次



