名校
解题方法
1 . 已知点 是圆
是圆 的动点,过
的动点,过 作
作 轴,
轴, 为垂足,且
为垂足,且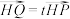 ,
, ,记动点
,记动点 ,
, 的轨迹分别为
的轨迹分别为 ,
, .
.
(1)证明: ,
, 有相同的离心率;
有相同的离心率;
(2)若直线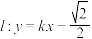 与曲线
与曲线 交于
交于 ,
, ,与曲线
,与曲线 交于
交于 ,
, ,与圆
,与圆 交于
交于 ,
, ,当
,当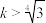 时,试比较
时,试比较 与
与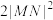 的大小.
的大小.
 是圆
是圆 的动点,过
的动点,过 作
作 轴,
轴, 为垂足,且
为垂足,且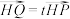 ,
, ,记动点
,记动点 ,
, 的轨迹分别为
的轨迹分别为 ,
, .
.(1)证明:
 ,
, 有相同的离心率;
有相同的离心率;(2)若直线
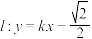 与曲线
与曲线 交于
交于 ,
, ,与曲线
,与曲线 交于
交于 ,
, ,与圆
,与圆 交于
交于 ,
, ,当
,当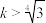 时,试比较
时,试比较 与
与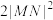 的大小.
的大小.
您最近一年使用:0次
2024-02-28更新
|
440次组卷
|
2卷引用:浙江省金华市2023-2024学年高三上学期2月期末考试数学试题
名校
解题方法
2 . 已知抛物线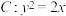 的焦点为
的焦点为 ,准线为
,准线为 ,点
,点 ,
, 在
在 上(
上( 在第一象限),点
在第一象限),点 在
在 上,
上, ,
,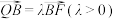 ,( )
,( )
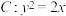 的焦点为
的焦点为 ,准线为
,准线为 ,点
,点 ,
, 在
在 上(
上( 在第一象限),点
在第一象限),点 在
在 上,
上, ,
,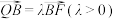 ,( )
,( )A.若 ,则 ,则 | B.若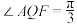 ,则 ,则 |
C.则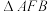 的面积最小值为 的面积最小值为 | D.则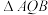 的面积大于 的面积大于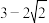 |
您最近一年使用:0次
2024-02-28更新
|
1536次组卷
|
5卷引用:浙江省金华市2023-2024学年高三上学期2月期末考试数学试题
浙江省金华市2023-2024学年高三上学期2月期末考试数学试题(已下线)第六套 九省联考全真模拟湖南省2024届高三数学新改革提高训练五(九省联考题型)(已下线)压轴小题2 平面几何中的双动点问题(4月)(已下线)压轴小题7 抛物线性质的综合问题
解题方法
3 . 已知 ,
, 分别是双曲线
分别是双曲线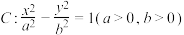 的左,右顶点,
的左,右顶点,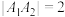 ,点
,点 到其中一条渐近线的距离为
到其中一条渐近线的距离为 .
.
(1)求双曲线C的方程:
(2)过点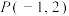 的直线l与C交于M,N两点(异于
的直线l与C交于M,N两点(异于 ,
, 两点),直线OP与直线
两点),直线OP与直线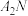 交于点Q.若直线
交于点Q.若直线 与
与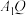 的斜率分别为
的斜率分别为 ,
, ,试问
,试问 是否为定值?若是,求出此定值;否不是,请说明理由.
是否为定值?若是,求出此定值;否不是,请说明理由.
 ,
, 分别是双曲线
分别是双曲线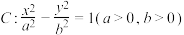 的左,右顶点,
的左,右顶点,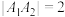 ,点
,点 到其中一条渐近线的距离为
到其中一条渐近线的距离为 .
.(1)求双曲线C的方程:
(2)过点
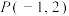 的直线l与C交于M,N两点(异于
的直线l与C交于M,N两点(异于 ,
, 两点),直线OP与直线
两点),直线OP与直线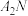 交于点Q.若直线
交于点Q.若直线 与
与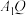 的斜率分别为
的斜率分别为 ,
, ,试问
,试问 是否为定值?若是,求出此定值;否不是,请说明理由.
是否为定值?若是,求出此定值;否不是,请说明理由.
您最近一年使用:0次
解题方法
4 . 已知函数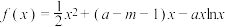 .
.
(1)若 时,
时, 在其定义域内不是单调函数,求a的取值范围;
在其定义域内不是单调函数,求a的取值范围;
(2)若 ,
, 时,函数
时,函数 有两个极值点
有两个极值点 ,
,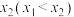 ,求证:
,求证: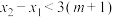 .
.
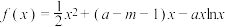 .
.(1)若
 时,
时, 在其定义域内不是单调函数,求a的取值范围;
在其定义域内不是单调函数,求a的取值范围;(2)若
 ,
, 时,函数
时,函数 有两个极值点
有两个极值点 ,
,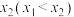 ,求证:
,求证: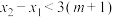 .
.
您最近一年使用:0次
名校
5 . 已知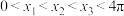 ,函数
,函数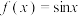 在点
在点 处的切线均经过坐标原点,则( )
处的切线均经过坐标原点,则( )
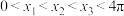 ,函数
,函数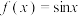 在点
在点 处的切线均经过坐标原点,则( )
处的切线均经过坐标原点,则( )A.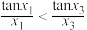 | B.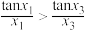 | C.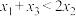 | D.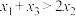 |
您最近一年使用:0次
2024-02-04更新
|
3283次组卷
|
9卷引用:浙江省温州市2024届高三上学期期末考试数学试题
解题方法
6 . 已知双曲线 的左右顶点分别为
的左右顶点分别为 ,点
,点 满足
满足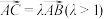 ,点
,点 为双曲线右支上任意一点(异于点
为双曲线右支上任意一点(异于点 ),以
),以 为直径的圆交直线
为直径的圆交直线 于点
于点 ,直线
,直线 与直线
与直线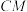 交于点
交于点 .若
.若 点的横坐标等于该圆的半径,则该双曲线的离心率是
点的横坐标等于该圆的半径,则该双曲线的离心率是__________ .
 的左右顶点分别为
的左右顶点分别为 ,点
,点 满足
满足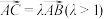 ,点
,点 为双曲线右支上任意一点(异于点
为双曲线右支上任意一点(异于点 ),以
),以 为直径的圆交直线
为直径的圆交直线 于点
于点 ,直线
,直线 与直线
与直线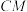 交于点
交于点 .若
.若 点的横坐标等于该圆的半径,则该双曲线的离心率是
点的横坐标等于该圆的半径,则该双曲线的离心率是
您最近一年使用:0次
名校
7 . 已知 ,
,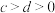 ,
,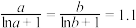 ,
, ,则( )
,则( )
 ,
,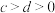 ,
,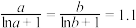 ,
, ,则( )
,则( )A.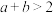 | B. | C.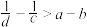 | D. |
您最近一年使用:0次
2024-01-29更新
|
1056次组卷
|
3卷引用:浙江省宁波市宁波九校2023-2024学年高三上学期1月期末数学试题
名校
8 . 在几何学常常需要考虑曲线的弯曲程度,为此我们需要刻画曲线的弯曲程度.考察如图所示的光滑曲线C: 上的曲线段
上的曲线段 ,其弧长为
,其弧长为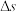 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线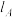 也随着转动到B点的切线
也随着转动到B点的切线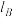 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为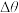 (它等于
(它等于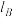 的倾斜角与
的倾斜角与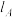 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义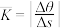 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即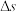 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义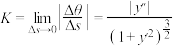 (若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示
(若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示 在点A处的一阶、二阶导数)
在点A处的一阶、二阶导数)
(2)求椭圆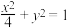 在
在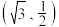 处的曲率;
处的曲率;
(3)定义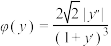 为曲线
为曲线 的“柯西曲率”.已知在曲线
的“柯西曲率”.已知在曲线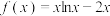 上存在两点
上存在两点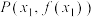 和
和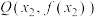 ,且P,Q处的“柯西曲率”相同,求
,且P,Q处的“柯西曲率”相同,求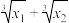 的取值范围.
的取值范围.
 上的曲线段
上的曲线段 ,其弧长为
,其弧长为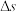 ,当动点从A沿曲线段
,当动点从A沿曲线段 运动到B点时,A点的切线
运动到B点时,A点的切线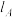 也随着转动到B点的切线
也随着转动到B点的切线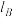 ,记这两条切线之间的夹角为
,记这两条切线之间的夹角为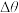 (它等于
(它等于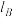 的倾斜角与
的倾斜角与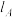 的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义
的倾斜角之差).显然,当弧长固定时,夹角越大,曲线的弯曲程度就越大;当夹角固定时,弧长越小则弯曲程度越大,因此可以定义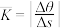 为曲线段
为曲线段 的平均曲率;显然当B越接近A,即
的平均曲率;显然当B越接近A,即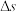 越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义
越小,K就越能精确刻画曲线C在点A处的弯曲程度,因此定义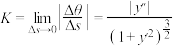 (若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示
(若极限存在)为曲线C在点A处的曲率.(其中y',y''分别表示 在点A处的一阶、二阶导数)
在点A处的一阶、二阶导数)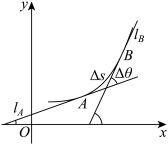
(2)求椭圆
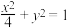 在
在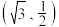 处的曲率;
处的曲率;(3)定义
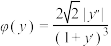 为曲线
为曲线 的“柯西曲率”.已知在曲线
的“柯西曲率”.已知在曲线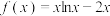 上存在两点
上存在两点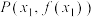 和
和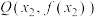 ,且P,Q处的“柯西曲率”相同,求
,且P,Q处的“柯西曲率”相同,求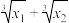 的取值范围.
的取值范围.
您最近一年使用:0次
2024-01-29更新
|
3806次组卷
|
12卷引用:浙江省宁波市镇海中学2024届高三上学期期末数学试题
浙江省宁波市镇海中学2024届高三上学期期末数学试题湖北省武汉市武钢三中2024届高三下学期开学考试数学试题(已下线)第四套 九省联考全真模拟(已下线)压轴题函数与导数新定义题(九省联考第19题模式)练(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)微考点2-5 新高考新试卷结构19题压轴题新定义导数试题分类汇编(已下线)拔高点突破05 函数与导数背景下的新定义压轴解答题(九大题型)(已下线)专题7 导数与极值点偏移【讲】(已下线)专题5 解析几何中的新定义压轴大题(三)【讲】湖南省长沙外国语学校2023-2024学年高二下学期3月月考数学试题山东省菏泽市定陶区第一中学2023-2024学年高二下学期第一次月考数学试题江西省萍乡市2024-2025学年高二上学期期中考试数学试卷
名校
9 . 设数阵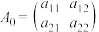 ,其中
,其中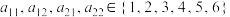 .设
.设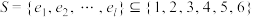 ,其中
,其中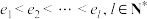 且
且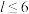 .定义变换
.定义变换 为“对于数阵的每一行,若其中有
为“对于数阵的每一行,若其中有 或
或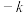 ,则将这一行中每个数都乘以
,则将这一行中每个数都乘以 ;若其中没有
;若其中没有 且没有
且没有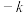 ,则这一行中所有数均保持不变”
,则这一行中所有数均保持不变”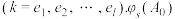 表示“将
表示“将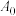 经过
经过 变换得到
变换得到 ,再将
,再将 经过
经过 变换得到
变换得到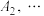 以此类推,最后将
以此类推,最后将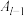 经过
经过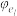 变换得到
变换得到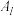 .记数阵
.记数阵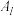 中四个数的和为
中四个数的和为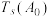 .
.
(1)若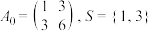 ,写出
,写出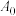 经过
经过 变换后得到的数阵
变换后得到的数阵 ,并求
,并求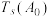 的值;
的值;
(2)若 ,求
,求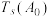 的所有可能取值的和;
的所有可能取值的和;
(3)对任意确定的一个数阵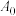 ,证明:
,证明: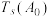 的所有可能取值的和不超过
的所有可能取值的和不超过 .
.
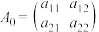 ,其中
,其中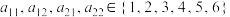 .设
.设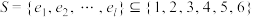 ,其中
,其中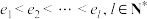 且
且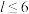 .定义变换
.定义变换 为“对于数阵的每一行,若其中有
为“对于数阵的每一行,若其中有 或
或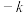 ,则将这一行中每个数都乘以
,则将这一行中每个数都乘以 ;若其中没有
;若其中没有 且没有
且没有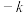 ,则这一行中所有数均保持不变”
,则这一行中所有数均保持不变”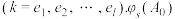 表示“将
表示“将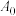 经过
经过 变换得到
变换得到 ,再将
,再将 经过
经过 变换得到
变换得到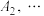 以此类推,最后将
以此类推,最后将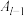 经过
经过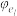 变换得到
变换得到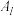 .记数阵
.记数阵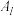 中四个数的和为
中四个数的和为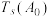 .
.(1)若
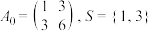 ,写出
,写出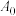 经过
经过 变换后得到的数阵
变换后得到的数阵 ,并求
,并求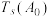 的值;
的值;(2)若
 ,求
,求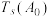 的所有可能取值的和;
的所有可能取值的和;(3)对任意确定的一个数阵
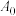 ,证明:
,证明: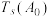 的所有可能取值的和不超过
的所有可能取值的和不超过 .
.
您最近一年使用:0次
2023-12-20更新
|
2253次组卷
|
7卷引用:浙江省温州市第五十一中学2024届高三上学期期末数学试题
浙江省温州市第五十一中学2024届高三上学期期末数学试题北京市海淀区中关村中学2024届高三上学期12月月考数学试题(已下线)最新模拟重组精华卷2 -模块一 各地期末考试精选汇编(已下线)专题1 集合新定义题(九省联考第19题模式)练(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(三)【讲】
10 . 已知函数 在定义域内有两个不同的零点
在定义域内有两个不同的零点 ,.
,.
(1)求证: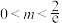
(2)已知 ,若存在
,若存在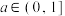 ,不等式
,不等式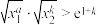 对任意的
对任意的 总成立,求
总成立,求 的取值范围.
的取值范围.
 在定义域内有两个不同的零点
在定义域内有两个不同的零点 ,.
,.(1)求证:
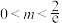
(2)已知
 ,若存在
,若存在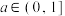 ,不等式
,不等式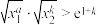 对任意的
对任意的 总成立,求
总成立,求 的取值范围.
的取值范围.
您最近一年使用:0次



