名校
1 . 在计算机科学中, 维数组
维数组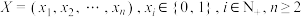 是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于
是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于 维数组
维数组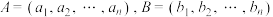 ,定义
,定义 与
与 的差为
的差为 与
与 之间的距离为
之间的距离为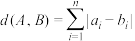 .
.
(1)若 维数组
维数组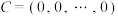 ,证明:
,证明: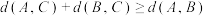 ;
;
(2)证明:对任意的数组 ,有
,有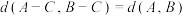 ;
;
(3)设集合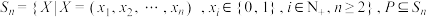 ,若集合
,若集合 中有
中有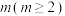 个
个 维数组,记
维数组,记 中所有两元素间的距离的平均值为
中所有两元素间的距离的平均值为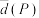 ,证明:
,证明: .
.
 维数组
维数组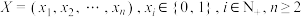 是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于
是一种基础而重要的数据结构,它在各种编程语言中被广泛使用.对于 维数组
维数组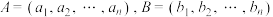 ,定义
,定义 与
与 的差为
的差为 与
与 之间的距离为
之间的距离为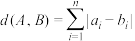 .
.(1)若
 维数组
维数组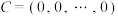 ,证明:
,证明: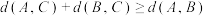 ;
;(2)证明:对任意的数组
 ,有
,有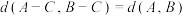 ;
;(3)设集合
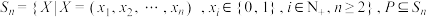 ,若集合
,若集合 中有
中有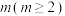 个
个 维数组,记
维数组,记 中所有两元素间的距离的平均值为
中所有两元素间的距离的平均值为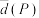 ,证明:
,证明: .
.
您最近半年使用:0次
2 . 如图, 是边长为2的正方形纸片,沿某动直线
是边长为2的正方形纸片,沿某动直线 为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点
为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点 都落在边
都落在边 上,记为
上,记为 ;折痕
;折痕 与
与 交于点
交于点 ,点
,点 满足关系式
满足关系式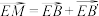 .以点
.以点 为坐标原点建立坐标系,若曲线
为坐标原点建立坐标系,若曲线 是由点
是由点 的轨迹及其关于边
的轨迹及其关于边 对称的曲线组成的,等腰梯形
对称的曲线组成的,等腰梯形 的
的 分别与曲线
分别与曲线 切于点P、Q、
切于点P、Q、 ,且
,且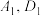 在x轴上.则梯形
在x轴上.则梯形 的面积最小值为( )
的面积最小值为( )
 是边长为2的正方形纸片,沿某动直线
是边长为2的正方形纸片,沿某动直线 为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点
为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点 都落在边
都落在边 上,记为
上,记为 ;折痕
;折痕 与
与 交于点
交于点 ,点
,点 满足关系式
满足关系式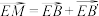 .以点
.以点 为坐标原点建立坐标系,若曲线
为坐标原点建立坐标系,若曲线 是由点
是由点 的轨迹及其关于边
的轨迹及其关于边 对称的曲线组成的,等腰梯形
对称的曲线组成的,等腰梯形 的
的 分别与曲线
分别与曲线 切于点P、Q、
切于点P、Q、 ,且
,且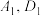 在x轴上.则梯形
在x轴上.则梯形 的面积最小值为( )
的面积最小值为( )
| A.6 | B. | C.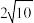 | D. |
您最近半年使用:0次
3 . 对于数列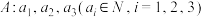 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列 变换成数列
变换成数列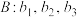 ,其中
,其中 ,且
,且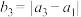 .这种“
.这种“ 变换”记作
变换”记作 ,继续对数列
,继续对数列 进行“
进行“ 变换”,得到数列
变换”,得到数列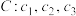 ,依此类推,当得到的数列各项均为0时变换结束.
,依此类推,当得到的数列各项均为0时变换结束.
(1)写出数列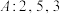 ,经过6次“
,经过6次“ 变换”后得到的数列;
变换”后得到的数列;
(2)若 不全相等,判断数列
不全相等,判断数列 经过不断的“
经过不断的“ 变换”是否会结束,并说明理由;
变换”是否会结束,并说明理由;
(3)设数列 经过
经过 次“
次“ 变换”得到的数列各项之和最小,求
变换”得到的数列各项之和最小,求 的最小值.
的最小值.
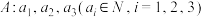 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列 变换成数列
变换成数列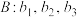 ,其中
,其中 ,且
,且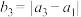 .这种“
.这种“ 变换”记作
变换”记作 ,继续对数列
,继续对数列 进行“
进行“ 变换”,得到数列
变换”,得到数列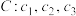 ,依此类推,当得到的数列各项均为0时变换结束.
,依此类推,当得到的数列各项均为0时变换结束.(1)写出数列
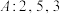 ,经过6次“
,经过6次“ 变换”后得到的数列;
变换”后得到的数列;(2)若
 不全相等,判断数列
不全相等,判断数列 经过不断的“
经过不断的“ 变换”是否会结束,并说明理由;
变换”是否会结束,并说明理由;(3)设数列
 经过
经过 次“
次“ 变换”得到的数列各项之和最小,求
变换”得到的数列各项之和最小,求 的最小值.
的最小值.
您最近半年使用:0次
解题方法
4 . 对于数列 ,若存在
,若存在 ,使得对任意
,使得对任意 ,总有
,总有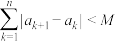 ,则称
,则称 为“有界变差数列”.
为“有界变差数列”.
(1)若各项均为正数的等比数列 为有界变差数列,求其公比q的取值范围;
为有界变差数列,求其公比q的取值范围;
(2)若数列 满足
满足 ,且
,且 ,证明:
,证明: 是有界变差数列;
是有界变差数列;
(3)若 ,
,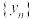 均为有界变差数列,且
均为有界变差数列,且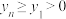 ,证明:
,证明: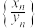 是有界变差数列.
是有界变差数列.
 ,若存在
,若存在 ,使得对任意
,使得对任意 ,总有
,总有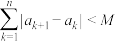 ,则称
,则称 为“有界变差数列”.
为“有界变差数列”.(1)若各项均为正数的等比数列
 为有界变差数列,求其公比q的取值范围;
为有界变差数列,求其公比q的取值范围;(2)若数列
 满足
满足 ,且
,且 ,证明:
,证明: 是有界变差数列;
是有界变差数列;(3)若
 ,
,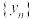 均为有界变差数列,且
均为有界变差数列,且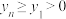 ,证明:
,证明: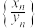 是有界变差数列.
是有界变差数列.
您最近半年使用:0次
5 . 已知各项均不为0的数列 满足
满足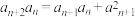 (
( 是正整数),
是正整数),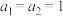 ,定义函数
,定义函数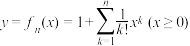 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求证:数列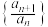 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)记函数 ,其中
,其中 .
.
(i)证明:对任意 ,
, ;
;
(ii)数列 满足
满足 ,设
,设 为数列
为数列 的前
的前 项和.数列
项和.数列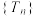 的极限的严格定义为:若存在一个常数
的极限的严格定义为:若存在一个常数 ,使得对任意给定的正实数
,使得对任意给定的正实数 (不论它多么小),总存在正整数m满足:当
(不论它多么小),总存在正整数m满足:当 时,恒有
时,恒有 成立,则称
成立,则称 为数列
为数列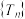 的极限.试根据以上定义求出数列
的极限.试根据以上定义求出数列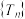 的极限
的极限 .
.
 满足
满足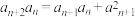 (
( 是正整数),
是正整数),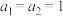 ,定义函数
,定义函数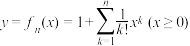 ,
, 是自然对数的底数.
是自然对数的底数.(1)求证:数列
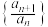 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;(2)记函数
 ,其中
,其中 .
.(i)证明:对任意
 ,
, ;
;(ii)数列
 满足
满足 ,设
,设 为数列
为数列 的前
的前 项和.数列
项和.数列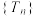 的极限的严格定义为:若存在一个常数
的极限的严格定义为:若存在一个常数 ,使得对任意给定的正实数
,使得对任意给定的正实数 (不论它多么小),总存在正整数m满足:当
(不论它多么小),总存在正整数m满足:当 时,恒有
时,恒有 成立,则称
成立,则称 为数列
为数列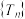 的极限.试根据以上定义求出数列
的极限.试根据以上定义求出数列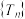 的极限
的极限 .
.
您最近半年使用:0次
6 . 已知椭圆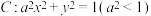 的长轴为4,直线
的长轴为4,直线 与圆
与圆 相切于点
相切于点 ,与
,与 相交于
相交于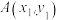 ,
,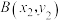 两点,且
两点,且 ,
, ,
,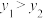 .
.
(1)记 的离心率为
的离心率为 ,证明:
,证明: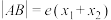 ;
;
(2)若 轴右侧的点
轴右侧的点 在
在 上,且
上,且 轴,
轴,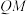 ,
,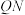 是圆
是圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, (
( 在
在 上方),求
上方),求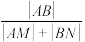 的值.
的值.
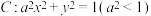 的长轴为4,直线
的长轴为4,直线 与圆
与圆 相切于点
相切于点 ,与
,与 相交于
相交于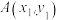 ,
,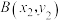 两点,且
两点,且 ,
, ,
,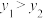 .
.(1)记
 的离心率为
的离心率为 ,证明:
,证明: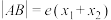 ;
;(2)若
 轴右侧的点
轴右侧的点 在
在 上,且
上,且 轴,
轴,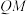 ,
,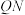 是圆
是圆 的两条切线,切点分别为
的两条切线,切点分别为 ,
, (
( 在
在 上方),求
上方),求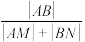 的值.
的值.
您最近半年使用:0次
7 . 设 是各项为正的无穷数列,若对于
是各项为正的无穷数列,若对于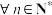 ,
,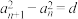 (d:为非零常数),则称数列
(d:为非零常数),则称数列 为等方差数列.那么( )
为等方差数列.那么( )
 是各项为正的无穷数列,若对于
是各项为正的无穷数列,若对于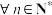 ,
,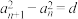 (d:为非零常数),则称数列
(d:为非零常数),则称数列 为等方差数列.那么( )
为等方差数列.那么( )A.若 是等方差数列,则 是等方差数列,则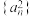 是等差数列 是等差数列 |
B.数列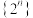 为等方差数列 为等方差数列 |
C.若 是等方差数列,则数列 是等方差数列,则数列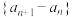 中存在小于1的项 中存在小于1的项 |
D.若 是等方差数列,则存在正整数n,使得 是等方差数列,则存在正整数n,使得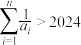 |
您最近半年使用:0次
8 . 设函数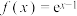 ,
, .
.
(1)求函数 的单调区间;
的单调区间;
(2)若总存在两条直线和曲线 与
与 都相切,求
都相切,求 的取值范围.
的取值范围.
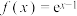 ,
, .
.(1)求函数
 的单调区间;
的单调区间;(2)若总存在两条直线和曲线
 与
与 都相切,求
都相切,求 的取值范围.
的取值范围.
您最近半年使用:0次
9 . 已知抛物线C: (
( )的准线与圆O:
)的准线与圆O: 相切.
相切.
(1)求C的方程;
(2)设点P是C上的一点,点A,B是C的准线上两个不同的点,且圆O是 的内切圆.
的内切圆.
①若 ,求点P的横坐标;
,求点P的横坐标;
②求 面积的最小值.
面积的最小值.
 (
( )的准线与圆O:
)的准线与圆O: 相切.
相切.(1)求C的方程;
(2)设点P是C上的一点,点A,B是C的准线上两个不同的点,且圆O是
 的内切圆.
的内切圆.①若
 ,求点P的横坐标;
,求点P的横坐标;②求
 面积的最小值.
面积的最小值.
您最近半年使用:0次
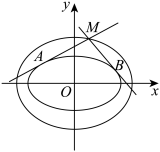
10 . 已知曲线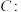
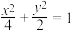 ,
, 是坐标原点, 过点
是坐标原点, 过点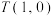 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点.
两点.
(1)当 与
与 轴垂直时,求
轴垂直时,求 的面积;
的面积;
(2)过圆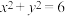 上任意一点
上任意一点 作直线
作直线 ,
, ,分别与曲线
,分别与曲线 切于
切于 ,
, 两 点,求证:
两 点,求证: ;
; 的直线
的直线 与双曲线
与双曲线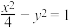 交于
交于 ,
, 两点(
两点( ,
, 不与
不与 轴重合).记直线
轴重合).记直线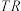 的斜率为
的斜率为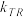 ,直线
,直线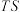 斜率为
斜率为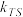 , 当
, 当 时,求证:
时,求证: 与
与 都是定值.
都是定值.
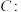
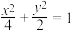 ,
, 是坐标原点, 过点
是坐标原点, 过点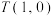 的直线
的直线 与曲线
与曲线 交于
交于 ,
, 两点.
两点.(1)当
 与
与 轴垂直时,求
轴垂直时,求 的面积;
的面积;(2)过圆
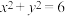 上任意一点
上任意一点 作直线
作直线 ,
, ,分别与曲线
,分别与曲线 切于
切于 ,
, 两 点,求证:
两 点,求证: ;
;
 的直线
的直线 与双曲线
与双曲线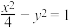 交于
交于 ,
, 两点(
两点( ,
, 不与
不与 轴重合).记直线
轴重合).记直线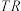 的斜率为
的斜率为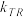 ,直线
,直线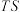 斜率为
斜率为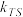 , 当
, 当 时,求证:
时,求证: 与
与 都是定值.
都是定值.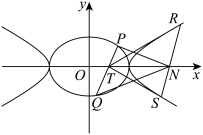
您最近半年使用:0次



