名校
1 . 已知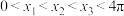 ,函数
,函数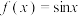 在点
在点 处的切线均经过坐标原点,则( )
处的切线均经过坐标原点,则( )
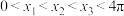 ,函数
,函数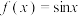 在点
在点 处的切线均经过坐标原点,则( )
处的切线均经过坐标原点,则( )A.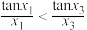 | B.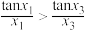 | C.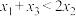 | D.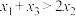 |
您最近一年使用:0次
2024-02-04更新
|
3201次组卷
|
8卷引用:黄金卷02(2024新题型)
(已下线)黄金卷02(2024新题型)浙江省温州市2024届高三上学期期末考试数学试题湖南省2024届高三数学新改革提高训练五(九省联考题型)安徽省阜阳市阜阳一中2023-2024学年高二下学期开学检测数学试题(已下线)新题型01 新高考新结构二十一大考点汇总-3上海市浦东新区上海实验学校2024届高三下学期开学考试数学试题甘肃省兰州市西北师范大学附属中学2024届高三第三次诊断考试数学试题辽宁省IC联盟高二下学期6月阶段性质量检测数学试题
名校
2 . 设 为实数,若实数
为实数,若实数 是关于
是关于 的方程
的方程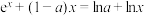 的解,则
的解,则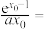
_________ .
 为实数,若实数
为实数,若实数 是关于
是关于 的方程
的方程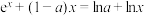 的解,则
的解,则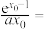
您最近一年使用:0次
名校
解题方法
3 . 已知定义在 上的函数
上的函数 满足:
满足: ,且当
,且当 时,
时,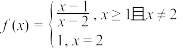 ,下列说法正确的是( )
,下列说法正确的是( )
 上的函数
上的函数 满足:
满足: ,且当
,且当 时,
时,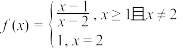 ,下列说法正确的是( )
,下列说法正确的是( )A. 的值域为 的值域为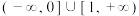 |
B. 在 在 上为减函数 上为减函数 |
C. 在 在 上有唯一的零点 上有唯一的零点 |
D.若方程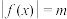 有4个不同的解 有4个不同的解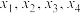 ,且 ,且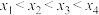 ,则 ,则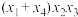 的取值范围是 的取值范围是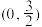 |
您最近一年使用:0次
名校
4 . 已知函数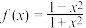 .
.
(1)求证:① ;
;
②函数 的零点个数为奇数;
的零点个数为奇数;
(2)记函数 的值域为A,若至少有两个不同的
的值域为A,若至少有两个不同的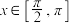 ,使得
,使得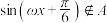 ,求正数
,求正数 的取值范围.
的取值范围.
 .
.(1)求证:①
 ;
;②函数
 的零点个数为奇数;
的零点个数为奇数;(2)记函数
 的值域为A,若至少有两个不同的
的值域为A,若至少有两个不同的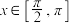 ,使得
,使得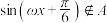 ,求正数
,求正数 的取值范围.
的取值范围.
您最近一年使用:0次
2023-02-22更新
|
539次组卷
|
4卷引用:江苏省泰州市2022-2023学年高一上学期期末数学试题
江苏省泰州市2022-2023学年高一上学期期末数学试题江苏省泰州市靖江高级中学2022-2023学年高一下学期3月月考数学试题江苏省苏南八校2023-2024学年高一上学期12月联考数学试卷(已下线)模块五 专题6 重组综合练(江苏)期末终极研习室(2023-2024学年第一学期)高一人教A版
名校
解题方法
5 . 已知函数 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
 ,则下列说法中正确的是( )
,则下列说法中正确的是( )A.若 为方程 为方程 的两实数根,且 的两实数根,且 ,则 ,则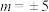 |
B.若方程 的两实数根都在 的两实数根都在 ,则实数 ,则实数 的取值范围是 的取值范围是 |
C.若 , ,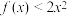 ,则实数 ,则实数 的取值范围是 的取值范围是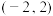 |
D.若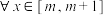 , ,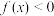 ,则实数 ,则实数 的取值范围是 的取值范围是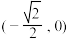 |
您最近一年使用:0次
2022-12-11更新
|
1021次组卷
|
6卷引用:江苏省南京市高淳高级中学2022-2023学年高一上学期10月月考数学试题
名校
6 . 已知函数 ,若
,若 有6个不同的零点分别为
有6个不同的零点分别为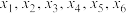 ,且
,且 ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,若
,若 有6个不同的零点分别为
有6个不同的零点分别为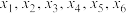 ,且
,且 ,则下列说法正确的是( )
,则下列说法正确的是( )A.当 时, 时, |
B. 的取值范围为 的取值范围为 |
C.当 时, 时, 的取值范围为 的取值范围为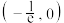 |
D.当 时, 时,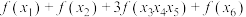 的取值范围为 的取值范围为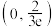 |
您最近一年使用:0次
2022-11-17更新
|
1220次组卷
|
9卷引用:第5章 导数及其应用 单元综合检测(难点)-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)
第5章 导数及其应用 单元综合检测(难点)-2022-2023学年高二数学《基础·重点·难点 》全面题型高分突破(苏教版2019选择性必修第一册)山西省2023届高三上学期11月质量检测数学试题(已下线)2023届高三押题卷二(测试范围:高考全部内容)山西省朔州市怀仁市第一中学校等学校2024届高三上学期摸底数学试题江西省余干县黄金埠中学2022-2023学年高二下学期期中考试数学试题辽宁省沈阳市东北育才学校2023届高三高考适应性测试(二)数学试题吉林省白城市第一中学2023-2024学年高二下学期6月月考数学试题广东省湛江第一中学2023-2024学年高二下学期第二次月考数学试题辽宁省沈阳市辽宁实验中学2025届高三上学期10月月考数学试题
名校
解题方法
7 . 已知函数 ,
, ,若
,若 与
与 图象的公共点个数为
图象的公共点个数为 ,且这些公共点的横坐标从小到大依次为
,且这些公共点的横坐标从小到大依次为 ,
, ,…,
,…, ,则下列说法正确的有( )
,则下列说法正确的有( )
 ,
, ,若
,若 与
与 图象的公共点个数为
图象的公共点个数为 ,且这些公共点的横坐标从小到大依次为
,且这些公共点的横坐标从小到大依次为 ,
, ,…,
,…, ,则下列说法正确的有( )
,则下列说法正确的有( )A.若 ,则 ,则 | B.若 ,则 ,则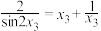 |
C.若 ,则 ,则 | D.若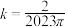 ,则 ,则 |
您最近一年使用:0次
2022-11-05更新
|
713次组卷
|
3卷引用:江苏省扬州中学2022-2023学年高三上学期1月月考数学试题
名校
8 . 定义:若函数 的图像上存在一点
的图像上存在一点 与
与 的图像上一点
的图像上一点 关于
关于 轴对称,则称
轴对称,则称 与
与 具备“
具备“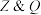 关系”.
关系”.
(1)若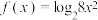 ,
, ,判断
,判断 与
与 是否具备“
是否具备“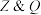 关系”,请说明理由;
关系”,请说明理由;
(2)若 与
与 具备“
具备“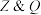 关系”,求实数
关系”,求实数 的范围;
的范围;
(3)若 ,且
,且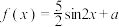 与
与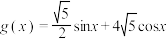 不具备“
不具备“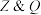 关系”,求整数
关系”,求整数 的最大值.
的最大值.
 的图像上存在一点
的图像上存在一点 与
与 的图像上一点
的图像上一点 关于
关于 轴对称,则称
轴对称,则称 与
与 具备“
具备“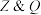 关系”.
关系”.(1)若
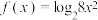 ,
, ,判断
,判断 与
与 是否具备“
是否具备“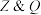 关系”,请说明理由;
关系”,请说明理由;(2)若
 与
与 具备“
具备“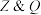 关系”,求实数
关系”,求实数 的范围;
的范围;(3)若
 ,且
,且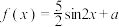 与
与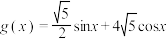 不具备“
不具备“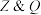 关系”,求整数
关系”,求整数 的最大值.
的最大值.
您最近一年使用:0次
名校
9 . 悬链线(Catenary)指的是一种曲线,指两端固定的一条(粗细与质量分布)均匀,柔软(不能伸长)的链条,在重力的作用下所具有的曲线形状,适当选择坐标系后,悬链线的方程是一个双曲余弦函数,其解析式为 ,与之对应的函数
,与之对应的函数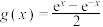 称为双曲正弦函数,令
称为双曲正弦函数,令 .
.
(1)若关于 的方程
的方程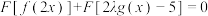 在
在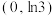 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(2)已知函数 ,若对任意的
,若对任意的 ,总存在不同的
,总存在不同的
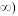 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 ,与之对应的函数
,与之对应的函数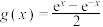 称为双曲正弦函数,令
称为双曲正弦函数,令 .
.(1)若关于
 的方程
的方程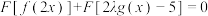 在
在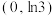 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;(2)已知函数
 ,若对任意的
,若对任意的 ,总存在不同的
,总存在不同的
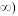 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-02-03更新
|
440次组卷
|
2卷引用:江苏省盐城市2021-2022学年高一上学期期末数学试题
名校
10 . 函数 满足
满足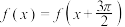 且
且 ,则称函数
,则称函数 为M函数.当
为M函数.当 时,
时, ,
,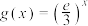 ,且
,且 ,
, 均为M函数,则方程
均为M函数,则方程 在区间
在区间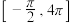 上所有根的和为
上所有根的和为______ .(参考数据: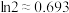 ,
,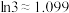 )
)
 满足
满足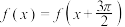 且
且 ,则称函数
,则称函数 为M函数.当
为M函数.当 时,
时, ,
,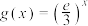 ,且
,且 ,
, 均为M函数,则方程
均为M函数,则方程 在区间
在区间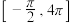 上所有根的和为
上所有根的和为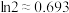 ,
,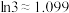 )
)
您最近一年使用:0次
2022-01-26更新
|
537次组卷
|
3卷引用:江苏省扬州中学2021-2022学年高一下学期开学考试数学试题



