名校
解题方法
1 . 设函数 ,
, .记
.记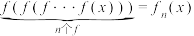 ,
, ,
, .对于D的非空子集A,若对任意
.对于D的非空子集A,若对任意 ,都有
,都有 ,则称函数
,则称函数 在集合A上封闭.
在集合A上封闭.
(1)若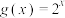 ,
, ,
,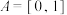 ,分别判断函数
,分别判断函数 和
和 是否在集合A上封闭;
是否在集合A上封闭;
(2)设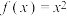 ,
, ,区间
,区间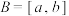 (其中
(其中 ),若函数
),若函数 在集合B上封闭,求
在集合B上封闭,求 的最大值;
的最大值;
(3)设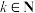 ,
,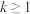 ,若函数
,若函数 的定义域为
的定义域为 ,函数
,函数 和
和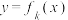 的图象都是连续的曲线,且函数
的图象都是连续的曲线,且函数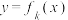 在区间
在区间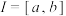 (其中
(其中 )上封闭,证明:存在
)上封闭,证明:存在 ,使得
,使得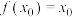 .
.
 ,
, .记
.记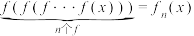 ,
, ,
, .对于D的非空子集A,若对任意
.对于D的非空子集A,若对任意 ,都有
,都有 ,则称函数
,则称函数 在集合A上封闭.
在集合A上封闭.(1)若
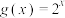 ,
, ,
,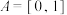 ,分别判断函数
,分别判断函数 和
和 是否在集合A上封闭;
是否在集合A上封闭;(2)设
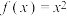 ,
, ,区间
,区间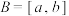 (其中
(其中 ),若函数
),若函数 在集合B上封闭,求
在集合B上封闭,求 的最大值;
的最大值;(3)设
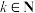 ,
,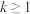 ,若函数
,若函数 的定义域为
的定义域为 ,函数
,函数 和
和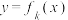 的图象都是连续的曲线,且函数
的图象都是连续的曲线,且函数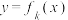 在区间
在区间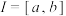 (其中
(其中 )上封闭,证明:存在
)上封闭,证明:存在 ,使得
,使得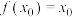 .
.
您最近一年使用:0次
名校
2 . 已知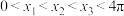 ,函数
,函数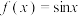 在点
在点 处的切线均经过坐标原点,则( )
处的切线均经过坐标原点,则( )
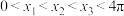 ,函数
,函数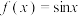 在点
在点 处的切线均经过坐标原点,则( )
处的切线均经过坐标原点,则( )A.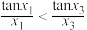 | B.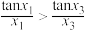 | C.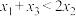 | D.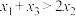 |
您最近一年使用:0次
2024-02-04更新
|
3201次组卷
|
8卷引用:上海市浦东新区上海实验学校2024届高三下学期开学考试数学试题
上海市浦东新区上海实验学校2024届高三下学期开学考试数学试题浙江省温州市2024届高三上学期期末考试数学试题湖南省2024届高三数学新改革提高训练五(九省联考题型)安徽省阜阳市阜阳一中2023-2024学年高二下学期开学检测数学试题(已下线)新题型01 新高考新结构二十一大考点汇总-3(已下线)黄金卷02(2024新题型)甘肃省兰州市西北师范大学附属中学2024届高三第三次诊断考试数学试题辽宁省IC联盟高二下学期6月阶段性质量检测数学试题
名校
3 . 若对任意的 在区间
在区间 上不存在最小值,且对任意正整数n,当
上不存在最小值,且对任意正整数n,当 时有
时有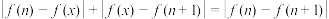 ,
,
(1)比较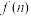 与
与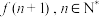 的大小关系;
的大小关系;
(2)判断 是否为
是否为 上的增函数,并说明理由;
上的增函数,并说明理由;
(3)证明:当 时,
时,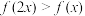 .
.
 在区间
在区间 上不存在最小值,且对任意正整数n,当
上不存在最小值,且对任意正整数n,当 时有
时有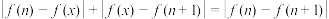 ,
,(1)比较
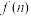 与
与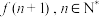 的大小关系;
的大小关系;(2)判断
 是否为
是否为 上的增函数,并说明理由;
上的增函数,并说明理由;(3)证明:当
 时,
时,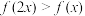 .
.
您最近一年使用:0次
名校
解题方法
4 . 设函数 的定义域为
的定义域为 ,给定区间
,给定区间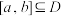 ,若存在
,若存在 ,使得
,使得 ,则称函数
,则称函数 为区间
为区间 上的“均值函数”,
上的“均值函数”, 为函数
为函数 的“均值点”.
的“均值点”.
(1)试判断函数 是否为区间
是否为区间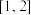 上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
(2)已知函数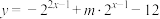 是区间
是区间 上的“均值函数”,求实数
上的“均值函数”,求实数 的取值范围;
的取值范围;
(3)若函数 (常数
(常数 )是区间
)是区间 上的“均值函数”,且
上的“均值函数”,且 为其“均值点”.将区间
为其“均值点”.将区间 任意划分成
任意划分成 (
(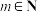 )份,设分点的横坐标从小到大依次为
)份,设分点的横坐标从小到大依次为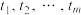 ,记
,记 ,
,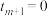 ,
, .再将区间
.再将区间 等分成
等分成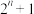 (
( )份,设等分点的横坐标从小到大依次为
)份,设等分点的横坐标从小到大依次为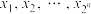 ,记
,记 .求使得
.求使得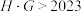 的最小整数
的最小整数 的值.
的值.
 的定义域为
的定义域为 ,给定区间
,给定区间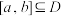 ,若存在
,若存在 ,使得
,使得 ,则称函数
,则称函数 为区间
为区间 上的“均值函数”,
上的“均值函数”, 为函数
为函数 的“均值点”.
的“均值点”.(1)试判断函数
 是否为区间
是否为区间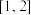 上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;
上的“均值函数”,如果是,请求出其“均值点”;如果不是,请说明理由;(2)已知函数
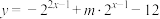 是区间
是区间 上的“均值函数”,求实数
上的“均值函数”,求实数 的取值范围;
的取值范围;(3)若函数
 (常数
(常数 )是区间
)是区间 上的“均值函数”,且
上的“均值函数”,且 为其“均值点”.将区间
为其“均值点”.将区间 任意划分成
任意划分成 (
(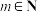 )份,设分点的横坐标从小到大依次为
)份,设分点的横坐标从小到大依次为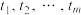 ,记
,记 ,
,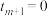 ,
, .再将区间
.再将区间 等分成
等分成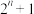 (
( )份,设等分点的横坐标从小到大依次为
)份,设等分点的横坐标从小到大依次为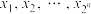 ,记
,记 .求使得
.求使得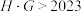 的最小整数
的最小整数 的值.
的值.
您最近一年使用:0次
2023-12-14更新
|
725次组卷
|
5卷引用:上海市金山区2024届高三上学期质量监控数学试题
上海市金山区2024届高三上学期质量监控数学试题(已下线)专题09 导数(三大类型题)15区新题速递(已下线)专题03 函数(三大类型题)15区新题速递广东省广州市第二中学2023-2024学年高二下学期期中考试数学试题福建省泉州实验中学2024-2025学年高三上学期10月月考数学试题
5 . 已知 与
与 都是定义在
都是定义在 上的函数,若对任意
上的函数,若对任意 ,
,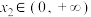 ,当
,当 时,都有
时,都有 ,则称
,则称 是
是 的一个“控制函数”.
的一个“控制函数”.
(1)判断 是否为函数
是否为函数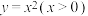 的一个控制函数,并说明理由;
的一个控制函数,并说明理由;
(2)设 的导数为
的导数为 ,
, ,求证:关于
,求证:关于 的方程
的方程 在区间
在区间 上有实数解;
上有实数解;
(3)设 ,函数
,函数 是否存在控制函数?若存在,请求出
是否存在控制函数?若存在,请求出 的所有控制函数;若不存在,请说明理由.
的所有控制函数;若不存在,请说明理由.
 与
与 都是定义在
都是定义在 上的函数,若对任意
上的函数,若对任意 ,
,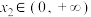 ,当
,当 时,都有
时,都有 ,则称
,则称 是
是 的一个“控制函数”.
的一个“控制函数”.(1)判断
 是否为函数
是否为函数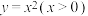 的一个控制函数,并说明理由;
的一个控制函数,并说明理由;(2)设
 的导数为
的导数为 ,
, ,求证:关于
,求证:关于 的方程
的方程 在区间
在区间 上有实数解;
上有实数解;(3)设
 ,函数
,函数 是否存在控制函数?若存在,请求出
是否存在控制函数?若存在,请求出 的所有控制函数;若不存在,请说明理由.
的所有控制函数;若不存在,请说明理由.
您最近一年使用:0次
名校
6 . 已知函数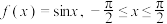 ,
,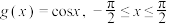 ,下列四个结论中,
,下列四个结论中,正确 的结论有( )
①方程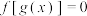 有2个不同的实数解;
有2个不同的实数解;
②方程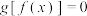 有2个不同的实数解;
有2个不同的实数解;
③方程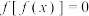 有且只有1个实数解;
有且只有1个实数解;
④当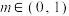 时,方程
时,方程 有2个不同的实数解.
有2个不同的实数解.
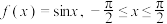 ,
,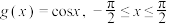 ,下列四个结论中,
,下列四个结论中,①方程
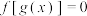 有2个不同的实数解;
有2个不同的实数解;②方程
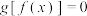 有2个不同的实数解;
有2个不同的实数解;③方程
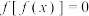 有且只有1个实数解;
有且只有1个实数解;④当
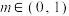 时,方程
时,方程 有2个不同的实数解.
有2个不同的实数解.| A.0个 | B.1个 | C.2个 | D.3个 |
您最近一年使用:0次
名校
解题方法
7 . 已知函数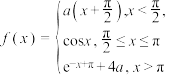 给出下列四个结论:
给出下列四个结论:
①若 有最小值,则
有最小值,则 的取值范围是
的取值范围是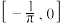 ;
;
②当 时,若
时,若 无实根,则
无实根,则 的取值范围是
的取值范围是 ;
;
③当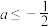 时,不等式
时,不等式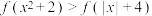 的解集为
的解集为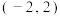 ;
;
④当 时,若存在
时,若存在 ,满足
,满足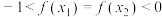 ,则
,则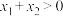 .
.
其中,所有正确结论的序号为__________ .
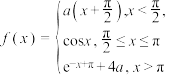 给出下列四个结论:
给出下列四个结论:①若
 有最小值,则
有最小值,则 的取值范围是
的取值范围是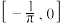 ;
;②当
 时,若
时,若 无实根,则
无实根,则 的取值范围是
的取值范围是 ;
;③当
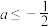 时,不等式
时,不等式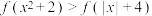 的解集为
的解集为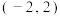 ;
;④当
 时,若存在
时,若存在 ,满足
,满足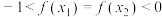 ,则
,则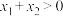 .
.其中,所有正确结论的序号为
您最近一年使用:0次
2023-11-02更新
|
1131次组卷
|
6卷引用:上海市实验学校2023-2024学年高三下学期四模数学试题
8 . 对于函数 ,若实数
,若实数 满足
满足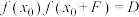 ,其中F、D为非零实数,则
,其中F、D为非零实数,则 称为函数
称为函数 的“
的“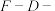 笃志点”.
笃志点”.
(1)若 ,求函数
,求函数 的“
的“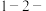 笃志点”;
笃志点”;
(2)已知函数 ,且函数
,且函数 有且只有3个“
有且只有3个“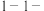 笃志点”,求实数a的取值范围;
笃志点”,求实数a的取值范围;
(3)定义在R上的函数 满足:存在唯一实数m,对任意的实数x,使得
满足:存在唯一实数m,对任意的实数x,使得 恒成立或
恒成立或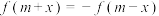 恒成立.对于有序实数对
恒成立.对于有序实数对 ,讨论函数
,讨论函数 “
“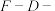 笃志点”个数的奇偶性,并说明理由.
笃志点”个数的奇偶性,并说明理由.
 ,若实数
,若实数 满足
满足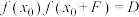 ,其中F、D为非零实数,则
,其中F、D为非零实数,则 称为函数
称为函数 的“
的“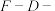 笃志点”.
笃志点”.(1)若
 ,求函数
,求函数 的“
的“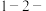 笃志点”;
笃志点”;(2)已知函数
 ,且函数
,且函数 有且只有3个“
有且只有3个“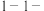 笃志点”,求实数a的取值范围;
笃志点”,求实数a的取值范围;(3)定义在R上的函数
 满足:存在唯一实数m,对任意的实数x,使得
满足:存在唯一实数m,对任意的实数x,使得 恒成立或
恒成立或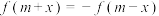 恒成立.对于有序实数对
恒成立.对于有序实数对 ,讨论函数
,讨论函数 “
“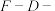 笃志点”个数的奇偶性,并说明理由.
笃志点”个数的奇偶性,并说明理由.
您最近一年使用:0次
2023-10-26更新
|
774次组卷
|
2卷引用:上海市复旦大学附属中学2024届高三上学期10月月考数学试题
名校
9 . 已知函数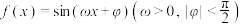 的图象相邻两条对称轴间的距离为
的图象相邻两条对称轴间的距离为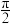 ,且过点
,且过点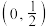 .
.
(1)若函数 是偶函数,求
是偶函数,求 的最小值;
的最小值;
(2)令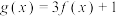 ,记函数
,记函数 在
在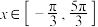 上的零点从小到大依次为
上的零点从小到大依次为 、
、 、
、 、
、 ,求
,求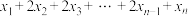 的值;
的值;
(3)设函数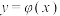 ,
, ,如果对于定义域D内的任意实数
,如果对于定义域D内的任意实数 ,对于给定的非零常数
,对于给定的非零常数 ,总存在非零常数
,总存在非零常数 ,若恒有
,若恒有 成立,则称函数
成立,则称函数 是
是 上的
上的 级周期函数,周期为
级周期函数,周期为 .是否存在非零实数
.是否存在非零实数 ,使函数
,使函数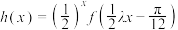 是
是 上的周期为
上的周期为 的
的 级周期函数?请证明你的结论.
级周期函数?请证明你的结论.
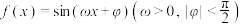 的图象相邻两条对称轴间的距离为
的图象相邻两条对称轴间的距离为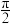 ,且过点
,且过点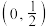 .
.(1)若函数
 是偶函数,求
是偶函数,求 的最小值;
的最小值;(2)令
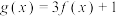 ,记函数
,记函数 在
在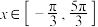 上的零点从小到大依次为
上的零点从小到大依次为 、
、 、
、 、
、 ,求
,求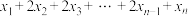 的值;
的值;(3)设函数
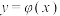 ,
, ,如果对于定义域D内的任意实数
,如果对于定义域D内的任意实数 ,对于给定的非零常数
,对于给定的非零常数 ,总存在非零常数
,总存在非零常数 ,若恒有
,若恒有 成立,则称函数
成立,则称函数 是
是 上的
上的 级周期函数,周期为
级周期函数,周期为 .是否存在非零实数
.是否存在非零实数 ,使函数
,使函数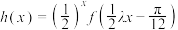 是
是 上的周期为
上的周期为 的
的 级周期函数?请证明你的结论.
级周期函数?请证明你的结论.
您最近一年使用:0次
2023-06-16更新
|
563次组卷
|
4卷引用:【巩固卷】期中测评卷 单元测试A-沪教版(2020)必修第二册
名校
10 . 已知关于 的方程
的方程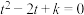 (
( 为常数且
为常数且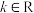 )的一个根为
)的一个根为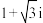 (i为虚数单位),关于
(i为虚数单位),关于 的函数
的函数 的图象与坐标轴恰有2个交点,则实数
的图象与坐标轴恰有2个交点,则实数 值为
值为______ .
 的方程
的方程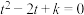 (
( 为常数且
为常数且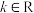 )的一个根为
)的一个根为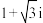 (i为虚数单位),关于
(i为虚数单位),关于 的函数
的函数 的图象与坐标轴恰有2个交点,则实数
的图象与坐标轴恰有2个交点,则实数 值为
值为
您最近一年使用:0次



