1 . 已知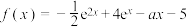 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 有两个极值点
有两个极值点 ,
, ,证明:
,证明: .
.
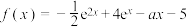 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若
 有两个极值点
有两个极值点 ,
, ,证明:
,证明: .
.
您最近半年使用:0次
解题方法
2 . 已知函数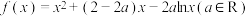 .
.
(1)若 ,求
,求 的极值;
的极值;
(2)若 ,求证:
,求证: .
.
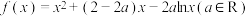 .
.(1)若
 ,求
,求 的极值;
的极值;(2)若
 ,求证:
,求证: .
.
您最近半年使用:0次
3 . 已知 ,函数
,函数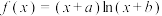 的图象在点
的图象在点 处的切线方程为
处的切线方程为 .
.
(1)求a,b的值;
(2)若方程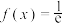 (e为自然对数的底数)有两个实数根
(e为自然对数的底数)有两个实数根 ,且
,且 ,证明:
,证明: 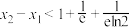
 ,函数
,函数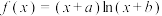 的图象在点
的图象在点 处的切线方程为
处的切线方程为 .
.(1)求a,b的值;
(2)若方程
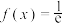 (e为自然对数的底数)有两个实数根
(e为自然对数的底数)有两个实数根 ,且
,且 ,证明:
,证明: 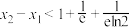
您最近半年使用:0次
2024高三·全国·专题练习
4 . 已知函数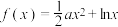 .
.
(1)若函数 在
在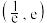 上有两个零点,求实数a的取值范围;
上有两个零点,求实数a的取值范围;
(2)证明:对任意的正整数n,不等式 都成立.
都成立.
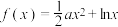 .
.(1)若函数
 在
在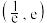 上有两个零点,求实数a的取值范围;
上有两个零点,求实数a的取值范围;(2)证明:对任意的正整数n,不等式
 都成立.
都成立.
您最近半年使用:0次
解题方法
5 . 已知函数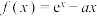 ,
, .
.
(1)若曲线 在
在 处的切线的斜率为2,求
处的切线的斜率为2,求 的值;
的值;
(2)当 时,证明:
时,证明: ,
, ;
;
(3)若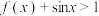 在区间
在区间 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
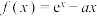 ,
, .
.(1)若曲线
 在
在 处的切线的斜率为2,求
处的切线的斜率为2,求 的值;
的值;(2)当
 时,证明:
时,证明: ,
, ;
;(3)若
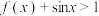 在区间
在区间 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
您最近半年使用:0次
2024·全国·模拟预测
6 . 已知函数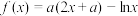 .
.
(1)讨论 的单调性;
的单调性;
(2)证明:当 时,
时,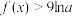 .(参考数据:
.(参考数据: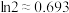 )
)
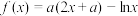 .
.(1)讨论
 的单调性;
的单调性;(2)证明:当
 时,
时,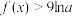 .(参考数据:
.(参考数据: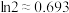 )
)
您最近半年使用:0次
名校
解题方法
7 . 已知函数 .
.
(1)若 ,证明:
,证明: ;
;
(2)若函数 在
在 内有唯一零点,求实数
内有唯一零点,求实数 的取值范围.
的取值范围.
 .
.(1)若
 ,证明:
,证明: ;
;(2)若函数
 在
在 内有唯一零点,求实数
内有唯一零点,求实数 的取值范围.
的取值范围.
您最近半年使用:0次
解题方法
8 . 已知函数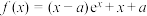 (
(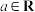 ).
).
(1)若 ,求
,求 的图象在
的图象在 处的切线方程;
处的切线方程;
(2)若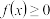 对于任意的
对于任意的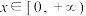 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)若数列 满足
满足 且
且 (
(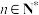 ),记数列
),记数列 的前n项和为
的前n项和为 ,求证:
,求证: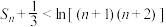 .
.
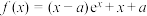 (
(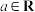 ).
).(1)若
 ,求
,求 的图象在
的图象在 处的切线方程;
处的切线方程;(2)若
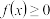 对于任意的
对于任意的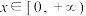 恒成立,求a的取值范围;
恒成立,求a的取值范围;(3)若数列
 满足
满足 且
且 (
(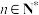 ),记数列
),记数列 的前n项和为
的前n项和为 ,求证:
,求证: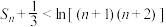 .
.
您最近半年使用:0次
2024-05-01更新
|
735次组卷
|
3卷引用:山西省晋城市2024届高三第二次模拟考试数学试题
解题方法
9 . 已知常数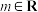 ,设
,设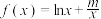 ,
,
(1)若 ,求函数
,求函数 的最小值;
的最小值;
(2)是否存在 ,且
,且 ,
, ,
, 依次成等比数列,使得
依次成等比数列,使得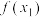 、
、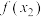 、
、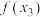 依次成等差数列?请说明理由.
依次成等差数列?请说明理由.
(3)求证:“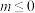 ”是“对任意
”是“对任意 ,
, ,都有
,都有 ”的充要条件.
”的充要条件.
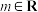 ,设
,设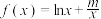 ,
,(1)若
 ,求函数
,求函数 的最小值;
的最小值;(2)是否存在
 ,且
,且 ,
, ,
, 依次成等比数列,使得
依次成等比数列,使得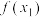 、
、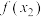 、
、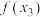 依次成等差数列?请说明理由.
依次成等差数列?请说明理由.(3)求证:“
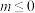 ”是“对任意
”是“对任意 ,
, ,都有
,都有 ”的充要条件.
”的充要条件.
您最近半年使用:0次
名校
10 . 已知函数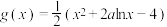 .
.
(1)讨论函数 的单调性;
的单调性;
(2)设函数 ,若函数
,若函数 的导函数有两个不同的零点
的导函数有两个不同的零点 ,
,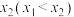 ,证明:
,证明: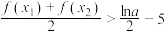 .
.
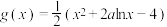 .
.(1)讨论函数
 的单调性;
的单调性;(2)设函数
 ,若函数
,若函数 的导函数有两个不同的零点
的导函数有两个不同的零点 ,
,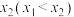 ,证明:
,证明: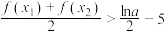 .
.
您最近半年使用:0次



