名校
1 . 设等比数列 的前
的前 项和为
项和为 ,则“数列
,则“数列 为递增数列”是“
为递增数列”是“ ”的( )
”的( )
 的前
的前 项和为
项和为 ,则“数列
,则“数列 为递增数列”是“
为递增数列”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
7日内更新
|
608次组卷
|
3卷引用:天津市第四中学2025届高三上学期统练(二)数学试题
名校
2 . 已知等比数列 的前n项和为
的前n项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与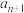 之间插入n个数,使这
之间插入n个数,使这 个数组成一个公差为
个数组成一个公差为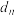 的等差数列.
的等差数列.
(i)求数列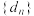 的通项及
的通项及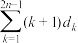 ;
;
(ii)在数列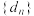 中是否存在3项
中是否存在3项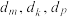 (其中m,k,p成等差数列)成等比数列?若存在,求出这样的3项;若不存在,请说明理由.
(其中m,k,p成等差数列)成等比数列?若存在,求出这样的3项;若不存在,请说明理由.
 的前n项和为
的前n项和为 ,且
,且 .
.(1)求数列
 的通项公式;
的通项公式;(2)在
 与
与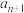 之间插入n个数,使这
之间插入n个数,使这 个数组成一个公差为
个数组成一个公差为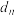 的等差数列.
的等差数列.(i)求数列
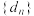 的通项及
的通项及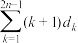 ;
;(ii)在数列
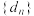 中是否存在3项
中是否存在3项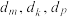 (其中m,k,p成等差数列)成等比数列?若存在,求出这样的3项;若不存在,请说明理由.
(其中m,k,p成等差数列)成等比数列?若存在,求出这样的3项;若不存在,请说明理由.
您最近一年使用:0次
3 . 南宋数学家杨辉为我国古代数学研究做出了杰出贡献,他的著名研究成果“杨辉三角”记录于其重要著作《详解九章算法》,该著作中的“垛积术”问题介绍了高阶等差数列,以高阶等差数列中的二阶等差数列为例,其特点是从数列的第二项开始,每一项与前一项的差构成等差数列.若某个二阶等差数列的前4项为1,3,7,13,则该数列的第15项为______ .
您最近一年使用:0次
2024-10-13更新
|
227次组卷
|
2卷引用:天津市新华中学2024-2025学年高三上学期第一次月考数学试卷
4 . 已知数列 的前
的前 项和为
项和为 ,满足
,满足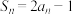 ,
,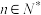 .数列
.数列 满足
满足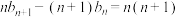 ,
,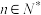 ,且
,且 .
.
(1)证明数列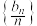 为等差数列,并求数列
为等差数列,并求数列 和
和 的通项公式;
的通项公式;
(2)若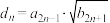 ,数列
,数列 的前
的前 项和为
项和为 ,对任意的
,对任意的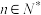 ,都有
,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)记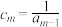 ,
,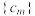 的前
的前 项和记为
项和记为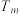 ,是否存在
,是否存在 ,
,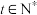 ,使得
,使得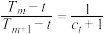 成立?若存在,求出
成立?若存在,求出 ,
, 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的前
的前 项和为
项和为 ,满足
,满足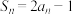 ,
,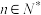 .数列
.数列 满足
满足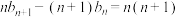 ,
,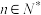 ,且
,且 .
.(1)证明数列
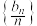 为等差数列,并求数列
为等差数列,并求数列 和
和 的通项公式;
的通项公式;(2)若
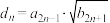 ,数列
,数列 的前
的前 项和为
项和为 ,对任意的
,对任意的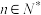 ,都有
,都有 ,求实数
,求实数 的取值范围;
的取值范围;(3)记
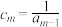 ,
,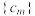 的前
的前 项和记为
项和记为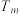 ,是否存在
,是否存在 ,
,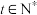 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 ,
, 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
5 . 已知数列 满足:
满足: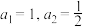 ,且
,且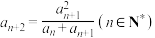 ,则数列
,则数列 的通项公式是
的通项公式是______________
 满足:
满足: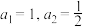 ,且
,且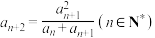 ,则数列
,则数列 的通项公式是
的通项公式是
您最近一年使用:0次
2024-10-12更新
|
659次组卷
|
2卷引用:天津市耀华中学2025届高三上学期第一次月考数学试卷
名校
6 . 设 是等比数列,
是等比数列, 是递增的等差数列,
是递增的等差数列, 的前
的前 项和为
项和为 (
( ),
), ,
, ,
,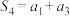 ,
,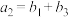 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)将数列 与数列
与数列 的所有项按照从小到大的顺序排列成一个新的数列,求此新数列的前
的所有项按照从小到大的顺序排列成一个新的数列,求此新数列的前 项和;
项和;
(3) 表示不超过
表示不超过 的最大整数,
的最大整数, 表示数列
表示数列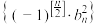 的前
的前 项和,集合
项和,集合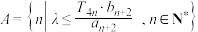 共有4个元素,求
共有4个元素,求 范围.
范围.
 是等比数列,
是等比数列, 是递增的等差数列,
是递增的等差数列, 的前
的前 项和为
项和为 (
( ),
), ,
, ,
,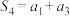 ,
,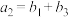 .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)将数列
 与数列
与数列 的所有项按照从小到大的顺序排列成一个新的数列,求此新数列的前
的所有项按照从小到大的顺序排列成一个新的数列,求此新数列的前 项和;
项和;(3)
 表示不超过
表示不超过 的最大整数,
的最大整数, 表示数列
表示数列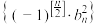 的前
的前 项和,集合
项和,集合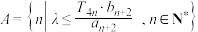 共有4个元素,求
共有4个元素,求 范围.
范围.
您最近一年使用:0次
名校
解题方法
7 . 已知数列 满足:
满足: ,且
,且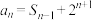 ,其中
,其中 为
为 的前
的前 项和.
项和.
(1)令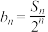 ,求证:
,求证: 为等差数列;
为等差数列;
(2)求 的通项公式.
的通项公式.
 满足:
满足: ,且
,且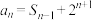 ,其中
,其中 为
为 的前
的前 项和.
项和.(1)令
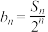 ,求证:
,求证: 为等差数列;
为等差数列;(2)求
 的通项公式.
的通项公式.
您最近一年使用:0次
8 . 已知数列 ,
,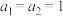 ,
, .
.
(1)证明:数列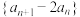 ,
, 为等比数列;
为等比数列;
(2)求数列 的通项公式;
的通项公式;
(3)求数列 的前n项和
的前n项和 .
.
 ,
,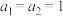 ,
, .
.(1)证明:数列
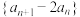 ,
, 为等比数列;
为等比数列;(2)求数列
 的通项公式;
的通项公式;(3)求数列
 的前n项和
的前n项和 .
.
您最近一年使用:0次
2024-10-09更新
|
1091次组卷
|
2卷引用:天津市双菱中学2025届高三上学期第一次月考数学试卷
2024高二·全国·专题练习
名校
9 . 已知数列 的通项公式为
的通项公式为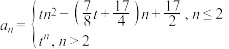 ,且对任意的两个正整数
,且对任意的两个正整数 ,
,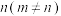 都有
都有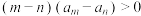 ,则实数t的取值范围是( )
,则实数t的取值范围是( )
 的通项公式为
的通项公式为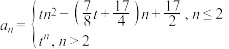 ,且对任意的两个正整数
,且对任意的两个正整数 ,
,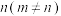 都有
都有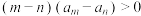 ,则实数t的取值范围是( )
,则实数t的取值范围是( )A.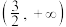 | B.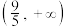 | C. | D.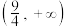 |
您最近一年使用:0次
解题方法
10 . 已知数列 满足
满足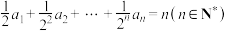 ,则数列
,则数列 的通项公式为
的通项公式为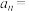
______ ,若数列 的前
的前 项和为
项和为 ,记
,记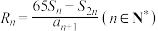 ,则数列
,则数列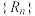 的最大项为第
的最大项为第______ 项.
 满足
满足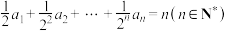 ,则数列
,则数列 的通项公式为
的通项公式为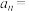
 的前
的前 项和为
项和为 ,记
,记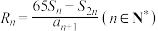 ,则数列
,则数列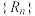 的最大项为第
的最大项为第
您最近一年使用:0次



