1 . 现将一个高为4,体积为 的圆柱削成一个空间几何体ABCD,其中棱AB,CD分别为圆柱上、下底面上相互垂直的两条直径,则被削去部分的体积为
的圆柱削成一个空间几何体ABCD,其中棱AB,CD分别为圆柱上、下底面上相互垂直的两条直径,则被削去部分的体积为______ .
 的圆柱削成一个空间几何体ABCD,其中棱AB,CD分别为圆柱上、下底面上相互垂直的两条直径,则被削去部分的体积为
的圆柱削成一个空间几何体ABCD,其中棱AB,CD分别为圆柱上、下底面上相互垂直的两条直径,则被削去部分的体积为
您最近一年使用:0次
2 . 楔体形构件在建筑工程上有广泛的应用.如图,某楔体形构件可视为一个五面体 ,其中面
,其中面 为正方形.若
为正方形.若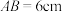 ,
, ,且
,且 与面
与面 的距离为
的距离为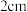 ,则该楔体形构件的体积为( )
,则该楔体形构件的体积为( )
 ,其中面
,其中面 为正方形.若
为正方形.若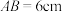 ,
, ,且
,且 与面
与面 的距离为
的距离为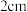 ,则该楔体形构件的体积为( )
,则该楔体形构件的体积为( )
A.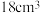 | B. | C. | D.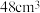 |
您最近一年使用:0次
2024·河北邢台·二模
名校
解题方法
3 . 如图,四边形 和
和 是两个相同的矩形,面积均为300,图中阴影部分也是四个相同的矩形,现将阴影部分分别沿
是两个相同的矩形,面积均为300,图中阴影部分也是四个相同的矩形,现将阴影部分分别沿 ,
,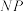 ,
, ,
,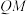 折起,得到一个无盖长方体,则该长方体体积的最大值为
折起,得到一个无盖长方体,则该长方体体积的最大值为________ .
 和
和 是两个相同的矩形,面积均为300,图中阴影部分也是四个相同的矩形,现将阴影部分分别沿
是两个相同的矩形,面积均为300,图中阴影部分也是四个相同的矩形,现将阴影部分分别沿 ,
,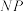 ,
, ,
,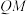 折起,得到一个无盖长方体,则该长方体体积的最大值为
折起,得到一个无盖长方体,则该长方体体积的最大值为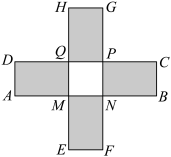
您最近一年使用:0次
2024·湖南常德·三模
解题方法
4 . 如图,现有棱长为6cm的正方体玉石缺失了一个角,缺失部分为正三棱锥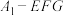 ,且
,且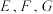 分别为棱
分别为棱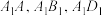 靠近
靠近 的四等分点,若将该玉石打磨成一个球形饰品,则该球形饰品的体积的最大值为( )
的四等分点,若将该玉石打磨成一个球形饰品,则该球形饰品的体积的最大值为( )
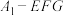 ,且
,且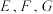 分别为棱
分别为棱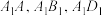 靠近
靠近 的四等分点,若将该玉石打磨成一个球形饰品,则该球形饰品的体积的最大值为( )
的四等分点,若将该玉石打磨成一个球形饰品,则该球形饰品的体积的最大值为( )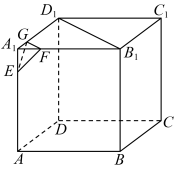
A.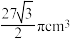 | B.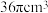 |
C.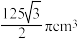 | D.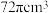 |
您最近一年使用:0次
5 . 如图,四面体 中,
中,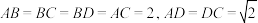 .
.
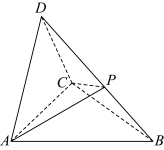
(1)求证:平面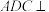 平面
平面 ;
;
(2)若 ,
,
①若直线 与平面
与平面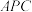 所成角为30°,求
所成角为30°,求 的值;
的值;
②若 平面
平面 为垂足,直线
为垂足,直线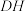 与平面
与平面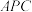 的交点为
的交点为 .当三棱锥
.当三棱锥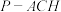 体积最大时,求
体积最大时,求 的值.
的值.
 中,
中,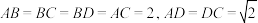 .
.
(1)求证:平面
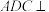 平面
平面 ;
;(2)若
 ,
,①若直线
 与平面
与平面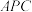 所成角为30°,求
所成角为30°,求 的值;
的值;②若
 平面
平面 为垂足,直线
为垂足,直线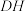 与平面
与平面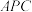 的交点为
的交点为 .当三棱锥
.当三棱锥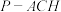 体积最大时,求
体积最大时,求 的值.
的值.
您最近一年使用:0次
2024-04-27更新
|
572次组卷
|
3卷引用:江苏高二专题02立体几何与空间向量(第二部分)
江苏高二专题02立体几何与空间向量(第二部分)江苏省南京市五所高中学校合作联盟2023-2024学年高二下学期期中学情调研数学试卷(已下线)模块三 专题2 解答题分类练 专题3 空间向量线性运算(苏教版)
2024·浙江嘉兴·二模
6 . 如图,这是一个水上漂浮式警示浮标,它的主体由上面一个圆锥和下面一个半球体组成.已知该浮标上面圆锥的侧面积是下面半球面面积的2倍,则圆锥的体积与半球体的体积的比值为( )

A.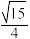 | B. | C. | D.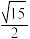 |
您最近一年使用:0次
2024高三·全国·专题练习
7 . 在一个透明的正四棱柱形状的容器中,盛上一些水,只固定容器底面的一个顶点,容器位置自由倾斜,观察水的表面的形状、面积大小的变化,试指出各种变化的情形及各种量之间可能存在的关系.
您最近一年使用:0次
2024高三·全国·专题练习
解题方法
8 . 四面体三组对棱长分别为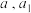 ;
;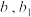 ;
; ,证明:四面体的内切球半径
,证明:四面体的内切球半径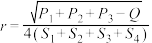 .
.
(其中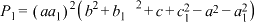 ,
,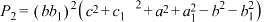 ,
,
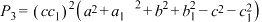 ,
,
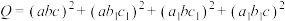 ,
,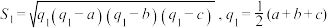 ,
,
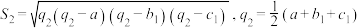 ,
,
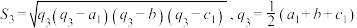 ,
,
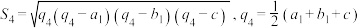 .)
.)
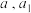 ;
;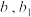 ;
; ,证明:四面体的内切球半径
,证明:四面体的内切球半径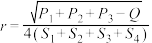 .
.(其中
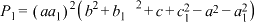 ,
,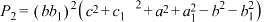 ,
,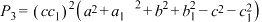 ,
,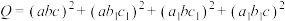 ,
,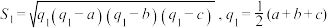 ,
,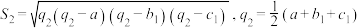 ,
,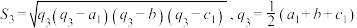 ,
,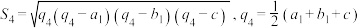 .)
.)
您最近一年使用:0次
9 . 设球的半径为 ,试根据祖暅原理设计一个与球体积相等的四棱锥.
,试根据祖暅原理设计一个与球体积相等的四棱锥.
 ,试根据祖暅原理设计一个与球体积相等的四棱锥.
,试根据祖暅原理设计一个与球体积相等的四棱锥.
您最近一年使用:0次

 的内接三棱锥,其底面三角形的两个内角分别为
的内接三棱锥,其底面三角形的两个内角分别为 ,求圆锥的体积.
,求圆锥的体积.


