名校
1 . 如图,在平行六面体 中,设
中,设 ,
,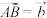 ,
, ,
, ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,试用
的中点,试用 ,
, ,
, 表示以下各向量:
表示以下各向量:
(2)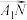
(3) .
.
 中,设
中,设 ,
,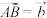 ,
, ,
, ,
, ,
, 分别是棱
分别是棱 ,
, ,
, 的中点,试用
的中点,试用 ,
, ,
, 表示以下各向量:
表示以下各向量: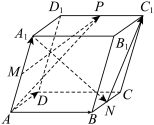

(2)
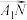
(3)
 .
.
您最近半年使用:0次
解题方法
2 . 如图,在底面 为菱形的平行六面体
为菱形的平行六面体 中,
中, 分别在棱
分别在棱 上,且
上,且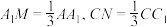 ,且
,且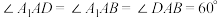 .
.
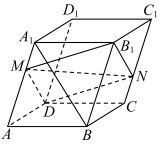
(1)求证: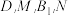 共面;
共面;
(2)当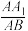 为何值时,
为何值时,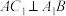 ;
;
(3)若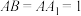 ,且
,且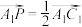 ,求
,求 的长.
的长.
 为菱形的平行六面体
为菱形的平行六面体 中,
中, 分别在棱
分别在棱 上,且
上,且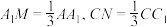 ,且
,且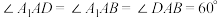 .
.
(1)求证:
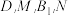 共面;
共面;(2)当
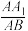 为何值时,
为何值时,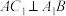 ;
;(3)若
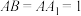 ,且
,且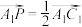 ,求
,求 的长.
的长.
您最近半年使用:0次
2024-04-07更新
|
234次组卷
|
2卷引用:江苏省常州市联盟学校2023-2024学年高二下学期3月阶段调研数学试题
名校
解题方法
3 . 三阶行列式是解决复杂代数运算的算法,其运算法则如下: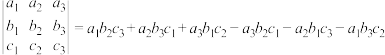
 若
若 ,则称
,则称 为空间向量
为空间向量 与
与 的叉乘,其中
的叉乘,其中 ,
, ,
,  为单位正交基底. 以
为单位正交基底. 以  为坐标原点、分别以
为坐标原点、分别以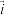 ,
, ,
,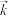 的方向为
的方向为  轴、
轴、  轴、
轴、  轴的正方向建立空间直角坐标系,已知
轴的正方向建立空间直角坐标系,已知 ,
, 是空间直角坐标系中异于
是空间直角坐标系中异于  的不同两点
的不同两点
(1)①若 ,
, ,求
,求 ;
;
②证明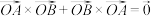 .
.
(2)记 的面积为
的面积为 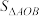 ,证明:
,证明: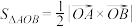 .
.
(3)证明: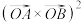 的几何意义表示以
的几何意义表示以 为底面、
为底面、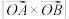 为高的三棱锥体积的
为高的三棱锥体积的 倍.
倍.
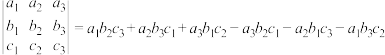
 若
若 ,则称
,则称 为空间向量
为空间向量 与
与 的叉乘,其中
的叉乘,其中 ,
, ,
,  为单位正交基底. 以
为单位正交基底. 以  为坐标原点、分别以
为坐标原点、分别以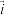 ,
, ,
,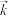 的方向为
的方向为  轴、
轴、  轴、
轴、  轴的正方向建立空间直角坐标系,已知
轴的正方向建立空间直角坐标系,已知 ,
, 是空间直角坐标系中异于
是空间直角坐标系中异于  的不同两点
的不同两点(1)①若
 ,
, ,求
,求 ;
;②证明
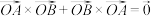 .
.(2)记
 的面积为
的面积为 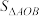 ,证明:
,证明: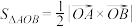 .
.(3)证明:
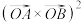 的几何意义表示以
的几何意义表示以 为底面、
为底面、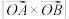 为高的三棱锥体积的
为高的三棱锥体积的 倍.
倍.
您最近半年使用:0次
2024-04-06更新
|
618次组卷
|
7卷引用:河南省部分重点高中2024届高三普通高等学校招生全国统一考试(期末联考)数学试卷
河南省部分重点高中2024届高三普通高等学校招生全国统一考试(期末联考)数学试卷江苏省扬州市仪征中学2024届高三下学期期初调研测试数学试题 河南省部分重点高中(青桐鸣)2023-2024学年高三上学期期末大联考数学试题(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大核心考点)(讲义)江苏省江都中学2023-2024学年高二下学期3月联考数学试卷江苏省盱眙中学2023-2024学年高二下学期第一次学情调研数学试题(已下线)第七章 应用空间向量解立体几何问题拓展 专题二 平面法向量求法及其应用 微点2 平面法向量求法及其应用(二)【培优版】
名校
4 . 如图,三棱锥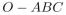 的棱长都相等,记
的棱长都相等,记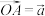 ,
,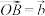 ,
,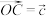 ,点
,点 在棱
在棱 上,
上,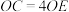 .
.

(1)若D是棱 的三等分点(靠近点
的三等分点(靠近点 ),用向量
),用向量 ,
, ,
, 表示向量
表示向量 ;
;
(2)若D是棱 的中点,
的中点,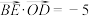 ,求三棱锥的棱长.
,求三棱锥的棱长.
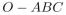 的棱长都相等,记
的棱长都相等,记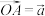 ,
,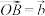 ,
,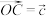 ,点
,点 在棱
在棱 上,
上,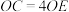 .
.
(1)若D是棱
 的三等分点(靠近点
的三等分点(靠近点 ),用向量
),用向量 ,
, ,
, 表示向量
表示向量 ;
;(2)若D是棱
 的中点,
的中点,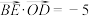 ,求三棱锥的棱长.
,求三棱锥的棱长.
您最近半年使用:0次
2024高三·全国·专题练习
5 . 如图,在平行六面体ABCD-A1B1C1D1中,设AA1=a, =b,
=b,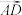 =c,M,N,P分别是AA1,BC,C1D1的中点.试用a,b,c表示以下各向量:
=c,M,N,P分别是AA1,BC,C1D1的中点.试用a,b,c表示以下各向量:

(1)
 ;
;(2)A1N;
(3)
 +NC1.
+NC1.
您最近半年使用:0次
2024高三·全国·专题练习
6 . 如图平行六面体 中,三棱
中,三棱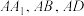 间夹角均为
间夹角均为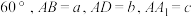 .求:
.求:
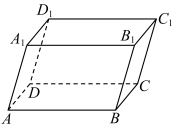
(1)对角线 的长度;
的长度;
(2)平行六面体全面积 ;
;
(3)平行六面体体积 .
.
 中,三棱
中,三棱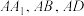 间夹角均为
间夹角均为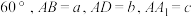 .求:
.求:
(1)对角线
 的长度;
的长度;(2)平行六面体全面积
 ;
;(3)平行六面体体积
 .
.
您最近半年使用:0次
解题方法
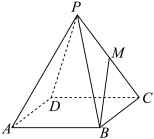
7 . 如图,在四棱锥 中,底面
中,底面 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 的长为1,且
的长为1,且 与
与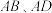 的夹角都等于60°,M在棱
的夹角都等于60°,M在棱 上,
上,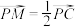 ,设
,设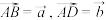 ,
,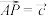 .
.
(1)试用
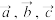 表示出向量
表示出向量 ;
;(2)求
 与
与 所成的角的余弦值.
所成的角的余弦值.
您最近半年使用:0次
名校
8 . 如图所示,平行六面体 中,
中,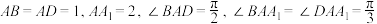 .
.
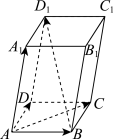
(1)用向量 表示向量
表示向量 ,并求
,并求 ;
;
(2)求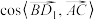 .
.
 中,
中,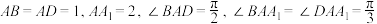 .
.
(1)用向量
 表示向量
表示向量 ,并求
,并求 ;
;(2)求
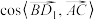 .
.
您最近半年使用:0次
9 . 三阶行列式是解决复杂代数运算的算法,其运算法则如下:
 .若
.若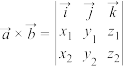 ,则称
,则称 为空间向量
为空间向量 与
与 的叉乘,其中
的叉乘,其中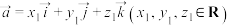 ,
,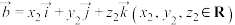 ,
, 为单位正交基底.以
为单位正交基底.以 为坐标原点,分别以
为坐标原点,分别以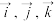 的方向为
的方向为 轴、
轴、 轴、
轴、 轴的正方向建立空间直角坐标系,已知
轴的正方向建立空间直角坐标系,已知 是空间直角坐标系中异于
是空间直角坐标系中异于 的不同两点.
的不同两点.
(1)①若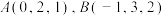 ,求
,求 ;
;
②证明: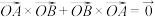 .
.
(2)记 的面积为
的面积为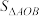 ,证明:
,证明: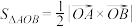 ;
;
(3)问: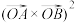 的几何意义表示以
的几何意义表示以 为底面、
为底面、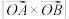 为高的三棱锥体积的多少倍?
为高的三棱锥体积的多少倍?

 .若
.若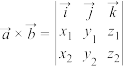 ,则称
,则称 为空间向量
为空间向量 与
与 的叉乘,其中
的叉乘,其中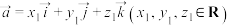 ,
,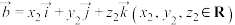 ,
, 为单位正交基底.以
为单位正交基底.以 为坐标原点,分别以
为坐标原点,分别以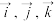 的方向为
的方向为 轴、
轴、 轴、
轴、 轴的正方向建立空间直角坐标系,已知
轴的正方向建立空间直角坐标系,已知 是空间直角坐标系中异于
是空间直角坐标系中异于 的不同两点.
的不同两点.(1)①若
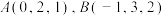 ,求
,求 ;
;②证明:
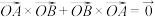 .
.(2)记
 的面积为
的面积为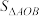 ,证明:
,证明: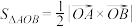 ;
;(3)问:
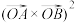 的几何意义表示以
的几何意义表示以 为底面、
为底面、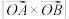 为高的三棱锥体积的多少倍?
为高的三棱锥体积的多少倍?
您最近半年使用:0次

 为直角梯形,
为直角梯形, ,
,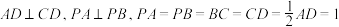 ,设
,设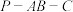 的二面角为
的二面角为
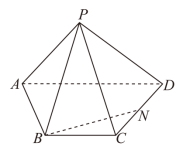
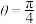 时,求
时,求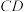 的中点,
的中点,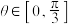 ,求
,求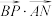 的取值范围.
的取值范围.


