已知 分别为双曲线
分别为双曲线 的左、右支上的点,
的左、右支上的点, 的右焦点为
的右焦点为 为坐标原点.
为坐标原点.
(1)若 三点共线,且
三点共线,且 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.
(2)若直线 与圆
与圆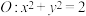 相切,试判断
相切,试判断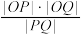 是否为定值.若是,求出该定值;若不是,请说明理由.
是否为定值.若是,求出该定值;若不是,请说明理由.
 分别为双曲线
分别为双曲线 的左、右支上的点,
的左、右支上的点, 的右焦点为
的右焦点为 为坐标原点.
为坐标原点.(1)若
 三点共线,且
三点共线,且 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.(2)若直线
 与圆
与圆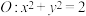 相切,试判断
相切,试判断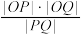 是否为定值.若是,求出该定值;若不是,请说明理由.
是否为定值.若是,求出该定值;若不是,请说明理由.
2024·广东·模拟预测 查看更多[3]
更新时间:2024/03/07 15:12:37
|
相似题推荐
解答题-问答题
|
困难
(0.15)
名校
解题方法
【推荐1】已知双曲线 的离心率为
的离心率为 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在双曲线
在双曲线 的右支上,且
的右支上,且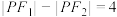 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)过点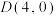 的直线
的直线 交双曲线
交双曲线 于
于 两点,且以
两点,且以 为直径的圆过原点
为直径的圆过原点 ,求弦长
,求弦长 .
.
 的离心率为
的离心率为 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 ,点
,点 在双曲线
在双曲线 的右支上,且
的右支上,且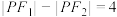 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)过点
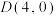 的直线
的直线 交双曲线
交双曲线 于
于 两点,且以
两点,且以 为直径的圆过原点
为直径的圆过原点 ,求弦长
,求弦长 .
.
您最近一年使用:0次
解答题-问答题
|
困难
(0.15)
名校
解题方法
【推荐2】在平面直角坐标系 中,双曲线
中,双曲线 的左顶点到右焦点的距离是
的左顶点到右焦点的距离是 ,且
,且 的离心率是
的离心率是 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)点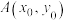 是
是 上位于第一象限的一点,点
上位于第一象限的一点,点 、
、 关于原点
关于原点 对称,点
对称,点 、
、 关于
关于 轴对称.延长
轴对称.延长 至
至 使得
使得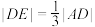 ,且直线
,且直线 和
和 的另一个交点
的另一个交点 位于第二象限中.
位于第二象限中.
(i)求 的取值范围;
的取值范围;
(ii)证明: 不可能是
不可能是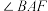 的三等分线.
的三等分线.
 中,双曲线
中,双曲线 的左顶点到右焦点的距离是
的左顶点到右焦点的距离是 ,且
,且 的离心率是
的离心率是 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)点
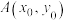 是
是 上位于第一象限的一点,点
上位于第一象限的一点,点 、
、 关于原点
关于原点 对称,点
对称,点 、
、 关于
关于 轴对称.延长
轴对称.延长 至
至 使得
使得 ,且直线
,且直线 和
和 的另一个交点
的另一个交点 位于第二象限中.
位于第二象限中.(i)求
 的取值范围;
的取值范围;(ii)证明:
 不可能是
不可能是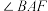 的三等分线.
的三等分线.
您最近一年使用:0次
【推荐1】我们约定,如果一个椭圆的长轴和短轴分别是另一条双曲线的实轴和虚轴,则称它们互为“姊妺”圆锥曲线.已知椭圆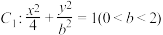 ,双曲线
,双曲线 是椭圆
是椭圆 的“姊妺”圆锥曲线,
的“姊妺”圆锥曲线,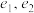 分别为
分别为 的离心率,且
的离心率,且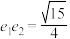 ,点
,点 分别为椭圆
分别为椭圆 的左、右顶点.
的左、右顶点.
(1)求双曲线 的方程;
的方程;
(2)设过点 的动直线
的动直线 交双曲线
交双曲线 右支于
右支于 两点,若直线
两点,若直线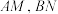 的斜率分别为
的斜率分别为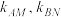 .
.
(i)试探究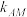 与
与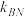 的比值
的比值 是否为定值.若是定值,求出这个定值;若不是定值,请说明理由;
是否为定值.若是定值,求出这个定值;若不是定值,请说明理由;
(ii)求 的取值范围.
的取值范围.
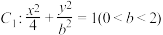 ,双曲线
,双曲线 是椭圆
是椭圆 的“姊妺”圆锥曲线,
的“姊妺”圆锥曲线,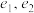 分别为
分别为 的离心率,且
的离心率,且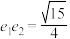 ,点
,点 分别为椭圆
分别为椭圆 的左、右顶点.
的左、右顶点.(1)求双曲线
 的方程;
的方程;(2)设过点
 的动直线
的动直线 交双曲线
交双曲线 右支于
右支于 两点,若直线
两点,若直线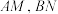 的斜率分别为
的斜率分别为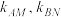 .
.(i)试探究
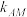 与
与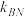 的比值
的比值 是否为定值.若是定值,求出这个定值;若不是定值,请说明理由;
是否为定值.若是定值,求出这个定值;若不是定值,请说明理由;(ii)求
 的取值范围.
的取值范围.
您最近一年使用:0次
【推荐2】已知双曲线 :
: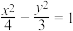 的左、右焦点为
的左、右焦点为 、
、 ,直线
,直线 与双曲线
与双曲线 交于
交于 ,
, 两点.
两点.
(1)已知 过
过 且垂直于
且垂直于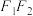 ,求
,求 ;
;
(2)已知直线 的斜率为
的斜率为 ,且直线
,且直线 不过点
不过点 ,设直线
,设直线 、
、 的斜率分别为
的斜率分别为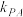 、
、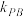 ,求
,求 的值;
的值;
(3)当直线 过
过 时,直线
时,直线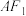 交
交 轴于
轴于 ,直线
,直线 交
交 轴于
轴于 .是否存在直线
.是否存在直线 ,使得
,使得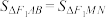 ,若存在,求出直线
,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 :
: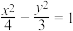 的左、右焦点为
的左、右焦点为 、
、 ,直线
,直线 与双曲线
与双曲线 交于
交于 ,
, 两点.
两点.(1)已知
 过
过 且垂直于
且垂直于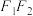 ,求
,求 ;
;(2)已知直线
 的斜率为
的斜率为 ,且直线
,且直线 不过点
不过点 ,设直线
,设直线 、
、 的斜率分别为
的斜率分别为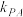 、
、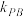 ,求
,求 的值;
的值;(3)当直线
 过
过 时,直线
时,直线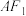 交
交 轴于
轴于 ,直线
,直线 交
交 轴于
轴于 .是否存在直线
.是否存在直线 ,使得
,使得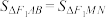 ,若存在,求出直线
,若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
您最近一年使用:0次

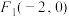 ,
,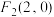 为双曲线E:
为双曲线E: (
( ,
, )的左右焦点,点
)的左右焦点,点 在双曲线E上,O为坐标原点.
在双曲线E上,O为坐标原点.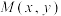 与定点
与定点 的距离和它到定直线l:
的距离和它到定直线l: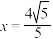 的距离的比是
的距离的比是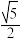 ,记动点M的轨迹为曲线C.
,记动点M的轨迹为曲线C. 的直线l与曲线C交于M,N两点,在x轴上是否存在点Q、使得
的直线l与曲线C交于M,N两点,在x轴上是否存在点Q、使得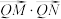 为定值?若存在,求出Q点的坐标及定值;若不存在,请说明理由.
为定值?若存在,求出Q点的坐标及定值;若不存在,请说明理由.


