名校
解题方法
1 . 为营造浓厚的全国文明城市创建氛围,积极响应创建全国文明城市号召,提高对创城行动的责任感和参与度,学校号召师生利用周末参与创城志愿活动.高二(1)班某小组有男生4人,女生2人,现从中随机选取2人作为志愿者参加活动.
(1)求在有女生参加活动的条件下,恰有一名女生参加活动的概率;
(2)记参加活动的女生人数为 ,求
,求 的分布列及期望
的分布列及期望 ;
;
(1)求在有女生参加活动的条件下,恰有一名女生参加活动的概率;
(2)记参加活动的女生人数为
 ,求
,求 的分布列及期望
的分布列及期望 ;
;
您最近半年使用:0次
2 . 某素质训练营设计了一项闯关比赛.规定:三人组队参赛,每次只派一个人,且每人只派一次:如果一个人闯关失败,再派下一个人重新闯关;三人中只要有人闯关成功即视作比赛胜利,无需继续闯关.现有甲、乙、丙三人组队参赛,他们各自闯关成功的概率分别为 、
、 、
、 ,假定
,假定 、
、 、
、 互不相等,且每人能否闯关成功的事件相互独立.
互不相等,且每人能否闯关成功的事件相互独立.
(1)计划依次派甲乙丙进行闯关,若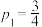 ,
,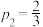 ,
,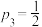 ,求该小组比赛胜利的概率;
,求该小组比赛胜利的概率;
(2)若依次派甲乙丙进行闯关,则写出所需派出的人员数目 的分布,并求
的分布,并求 的期望
的期望 ;
;
(3)已知 ,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
 、
、 、
、 ,假定
,假定 、
、 、
、 互不相等,且每人能否闯关成功的事件相互独立.
互不相等,且每人能否闯关成功的事件相互独立.(1)计划依次派甲乙丙进行闯关,若
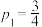 ,
,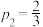 ,
,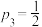 ,求该小组比赛胜利的概率;
,求该小组比赛胜利的概率;(2)若依次派甲乙丙进行闯关,则写出所需派出的人员数目
 的分布,并求
的分布,并求 的期望
的期望 ;
;(3)已知
 ,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
,若乙只能安排在第二个派出,要使派出人员数目的期望较小,试确定甲、丙谁先派出.
您最近半年使用:0次
名校
解题方法
3 . 某老师在课堂测验上设置了五道相互独立的判断题,得分规则是:五道判断题中,全部判断正确得5分,有一道判断错误得3分,有两道判断错误得1分,有三道及以上判断错误得0分.假定随机判断时,每道题判断正确和判断错误的概率均为 .
.
(1)若考生甲所有题目都随机判断,求此考生得分的分布列;
(2)若考生乙能够正确判断其中两道题目,其余题目随机判断,求此考生得分的数学期望.
 .
.(1)若考生甲所有题目都随机判断,求此考生得分的分布列;
(2)若考生乙能够正确判断其中两道题目,其余题目随机判断,求此考生得分的数学期望.
您最近半年使用:0次
解题方法
4 . 据统计,2024年元旦假期,哈尔滨市累计接待游客304.79万人次,实现旅游总收入59.14亿元,游客接待量与旅游总收入达到历史峰值.现对某一时间段冰雪大世界的部分游客做问卷调查,其中75%的游客计划只游览冰雪大世界,另外25%的游客计划既游览冰雪大世界又参观群力音乐公园大雪人.每位游客若只游览冰雪大世界,则得到1份文旅纪念品;若既游览冰雪大世界又参观群力音乐公园大雪人,则获得2份文旅纪念品.假设每位来冰雪大世界景区游览的游客与是否参观群力音乐公园大雪人是相互独立的,用频率估计概率.
(1)从冰雪大世界的游客中随机抽取3人,记这3人获得文旅纪念品的总个数为X,求X的分布列及数学期望;
(2)记 个游客得到文旅纪念品的总个数恰为
个游客得到文旅纪念品的总个数恰为 个的概率为
个的概率为 ,求
,求 的前
的前 项和
项和 .
.
(1)从冰雪大世界的游客中随机抽取3人,记这3人获得文旅纪念品的总个数为X,求X的分布列及数学期望;
(2)记
 个游客得到文旅纪念品的总个数恰为
个游客得到文旅纪念品的总个数恰为 个的概率为
个的概率为 ,求
,求 的前
的前 项和
项和 .
.
您最近半年使用:0次
解题方法
5 . 赣南脐橙,果大形正,橙红鲜绝,光洁美观,已被列为全国十一大优势农产品之一,是江西省赣州市特产,中国国家地理标志产品.荣获“中华名果”等称号.有甲、乙两个脐橙种植基地,按果径 (单位:
(单位: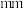 )的大小分级,其中
)的大小分级,其中 为特级果,
为特级果,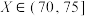 为一级果,
为一级果,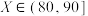 为二级果,
为二级果, 为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:
为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:
(1)根据以上统计数据完成下表,并回答是否有 以上的把握认为“脐橙果径与所在基地有关?”
以上的把握认为“脐橙果径与所在基地有关?”
(2)以样本估计总体,用频率代替概率,从甲种植基地采摘的所有优质果中随机抽取3个,设被抽取的3个脐橙中特级果的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
附: ,
, .
.
 (单位:
(单位: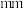 )的大小分级,其中
)的大小分级,其中 为特级果,
为特级果,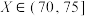 为一级果,
为一级果,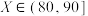 为二级果,
为二级果, 为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:
为三级果,一级果与特级果统称为优质果,现从甲、乙两基地所采摘的所有脐橙中各随机抽取300个,测量这些脐橙的果径,所得数据整理如下:果径分组(单位: |
|
|
|
|
|
|
甲基地频数 | 5 | 15 | 100 | 150 | 25 | 5 |
乙基地频数 | 10 | 25 | 110 | 120 | 25 | 10 |
 以上的把握认为“脐橙果径与所在基地有关?”
以上的把握认为“脐橙果径与所在基地有关?”甲基地 | 乙基地 | |
优质果 | ||
非优质果 |
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
 ,
, .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近半年使用:0次
解题方法
6 . 设离散型随机变量X的分布列为
(1)求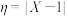 的分布列;
的分布列;
(2)求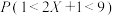 .
.
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.1 | 0.1 | 0.3 | m |
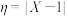 的分布列;
的分布列;(2)求
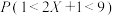 .
.
您最近半年使用:0次
2024高二下·全国·专题练习
7 . 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如表所示.从这200名学生中任意选取1人,求所选同学分数X的分布列,以及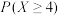 .
.
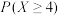 .
.| 等级 | 不及格 | 及格 | 中等 | 良 | 优 |
| 分数 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 20 | 50 | 60 | 40 | 30 |
您最近半年使用:0次
2024高二下·全国·专题练习
解题方法
8 . 某单位为丰富员工的业余生活,利用周末开展趣味野外拉练,此次拉练共分A,B,C三大类,其中A类有3个项目,每项需花费2小时,B类有3个项目,每项需花费3小时,C类有2个项目,每项需花费1小时.要求每位员工从中随机选择3个项目,每个项目的选择机会均等.
(1)求小张在三类中各选1个项目的概率;
(2)设小张所选3个项目花费的总时间为X小时,求X的分布列.
(1)求小张在三类中各选1个项目的概率;
(2)设小张所选3个项目花费的总时间为X小时,求X的分布列.
您最近半年使用:0次
解题方法
9 . 某学校准备订做新的校服,有正装和运动装两种风格可供选择,为了解学生和家长们的偏好,学校随机调查了200名学生及每名学生的一位家长,得到以下的 列联表:
列联表:
(1)根据以上数据,判断是否有 的把握认为学生与家长对校服风格的偏好有差异;
的把握认为学生与家长对校服风格的偏好有差异;
(2)若从家长中按不同偏好的人数比例用分层随机抽样的方法抽取5人进行座谈,再从这5人中任选2人,记这2人中更喜欢正装的家长人数为X,求X的分布列和数学期望.
附: .
.
 列联表:
列联表:更喜欢正装 | 更喜欢运动装 | |
家长 | 120 | 80 |
学生 | 160 | 40 |
 的把握认为学生与家长对校服风格的偏好有差异;
的把握认为学生与家长对校服风格的偏好有差异;(2)若从家长中按不同偏好的人数比例用分层随机抽样的方法抽取5人进行座谈,再从这5人中任选2人,记这2人中更喜欢正装的家长人数为X,求X的分布列和数学期望.
附:
 .
.
| 0.1 | 0.05 | 0.01 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
名校
解题方法
10 . 随机抽取某厂的某种产品 件,经质检,其中有一等品
件,经质检,其中有一等品 件、二等品
件、二等品 件、三等品
件、三等品 件、次品
件、次品 件,已知生产
件,已知生产 件一、二、三等品获得的利润分别为
件一、二、三等品获得的利润分别为 万元、
万元、 万元、
万元、 万元,而
万元,而 件次品亏损
件次品亏损 万元,设
万元,设 件产品的利润
件产品的利润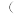 单位:万元
单位:万元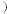 为
为 .
.
(1)求 的分布列;
的分布列;
(2)求 件产品的平均利润
件产品的平均利润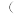 即
即 的数学期望
的数学期望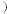 .
.
 件,经质检,其中有一等品
件,经质检,其中有一等品 件、二等品
件、二等品 件、三等品
件、三等品 件、次品
件、次品 件,已知生产
件,已知生产 件一、二、三等品获得的利润分别为
件一、二、三等品获得的利润分别为 万元、
万元、 万元、
万元、 万元,而
万元,而 件次品亏损
件次品亏损 万元,设
万元,设 件产品的利润
件产品的利润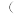 单位:万元
单位:万元 为
为 .
.(1)求
 的分布列;
的分布列;(2)求
 件产品的平均利润
件产品的平均利润 即
即 的数学期望
的数学期望 .
.
您最近半年使用:0次