2023高三·全国·专题练习
1 . 设数列 满足
满足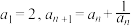 (
(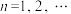 ).证明:
).证明:  对一切正整数n都成立
对一切正整数n都成立
 满足
满足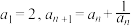 (
(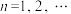 ).证明:
).证明:  对一切正整数n都成立
对一切正整数n都成立
您最近一年使用:0次
2023高三·全国·专题练习
2 . 已知数列 的首项
的首项 ,且
,且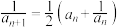 ,
, ,证明:
,证明: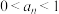 .
.
 的首项
的首项 ,且
,且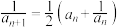 ,
, ,证明:
,证明: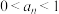 .
.
您最近一年使用:0次
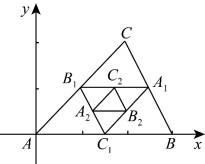
3 . 如图,连接△ABC的各边中点得到一个新的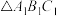 ,又连接
,又连接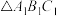 的各边中点得到
的各边中点得到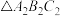 ,如此无限继续下去,得到一系列三角形:
,如此无限继续下去,得到一系列三角形: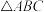 ,
,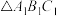 ,
,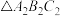 ,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是
,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是______ .
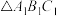 ,又连接
,又连接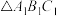 的各边中点得到
的各边中点得到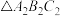 ,如此无限继续下去,得到一系列三角形:
,如此无限继续下去,得到一系列三角形: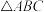 ,
,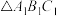 ,
,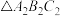 ,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是
,…,这一系列三角形趋向于一个点M.已知A(0,0),B(3,0),C(2,2),则点M的坐标是
您最近一年使用:0次
2022-10-23更新
|
118次组卷
|
2卷引用:2006年普通高等学校招生考试数学(理)试题(福建卷)
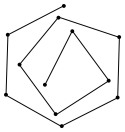
4 . 如图,画一个正三角形,不画第三边;接着画正方形,对这个正方形,不画第四边,接着画正五边形;对这个正五边形不画第五边,接着画正六边形;……,这样无限画下去,形成一条无穷伸展的等边折线.设第n条线段与第 条线段所夹的角为
条线段所夹的角为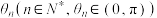 ,则
,则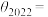
______ .
 条线段所夹的角为
条线段所夹的角为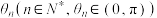 ,则
,则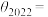
您最近一年使用:0次
2022-04-28更新
|
901次组卷
|
5卷引用:上海市上海交通大学附属中学2022届高三下学期期中数学试题
上海市上海交通大学附属中学2022届高三下学期期中数学试题(已下线)文科数学-2022年高考考前20天终极冲刺攻略(二)(已下线)专题14数学知识的延伸必考题型分类训练-2福建省永春一中、培元中学、石光中学、季延中学2024届高三下学期第二次联合考试数学试题云南省昆明市第三中学2023-2024学年高二下学期第二次综合测试(4月)数学试题
5 . 给定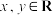 .若
.若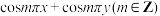 共取有限个不同值,证明:x,
共取有限个不同值,证明:x, .
.
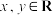 .若
.若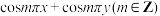 共取有限个不同值,证明:x,
共取有限个不同值,证明:x, .
.
您最近一年使用:0次
6 . 魏晋时期数学家刘徽首创割圆术,他在《九章算术》方田章圆田术中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”注述中所用的割圆术是一种无限与有限的转化过程,比如在正数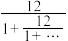 中的“
中的“ ”代表无限次重复,设
”代表无限次重复,设 ,则可以利用方程
,则可以利用方程 求得
求得 ,类似地可得到正数
,类似地可得到正数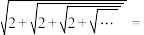 ( )
( )
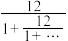 中的“
中的“ ”代表无限次重复,设
”代表无限次重复,设 ,则可以利用方程
,则可以利用方程 求得
求得 ,类似地可得到正数
,类似地可得到正数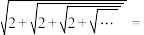 ( )
( )| A.2 | B.3 | C. | D.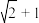 |
您最近一年使用:0次
2021-02-06更新
|
951次组卷
|
12卷引用:江西省江西师范大学附属中学2020-2021学年高二上学期期末考试数学(文)试题
江西省江西师范大学附属中学2020-2021学年高二上学期期末考试数学(文)试题江西省江西师范大学附属中学2020-2021学年高二上学期期末考试数学(理)试题(已下线)2.1.1 合情推理(基础练)-2020-2021学年高二数学(理)十分钟同步课堂专练(人教A版选修2-2)江西省吉安市永丰县永丰中学2020-2021学年高二下学期期中考试数学(文)试题江西省宜春市奉新县第一中学2020-2021学年高二下学期第二次月考数学(理)试题陕西省咸阳市实验中学2020-2021学年高二下学期第一次月考理科数学试题陕西省宝鸡市金台区2020-2021学年高二下学期期中文科数学试题(已下线)2.1.1 合情推理(基础练)-2020-2021学年高二数学(文)十分钟同步课堂专练(人教A版选修1-2)江西省师范大学附属中学2021-2022学年高二上学期期末数学(理)试题江西省师范大学附属中学2021-2022学年高二上学期期末数学(文)试题广西北流市高级中学2021-2022学年高二3月月考数学(文)试题陕西省渭南市华州区咸林中学2021-2022学年高二下学期期中文科数学试题
7 . 魏晋时期数学家刘徽首创割圆术,他在注释《九章算术》中指出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”这是一种无限与有限的转化过程,比如在正数 中的“…”代表无限次重复,设
中的“…”代表无限次重复,设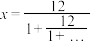 ,则可以利用方程
,则可以利用方程 得
得 ,类似地可得到正数
,类似地可得到正数
________ .
 中的“…”代表无限次重复,设
中的“…”代表无限次重复,设 ,则可以利用方程
,则可以利用方程 得
得 ,类似地可得到正数
,类似地可得到正数
您最近一年使用:0次
2020-07-23更新
|
105次组卷
|
3卷引用:陕西省西安市莲湖区2019-2020学年高二下学期期末考试数学(文)试题
8 . 我国古代数学名著《九章算术注》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式 中“
中“ ”即代表无数次重复,但原式却是个定值,它可以通过方程
”即代表无数次重复,但原式却是个定值,它可以通过方程 求得
求得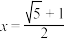 .类比上述过程,则
.类比上述过程,则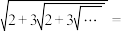
________ .
 中“
中“ ”即代表无数次重复,但原式却是个定值,它可以通过方程
”即代表无数次重复,但原式却是个定值,它可以通过方程 求得
求得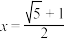 .类比上述过程,则
.类比上述过程,则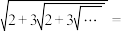
您最近一年使用:0次
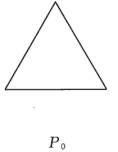
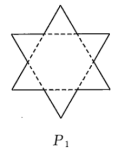
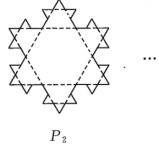
9 . 如图所示,有一列曲线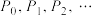 .已知
.已知 所围成的图形是面积为1的等边三角形,
所围成的图形是面积为1的等边三角形, 是对
是对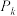 进行如下操作:将
进行如下操作:将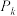 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(
的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(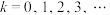 ).记
).记 为曲线
为曲线 所围成图形的面积.
所围成图形的面积.
(1)求数列 的通项公式;
的通项公式;
(2)求 .
.
 .已知
.已知 所围成的图形是面积为1的等边三角形,
所围成的图形是面积为1的等边三角形, 是对
是对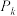 进行如下操作:将
进行如下操作:将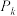 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(
的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉(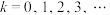 ).记
).记 为曲线
为曲线 所围成图形的面积.
所围成图形的面积.


(1)求数列
 的通项公式;
的通项公式;(2)求
 .
.
您最近一年使用:0次
10 . 在平面直角坐标系中,函数 在第一象限内的图像如图所示,试做如下操作,把
在第一象限内的图像如图所示,试做如下操作,把 轴上的区间
轴上的区间 等分成
等分成 个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数 的图像上.若用
的图像上.若用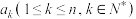 ,表示第
,表示第 个矩形的面积,
个矩形的面积, 表示这
表示这 个矩形的面积总和.
个矩形的面积总和.

(Ⅰ)求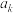 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明等式: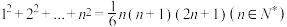 ;
;
(Ⅲ)求 的值,并说明
的值,并说明 的几何意义.
的几何意义.
 在第一象限内的图像如图所示,试做如下操作,把
在第一象限内的图像如图所示,试做如下操作,把 轴上的区间
轴上的区间 等分成
等分成 个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数
个小区间,在每一个小区间上作一个小矩形,使矩形的右端点落在函数 的图像上.若用
的图像上.若用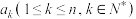 ,表示第
,表示第 个矩形的面积,
个矩形的面积, 表示这
表示这 个矩形的面积总和.
个矩形的面积总和.
(Ⅰ)求
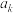 的表达式;
的表达式;(Ⅱ)请用数学归纳法证明等式:
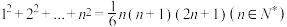 ;
;(Ⅲ)求
 的值,并说明
的值,并说明 的几何意义.
的几何意义.
您最近一年使用:0次
2020-06-03更新
|
285次组卷
|
4卷引用:上海市青浦区2019-2020学年高二上学期期中数学试题



