名校
1 . 设平面内两个非零向量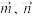 的夹角为
的夹角为 ,定义一种运算“
,定义一种运算“ ”:
”: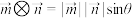 .试求解下列问题,
.试求解下列问题,
(1)已知向量 满足
满足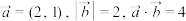 ,求
,求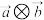 的值;
的值;
(2)在平面直角坐标系中,已知点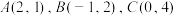 ,求
,求 的值;
的值;
(3)已知向量 ,求
,求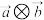 的最小值.
的最小值.
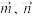 的夹角为
的夹角为 ,定义一种运算“
,定义一种运算“ ”:
”: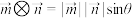 .试求解下列问题,
.试求解下列问题,(1)已知向量
 满足
满足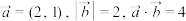 ,求
,求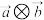 的值;
的值;(2)在平面直角坐标系中,已知点
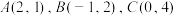 ,求
,求 的值;
的值;(3)已知向量
 ,求
,求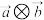 的最小值.
的最小值.
您最近一年使用:0次
2024-04-10更新
|
916次组卷
|
4卷引用:江苏省启东中学2023-2024学年高一下学期期中考试数学试题
2023高三·全国·专题练习
解题方法
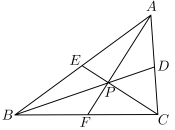
2 . 请你根据“奔驰定理”对以下命题进行判断:
①若P是 的重心,则有
的重心,则有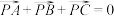 ;
;
②若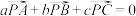 成立,则P是
成立,则P是 的内心;
的内心;
③若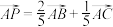 ,则
,则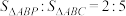 ;
;
④若P是 的外心,
的外心, ,
,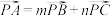 ,则
,则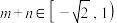 ;
;
⑤若 的内角A,B,C的对边分别为a,b,c,且
的内角A,B,C的对边分别为a,b,c,且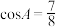 ,O为
,O为 内的一点且为内心.若
内的一点且为内心.若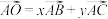 ,则
,则 的最大值为
的最大值为 .
.
则正确的命题有________ .(填序号)
①若P是
 的重心,则有
的重心,则有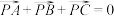 ;
;②若
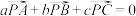 成立,则P是
成立,则P是 的内心;
的内心;③若
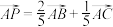 ,则
,则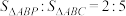 ;
;④若P是
 的外心,
的外心, ,
,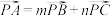 ,则
,则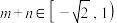 ;
;⑤若
 的内角A,B,C的对边分别为a,b,c,且
的内角A,B,C的对边分别为a,b,c,且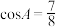 ,O为
,O为 内的一点且为内心.若
内的一点且为内心.若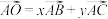 ,则
,则 的最大值为
的最大值为 .
.则正确的命题有

您最近一年使用:0次
解题方法
3 . 我们把由平面内夹角成 的两条数轴
的两条数轴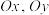 构成的坐标系,称为“@未来坐标系”.如图所示,
构成的坐标系,称为“@未来坐标系”.如图所示,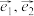 分别为
分别为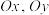 正方向上的单位向量.若向量
正方向上的单位向量.若向量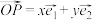 ,则把实数对
,则把实数对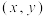 叫做向量
叫做向量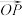 的“@未来坐标”,记
的“@未来坐标”,记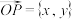 .已知
.已知 分别为向是
分别为向是 的@未来坐标.
的@未来坐标. ;
;
(2)若向量 的“@未来坐标”分别为
的“@未来坐标”分别为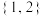 ,
,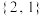 ,求向量
,求向量 的夹角的余弦值.
的夹角的余弦值.
 的两条数轴
的两条数轴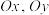 构成的坐标系,称为“@未来坐标系”.如图所示,
构成的坐标系,称为“@未来坐标系”.如图所示,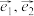 分别为
分别为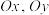 正方向上的单位向量.若向量
正方向上的单位向量.若向量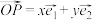 ,则把实数对
,则把实数对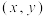 叫做向量
叫做向量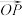 的“@未来坐标”,记
的“@未来坐标”,记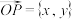 .已知
.已知 分别为向是
分别为向是 的@未来坐标.
的@未来坐标.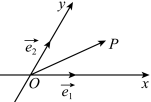
 ;
;(2)若向量
 的“@未来坐标”分别为
的“@未来坐标”分别为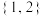 ,
,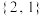 ,求向量
,求向量 的夹角的余弦值.
的夹角的余弦值.
您最近一年使用:0次
2023-06-23更新
|
725次组卷
|
11卷引用:模块一专题3 《平面向量的应用》A基础卷(苏教版)
(已下线)模块一专题3 《平面向量的应用》A基础卷(苏教版)(已下线)模块三 专题2 解答题分类练 专题1 平面向量运算(解答题)(苏教版)浙江省杭州市2022-2023学年高一下学期期末数学试题(已下线)模块一 专题3 平面向量的应用(A)(已下线)模块三 专题2 专题1 平面向量运算(已下线)模块三 专题2 解答题分类练 专题3 平面向量各类运算(解答题)(已下线)模块三专题4大题分类练(专题3 平面向量数量积)【高一下人教B版】(已下线)重组4 高一期末真题重组卷(浙江卷)B提升卷(已下线)模块四 专题2 高考新题型专练(新定义专练)(人教A)(已下线)模块三 专题3 高考新题型专练(新定义专练)(苏教版)(已下线)模块三 专题3 高考新题型专练(新定义专练)(北师大2019版)
名校
4 . 在平面直角坐标系中, 为坐标原点,对任意两个向量
为坐标原点,对任意两个向量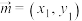 ,
,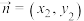 ,作
,作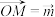 ,
, .当
.当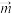 ,
,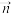 不共线时,记以
不共线时,记以 ,
, 为邻边的平行四边形的面积为
为邻边的平行四边形的面积为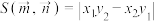 ;当
;当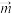 ,
,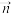 共线时,规定
共线时,规定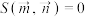 .
.
(1)分别根据下列已知条件求 :
:
①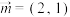 ,
, ;②
;②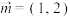 ,
,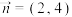 ;
;
(2)若向量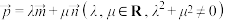 ,求证:
,求证: ;
;
(3)若A,B,C是以О为圆心的单位圆上不同的点,记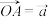 ,
,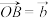 ,
,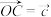 .
.
(i)当 时,求
时,求 的最大值;
的最大值;
(ii)写出 的最大值.(只需写出结果)
的最大值.(只需写出结果)
 为坐标原点,对任意两个向量
为坐标原点,对任意两个向量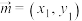 ,
,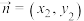 ,作
,作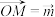 ,
, .当
.当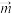 ,
,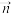 不共线时,记以
不共线时,记以 ,
, 为邻边的平行四边形的面积为
为邻边的平行四边形的面积为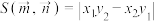 ;当
;当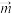 ,
,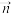 共线时,规定
共线时,规定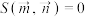 .
.(1)分别根据下列已知条件求
 :
:①
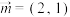 ,
, ;②
;②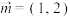 ,
,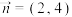 ;
;(2)若向量
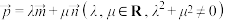 ,求证:
,求证: ;
;(3)若A,B,C是以О为圆心的单位圆上不同的点,记
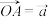 ,
,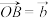 ,
,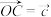 .
.(i)当
 时,求
时,求 的最大值;
的最大值;(ii)写出
 的最大值.(只需写出结果)
的最大值.(只需写出结果)
您最近一年使用:0次
2022-07-08更新
|
1256次组卷
|
15卷引用:江苏省苏州市昆山中学2023-2024学年高一下学期3月月考数学试题
江苏省苏州市昆山中学2023-2024学年高一下学期3月月考数学试题江苏省连云港高级中学2023-2024学年高一下学期期中考试数学试卷(已下线)作业01 平面向量及其应用-【暑假分层作业】(苏教版2019必修第二册)北京市丰台区2021-2022学年高一下学期期末练习数学试题北京工业大学附属中学2022-2023学年高一下学期期末数学综合练习试题(二 )广东省广东实验中学深圳学校2022-2023学年高一下学期期中数学试题(已下线)重难点01平面向量的实际应用与新定义(3)北京市清华大学附属中学朝阳学校2023-2024学年高一下学期3月月考数学试卷吉林省东北师范大学附属中学2023-2024学年高一下学期阶段验收考试数学试题河南省三门峡市卢氏县第一高级中学2023-2024学年高一下学期期中数学试题(已下线)模块四 期中重组卷4(江苏苏北五市)(苏教版)【北京专用】专题07平面向量(第三部分)-高一下学期名校期末好题汇编北京市东直门中学2023-2024学年高一下学期期中考试数学试题宁夏银川市2023-2024学年高一下学期期中考试数学试卷(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大题型)(练习)
名校
解题方法
5 . 在平面直角坐标系 内,设两个向量
内,设两个向量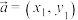 ,
,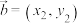 ,定义运算:
,定义运算: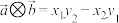 ,下列说法正确的是( )
,下列说法正确的是( )
 内,设两个向量
内,设两个向量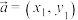 ,
,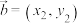 ,定义运算:
,定义运算: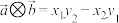 ,下列说法正确的是( )
,下列说法正确的是( )A.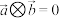 是 是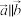 的充要条件 的充要条件 | B. |
C. | D.若点 , , , , 不共线,则 不共线,则 的面积 的面积 |
您最近一年使用:0次
名校
6 . 引入平面向量之间的一种新运算“ ”如下:对任意的向量
”如下:对任意的向量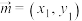 ,
,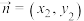 ,规定
,规定 ,则对于任意的向量
,则对于任意的向量 ,
, ,
,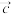 ,下列说法正确的有( )
,下列说法正确的有( )
 ”如下:对任意的向量
”如下:对任意的向量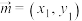 ,
,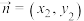 ,规定
,规定 ,则对于任意的向量
,则对于任意的向量 ,
, ,
,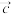 ,下列说法正确的有( )
,下列说法正确的有( )A. | B. |
C. | D. |
您最近一年使用:0次
2021-01-14更新
|
1546次组卷
|
13卷引用:江苏省新区实验2020-2021学年高一下学期期中数学试题
江苏省新区实验2020-2021学年高一下学期期中数学试题江苏省苏州市实验中学2020-2021学年高一下学期期中数学试题江苏省南通市通州区金沙中学2021-2022学年高一下学期3月学业水平质量调研数学试题江苏省泰州市2020-2021学年高三上学期期末数学试题江苏省南京师范大学《数学之友》2021届高三下学期二模数学试题湖南省长沙市明达中学2020-2021学年高一下学期3月月考数学试题苏教版(2019) 必修第二册 必杀技 专练1 新定义、新情境专练安徽省滁州市定远县第三中学2022-2023学年高一下学期2月月考数学试题黑龙江省双鸭山市第一中学2023-2024学年高一下学期4月月考数学试题江西省南昌市第五高级中学2023-2024学年高一下学期期中考试数学试卷【巩固卷】 专练1 新定义、新情境专练单元测试A-湘教版(2019)必修(第二册)(已下线)专题06 平面向量(测)-2021年高考数学二轮复习讲练测(新高考版)(已下线)解密07 平面向量(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)
7 . 小顾同学在用向量法研究解三角形面积问题时有如下研究成果:若 ,
,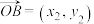 ,则
,则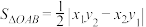 .试用上述成果解决问题:已知
.试用上述成果解决问题:已知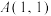 ,
,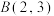 ,
,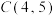 ,则
,则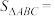
___________ .
 ,
,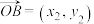 ,则
,则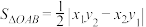 .试用上述成果解决问题:已知
.试用上述成果解决问题:已知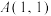 ,
,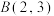 ,
,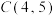 ,则
,则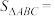
您最近一年使用:0次
2022-05-05更新
|
545次组卷
|
4卷引用:江苏省南通市海安市曲塘中学2021-2022学年高一下学期期中数学试题
江苏省南通市海安市曲塘中学2021-2022学年高一下学期期中数学试题河北省衡水市武强中学2022-2023学年高一下学期3月调研数学试题浙江省绍兴市越州中学2022-2023学年高一下学期期中数学试题(已下线)模块三 专题3 高考新题型专练(新定义专练)(苏教版)
8 . 我们可以把平面向量坐标的概念推广为“复向量”,即可将有序复数对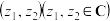 视为一个向量,记作
视为一个向量,记作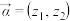 .两个复向量
.两个复向量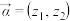 ,
,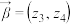 的线性运算定义为:
的线性运算定义为: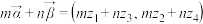 ,
,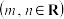 ;两个复向量
;两个复向量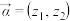 ,
,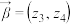 的积记作
的积记作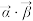 ,定义为
,定义为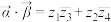 ;复向量
;复向量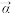 的模定义为
的模定义为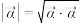 ;若复向量
;若复向量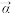 与
与 满足
满足 ,则称复向量
,则称复向量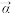 与
与 平行.
平行.
(1)设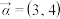 ,
,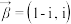 ,求
,求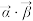 以及
以及 ;
;
(2)对于实数 ,判断
,判断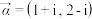 与
与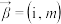 能否平行,若能求出
能否平行,若能求出 的值,若不能,说明理由;
的值,若不能,说明理由;
(3)设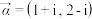 ,
,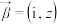 ,
,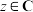 ,且复向量
,且复向量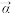 与
与 平行,求复数
平行,求复数 .
.
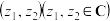 视为一个向量,记作
视为一个向量,记作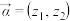 .两个复向量
.两个复向量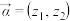 ,
,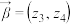 的线性运算定义为:
的线性运算定义为: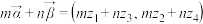 ,
,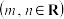 ;两个复向量
;两个复向量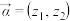 ,
,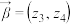 的积记作
的积记作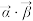 ,定义为
,定义为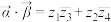 ;复向量
;复向量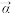 的模定义为
的模定义为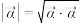 ;若复向量
;若复向量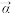 与
与 满足
满足 ,则称复向量
,则称复向量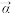 与
与 平行.
平行.(1)设
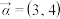 ,
,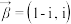 ,求
,求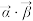 以及
以及 ;
;(2)对于实数
 ,判断
,判断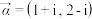 与
与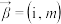 能否平行,若能求出
能否平行,若能求出 的值,若不能,说明理由;
的值,若不能,说明理由;(3)设
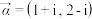 ,
,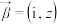 ,
,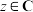 ,且复向量
,且复向量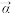 与
与 平行,求复数
平行,求复数 .
.
您最近一年使用:0次
9 . 定义平面向量之间的一种运算“ ”如下,对任意的
”如下,对任意的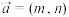 ,
,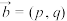 ,令
,令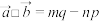 ,下面说法错误的是( )
,下面说法错误的是( )
 ”如下,对任意的
”如下,对任意的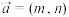 ,
,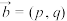 ,令
,令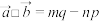 ,下面说法错误的是( )
,下面说法错误的是( )A.若 与 与 共线,则 共线,则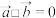 | B. |
C.对任意的 ,有 ,有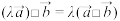 | D. |
您最近一年使用:0次
2019-01-30更新
|
1176次组卷
|
34卷引用:江苏省苏州中学2020-2021学年高一下学期3月月考数学试题
江苏省苏州中学2020-2021学年高一下学期3月月考数学试题江苏省南京市第二十九中学2020-2021学年高一下学期3月月考数学试题江苏省扬州市仪征中学2020-2021学年高一下学期4月学情检测数学试题(已下线)2010-2011学年辽宁省辽南协作体高一下学期期中考试数学(理)(已下线)2011-2012学年四川省资阳中学高一下学期期中理科数学试卷2015-2016学年广东省普宁市华侨中学高一上学期第一次月考数学试卷广西南宁市第八中学2017-2018学年高一下学期期末考试数学试题辽宁抚顺十中2019-2020学年高一下学期新教材线上检测数学试题山东省济宁市兖州区2019-2020学年高一下学期5月阶段性测试数学试题广东省佛山市第一中学2019-2020学年高一下学期期中数学试题(已下线)【新东方】双师170高一下黑龙江省齐齐哈尔市第八中学校2020-2021学年高一下学期期中数学试题沪教版(2020) 必修第二册 新课改一课一练 第8章 8.3.4向量数量积与夹角的坐标表示福建省南平市浦城县2022-2023学年高一下学期3月月考数学试题【课堂练】 8.3.4 向量数量积与夹角的坐标表示 随堂练习-沪教版(2020)必修第二册 第8章 平面向量2010年普通高等学校招生全国统一考试山东卷理科数学(已下线)2010年高考试题分项版理科数学之专题五 平面向量2010年普通高等学校招生全国统一考试(山东卷)文科数学全解全析(已下线)2012届广东省惠州市高三第四次调研(一模)文科数学试卷(已下线)2013届山东省高三高考压轴理科数学试卷(已下线)2013届江西省高考压轴理科数学试卷(已下线)2013届山东省高三高考压轴文科数学试卷2017年北京市牛栏山一中高三文十月月试题山东省日照市五莲县2019-2020学年高三上学期模块诊断性检测数学试题2020届浙江省杭州市建人高复高三下学期4月模拟测试数学试题(已下线)题型04 平面向量数量积与三角形平面向量中线定理-2020届秒杀高考数学题型之平面向量(已下线)第11练 平面向量的数量积-2021年高考数学一轮复习小题必刷(山东专用)浙江省杭州市建人高复学校2020届高三下学期5月模拟数学试题(已下线)专题3.3 平面向量-备战2021年高考数学精选考点专项突破题集(新高考地区)内蒙古乌海市第一中学2021-2022学年高三上学期第一次月考文科数学试题人教B版(2019) 必修第三册 学习帮手 第八章 检测(已下线)解密07 平面向量(讲义)-【高频考点解密】2022年高考数学二轮复习讲义+分层训练(浙江专用)(已下线)第10讲:第五章 平面向量及解三角形(测)(基础拿分卷)(已下线)第一篇 代数与近世代数 专题2 群、环、域等新定义问题 微点1 群、环、域等新定义问题
15-16高二上·上海浦东新·期中
名校
10 . 对于向量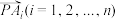 ,把能够使得
,把能够使得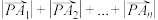 取到最小值的点
取到最小值的点 称为
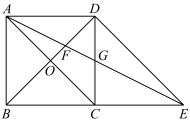
称为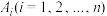 的“平衡点”.如图,矩形
的“平衡点”.如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,延长
,延长 至
至 ,使得
,使得 ,联结
,联结 ,分别交
,分别交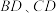 于
于 两点.下列的结论中,正确的是( )
两点.下列的结论中,正确的是( )
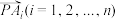 ,把能够使得
,把能够使得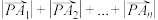 取到最小值的点
取到最小值的点 称为
称为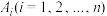 的“平衡点”.如图,矩形
的“平衡点”.如图,矩形 的两条对角线相交于点
的两条对角线相交于点 ,延长
,延长 至
至 ,使得
,使得 ,联结
,联结 ,分别交
,分别交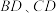 于
于 两点.下列的结论中,正确的是( )
两点.下列的结论中,正确的是( )
A. 的“平衡点”为 的“平衡点”为 . . |
B.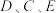 的“平衡点”为 的“平衡点”为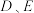 的中点. 的中点. |
C.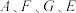 的“平衡点”存在且唯一. 的“平衡点”存在且唯一. |
D.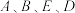 的“平衡点”必为 的“平衡点”必为 |
您最近一年使用:0次
2020-01-10更新
|
700次组卷
|
6卷引用:江苏省无锡市江阴市华士高级中学2023-2024学年高一下学期3月月考数学试卷
江苏省无锡市江阴市华士高级中学2023-2024学年高一下学期3月月考数学试卷重庆市凤鸣山中学2020-2021学年高一下学期期中数学试题(已下线)上海市华东师范大学第二附属中学2015-2016学年高二上学期期中数学试题(已下线)专题17 数学中的新定义问题-2021年高考冲刺之二轮专题精讲精析(已下线)专题8.2 创新型问题 玩转压轴题-玩转压轴题,进军满分之2021高考数学选择题填空题(已下线)【讲】 专题四 与平面向量有关的新定义问题(压轴大全)



