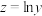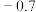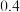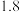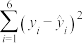1 . “现值”与“终值”是利息计算中的两个基本概念,终值是现在的一笔钱按给定的利息率计算所得到的在未来某个时间点的价值。现值是未来的一笔钱按给定的利息率计算所得到的现在的价值。例如,在复利计息的情况下,设本金为A,每期利率为r,期数为n,到期末的本利和为S,则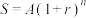 其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为
其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为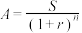 .现有如下问题:小明想买一套房子有如下两个方案
.现有如下问题:小明想买一套房子有如下两个方案
方案一:一次性付全款50万元;
方案二:分期付款,每年初付款6万元,第十年年初付完;
(1)已知一年期存款的年利率为4%,试讨论两种方案哪一种更好?
(2)若小明把房子租出去,第一年年初需交纳租金2万元,此后每年初涨租金1000元,假设存款的年利率为4%,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元).参考数据:
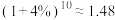 .
.
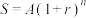 其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为
其中,S称为n期末的终值,A称为n期后终值S的现值,即n期后的S元现在的价值为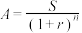 .现有如下问题:小明想买一套房子有如下两个方案
.现有如下问题:小明想买一套房子有如下两个方案方案一:一次性付全款50万元;
方案二:分期付款,每年初付款6万元,第十年年初付完;
(1)已知一年期存款的年利率为4%,试讨论两种方案哪一种更好?
(2)若小明把房子租出去,第一年年初需交纳租金2万元,此后每年初涨租金1000元,假设存款的年利率为4%,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元).参考数据:
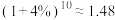 .
.
您最近一年使用:0次
2023-10-29更新
|
355次组卷
|
3卷引用:1.4 数列在日常经济生活中的应用4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)
(已下线)1.4 数列在日常经济生活中的应用4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)河南省郑州市宇华实验学校2024届高三上学期期末数学试题山东省济南市莱芜第一中学2023-2024学年高三上学期10月月考数学试题
2 . 已知 ,
, ,
, ,
, 四名选手参加某项比赛,其中
四名选手参加某项比赛,其中 ,
, 为种子选手,
为种子选手, ,
, 为非种子选手,种子选手对非种子选手种子选手获胜的概率为
为非种子选手,种子选手对非种子选手种子选手获胜的概率为 ,种子选手之间的获胜的概率为
,种子选手之间的获胜的概率为 ,非种子选手之间获胜的概率为
,非种子选手之间获胜的概率为 .比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.
.比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.
(1)若你是主办方,则第一轮选手的对战安排一共有多少不同的方案?
(2)选手 与选手
与选手 相遇的概率为多少?
相遇的概率为多少?
(3)以下两种方案,哪一种种子选手夺冠的概率更大?
方案一:第一轮比赛种子选手与非种子选手比赛;
方案二:第一轮比赛种子选手与种子选手比赛.
 ,
, ,
, ,
, 四名选手参加某项比赛,其中
四名选手参加某项比赛,其中 ,
, 为种子选手,
为种子选手, ,
, 为非种子选手,种子选手对非种子选手种子选手获胜的概率为
为非种子选手,种子选手对非种子选手种子选手获胜的概率为 ,种子选手之间的获胜的概率为
,种子选手之间的获胜的概率为 ,非种子选手之间获胜的概率为
,非种子选手之间获胜的概率为 .比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.
.比赛规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军.(1)若你是主办方,则第一轮选手的对战安排一共有多少不同的方案?
(2)选手
 与选手
与选手 相遇的概率为多少?
相遇的概率为多少?(3)以下两种方案,哪一种种子选手夺冠的概率更大?
方案一:第一轮比赛种子选手与非种子选手比赛;
方案二:第一轮比赛种子选手与种子选手比赛.
您最近一年使用:0次
2024-05-19更新
|
1372次组卷
|
5卷引用:核心考点5 条件概率与全概率公式 B提升卷 (高二期末考试必考的10大核心考点)
(已下线)核心考点5 条件概率与全概率公式 B提升卷 (高二期末考试必考的10大核心考点) 山东中学联盟2024届高考考前热身押题数学试题(已下线)专题5.2 事件的独立及频率与概率-重难点突破及混淆易错规避(人教A版2019必修第二册)(已下线)第十章 本章综合--方法提升应用【第三练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)期末模拟卷(范围:人教A版2019必修第二册)-期末真题分类汇编(天津专用)
3 . “现值”与“终值”是利息计算中的两个基本概念,掌握好这两个概念,对于顺利解决有关金融中的数学问题以及理解各种不同的算法都是十分有益的.所谓“现值”是指在 期末的金额,把它扣除利息后,折合成现时的值,而“终值”是指
期末的金额,把它扣除利息后,折合成现时的值,而“终值”是指 期后的本利和.它们计算的基点分别是存期的起点和终点.例如,在复利计息的情况下,设本金为
期后的本利和.它们计算的基点分别是存期的起点和终点.例如,在复利计息的情况下,设本金为 ,每期利率为
,每期利率为 ,期数为
,期数为 ,到期末的本利和为
,到期末的本利和为 ,则
,则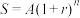 其中,
其中, 称为
称为 期末的终值,
期末的终值, 称为
称为 期后终值
期后终值 的现值,即
的现值,即 期后的
期后的 元现在的价值为
元现在的价值为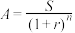 .
.
现有如下问题:小明想买一座公寓有如下两个方案
方案一:一次性付全款25万元;
方案二:分期付款,每年初付款3万元,第十年年初付完;
(1)已知一年期存款的年利率为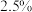 ,试讨论两种方案哪一种更好?
,试讨论两种方案哪一种更好?
(2)若小明把房子租出去,第一年年初需交纳租金2万元,此后每年初涨租金1000元,参照第(1))问中的存款年利率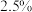 ,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元)
,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元)
参考数据: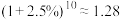
 期末的金额,把它扣除利息后,折合成现时的值,而“终值”是指
期末的金额,把它扣除利息后,折合成现时的值,而“终值”是指 期后的本利和.它们计算的基点分别是存期的起点和终点.例如,在复利计息的情况下,设本金为
期后的本利和.它们计算的基点分别是存期的起点和终点.例如,在复利计息的情况下,设本金为 ,每期利率为
,每期利率为 ,期数为
,期数为 ,到期末的本利和为
,到期末的本利和为 ,则
,则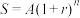 其中,
其中, 称为
称为 期末的终值,
期末的终值, 称为
称为 期后终值
期后终值 的现值,即
的现值,即 期后的
期后的 元现在的价值为
元现在的价值为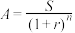 .
.现有如下问题:小明想买一座公寓有如下两个方案
方案一:一次性付全款25万元;
方案二:分期付款,每年初付款3万元,第十年年初付完;
(1)已知一年期存款的年利率为
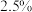 ,试讨论两种方案哪一种更好?
,试讨论两种方案哪一种更好?(2)若小明把房子租出去,第一年年初需交纳租金2万元,此后每年初涨租金1000元,参照第(1))问中的存款年利率
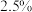 ,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元)
,预计第十年房租到期后小明所获得全部租金的终值.(精确到百元)参考数据:
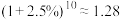
您最近一年使用:0次
2023-03-26更新
|
1559次组卷
|
6卷引用:1.4 数列在日常经济生活中的应用4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)
(已下线)1.4 数列在日常经济生活中的应用4种常见考法归类-【帮课堂】2023-2024学年高二数学同步学与练(北师大版2019选择性必修第二册)(已下线)考点8 等差、等比数列的实际应用 2024届高考数学考点总动员(已下线)重难点10 数列的通项、求和及综合应用【九大题型】湖南省郴州市2023届高三下学期三模数学试题(已下线)专题19 数列应用题的解法 微点2 数列应用题综合训练(已下线)模块四 专题6 大题分类练(数列)拔高能力练(人教A)
名校
解题方法
4 . 新冠疫情不断反弹,各大商超多措并举确保市民生活货品不断档,超市员工加班加点工作.某大型超市为答谢各位员工一年来的锐意进取和辛勤努力,拟在年会后,通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有5种面值奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2023-04-14更新
|
661次组卷
|
9卷引用:第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)
(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题03 条件概率与全概率公式(3)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(5)山东省德州市2022-2023学年高二上学期期末数学试题(已下线)模块一 专题2 概率统计 (人教B)(已下线)模块三 专题5 概率与统计--拔高能力练(人教B版)福建省宁德市寿宁县第一中学2022-2023学年高二下学期第二阶段考试(5月)数学试题江苏省连云港高级中学2022-2023学年高二下学期期中数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)
名校
解题方法
5 . 矮化密植是指应用生物或栽培措施使果树生长树冠紧凑的方法,它与常规的矮小栽培相比有许多优势,如采用这种矮化果树可以建立比常规果园定植密度更高的果园,不仅能提高土壤及光能利用率,还能够获得更多的早期经济效益.某乡镇计划引进A,B两种矮化果树,已知A种矮化果树种植成功率为 ,成功后每公顷收益7.5万元;B种矮化果树种植成功率为
,成功后每公顷收益7.5万元;B种矮化果树种植成功率为 ,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.
,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.
(1)甲种植户试种两种矮化果树各1公顷,总收益为X万元,求X的分布列及数学期望;
(2)乙种植户有良田6公顷,本计划全部种植A,但是甲劝说乙应该种植两种矮化果树各3公顷,请按照总收益的角度分析一下,乙应选择哪一种方案?
 ,成功后每公顷收益7.5万元;B种矮化果树种植成功率为
,成功后每公顷收益7.5万元;B种矮化果树种植成功率为 ,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.
,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.(1)甲种植户试种两种矮化果树各1公顷,总收益为X万元,求X的分布列及数学期望;
(2)乙种植户有良田6公顷,本计划全部种植A,但是甲劝说乙应该种植两种矮化果树各3公顷,请按照总收益的角度分析一下,乙应选择哪一种方案?
您最近一年使用:0次
2024-01-10更新
|
395次组卷
|
5卷引用:第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)
(已下线)第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)江西省南昌市第十九中学2023-2024学年高二上学期期末考试数学试卷(已下线)7.3.1 离散型随机变量的均值——课后作业(巩固版)(已下线)专题3.2离散型随机变量的分布列及数字特征(七个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)2024届河南省名校学术联盟高考模拟信息卷&押题卷数学(三)
6 . 2022年是中国共产主义青年团成立100周年,某中学为此举办了一次共青团史知识竞赛,并规定成绩在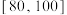 内为成绩优秀.现对参赛的100名学生的竞赛成绩进行统计,得到如下人数分布表.
内为成绩优秀.现对参赛的100名学生的竞赛成绩进行统计,得到如下人数分布表.
(1)根据以上数据完成 列联表,并判断是否有95%的把握认为此次竞赛成绩与该学生是初中生还是高中生有关;
列联表,并判断是否有95%的把握认为此次竞赛成绩与该学生是初中生还是高中生有关;
(2)为鼓励学生积极参加这次知识竞赛,学校后勤部给参与竞赛的学生制定了两种不同的奖励方案:
方案一:参加了竞赛的学生每人都可抽奖1次,且每次抽奖互不影响,每次中奖的概率均为 ,抽中奖励价值50元的食堂充值卡,未抽中无奖励;方案二:竞赛成绩优秀的抽奖两次,其余学生抽奖一次,抽奖者点击抽奖按钮,即随机产生一个数字(
,抽中奖励价值50元的食堂充值卡,未抽中无奖励;方案二:竞赛成绩优秀的抽奖两次,其余学生抽奖一次,抽奖者点击抽奖按钮,即随机产生一个数字(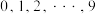 ),若产生的数字能被3整除,则可奖励价值40元的食堂充值卡,否则奖励20元的食堂充值卡(充值卡奖励可叠加).若学校后勤部负责人希望让学生得到更多的奖励,则该负责人应该选择哪一种奖励方案,并说明理由.
),若产生的数字能被3整除,则可奖励价值40元的食堂充值卡,否则奖励20元的食堂充值卡(充值卡奖励可叠加).若学校后勤部负责人希望让学生得到更多的奖励,则该负责人应该选择哪一种奖励方案,并说明理由.
参考公式:. ,
, .
.
附表:
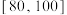 内为成绩优秀.现对参赛的100名学生的竞赛成绩进行统计,得到如下人数分布表.
内为成绩优秀.现对参赛的100名学生的竞赛成绩进行统计,得到如下人数分布表.| 成绩 |  |  |  |  |
| 人数 | 20 | 40 | 30 | 10 |
 列联表,并判断是否有95%的把握认为此次竞赛成绩与该学生是初中生还是高中生有关;
列联表,并判断是否有95%的把握认为此次竞赛成绩与该学生是初中生还是高中生有关;| 优秀 | 非优秀 | 合计 | |
| 初中生 | 20 | ||
| 高中生 | 45 | ||
| 合计 |
方案一:参加了竞赛的学生每人都可抽奖1次,且每次抽奖互不影响,每次中奖的概率均为
 ,抽中奖励价值50元的食堂充值卡,未抽中无奖励;方案二:竞赛成绩优秀的抽奖两次,其余学生抽奖一次,抽奖者点击抽奖按钮,即随机产生一个数字(
,抽中奖励价值50元的食堂充值卡,未抽中无奖励;方案二:竞赛成绩优秀的抽奖两次,其余学生抽奖一次,抽奖者点击抽奖按钮,即随机产生一个数字(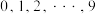 ),若产生的数字能被3整除,则可奖励价值40元的食堂充值卡,否则奖励20元的食堂充值卡(充值卡奖励可叠加).若学校后勤部负责人希望让学生得到更多的奖励,则该负责人应该选择哪一种奖励方案,并说明理由.
),若产生的数字能被3整除,则可奖励价值40元的食堂充值卡,否则奖励20元的食堂充值卡(充值卡奖励可叠加).若学校后勤部负责人希望让学生得到更多的奖励,则该负责人应该选择哪一种奖励方案,并说明理由.参考公式:.
 ,
, .
.附表:
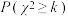 | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
您最近一年使用:0次
名校
7 . 某高新技术企业将产品质量视为企业的生命线,严抓产品质量关. 该企业新研发出了一种产品,该产品由三个电子元件构成,这三个电子元件在生产过程中的次品率分别为 ,
,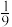 ,
, ,组装过程中不会造成电子元件的损坏,若有一个电子元件是次品,则该产品不能正常工作,即为次品. 现安排质检员对这批产品一一检查,确保无任何一件次品流入市场.
,组装过程中不会造成电子元件的损坏,若有一个电子元件是次品,则该产品不能正常工作,即为次品. 现安排质检员对这批产品一一检查,确保无任何一件次品流入市场.
(1)设 “任取一件产品为次品”,
“任取一件产品为次品”, “该产品仅有一个电子元件是次品”,求
“该产品仅有一个电子元件是次品”,求 ;
;
(2)设一件产品中所含电子元件为次品的个数为 ,求
,求 的分布列和期望;
的分布列和期望;
(3)现有两种方案,方案一:安排三个质检员先行检测这三个元件,次品不进入组装生产线;方案二:安排一个质检员检测成品,一旦发现次品,则取出重新更换次品的电子元件,更换电子元件的费用为20元/个. 已知每个质检员每月的工资为3000元,该企业每月生产该产品 件
件 ,请从企业获益的角度考虑,应该选择选择哪种方案?
,请从企业获益的角度考虑,应该选择选择哪种方案?
 ,
,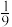 ,
, ,组装过程中不会造成电子元件的损坏,若有一个电子元件是次品,则该产品不能正常工作,即为次品. 现安排质检员对这批产品一一检查,确保无任何一件次品流入市场.
,组装过程中不会造成电子元件的损坏,若有一个电子元件是次品,则该产品不能正常工作,即为次品. 现安排质检员对这批产品一一检查,确保无任何一件次品流入市场.(1)设
 “任取一件产品为次品”,
“任取一件产品为次品”, “该产品仅有一个电子元件是次品”,求
“该产品仅有一个电子元件是次品”,求 ;
;(2)设一件产品中所含电子元件为次品的个数为
 ,求
,求 的分布列和期望;
的分布列和期望;(3)现有两种方案,方案一:安排三个质检员先行检测这三个元件,次品不进入组装生产线;方案二:安排一个质检员检测成品,一旦发现次品,则取出重新更换次品的电子元件,更换电子元件的费用为20元/个. 已知每个质检员每月的工资为3000元,该企业每月生产该产品
 件
件 ,请从企业获益的角度考虑,应该选择选择哪种方案?
,请从企业获益的角度考虑,应该选择选择哪种方案?
您最近一年使用:0次
23-24高二下·全国·期末
8 . 网上购物就是通过互联网检索商品信息,并通过电子订购单发出购物请求,厂商通过邮购的方式发货或通过快递公司送货上门,货到后通过银行转账、微信或支付宝支付等方式在线汇款.根据2019年中国消费者信息研究,超过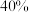 的消费者更加频繁地使用网上购物,使得网上购物和送货上门的需求量激增,越来越多的消费者也首次通过第三方
的消费者更加频繁地使用网上购物,使得网上购物和送货上门的需求量激增,越来越多的消费者也首次通过第三方 、品牌官方网站和微信社群等平台进行购物.某天猫专营店统计了2020年8月5日至9日这5天到该专营店购物的人数
、品牌官方网站和微信社群等平台进行购物.某天猫专营店统计了2020年8月5日至9日这5天到该专营店购物的人数 和时间第
和时间第 天间的数据,列表如表:
天间的数据,列表如表:
(1)由表中给出的数据是否可用线性回归模型拟合人数 与时间
与时间 之间的关系?若可用,估计8月10日到该专营店购物的人数(人数用四舍五入法取整数;若
之间的关系?若可用,估计8月10日到该专营店购物的人数(人数用四舍五入法取整数;若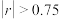 ,则线性相关程度很高,可用线性回归模型拟合,计算
,则线性相关程度很高,可用线性回归模型拟合,计算 时精确到
时精确到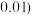 .
.
(2)运用分层抽样的方法从第1天和第5天到该专营店购物的人中随机抽取7人,再从这7人中任取3人进行奖励,求这3人取自不同天的概率;
(3)该专营店为了吸引顾客,推出两种促销方案:方案一,购物金额每满100元可减10元;方案二,一次性购物金额超过800元可抽奖三次,每次中奖的概率均为 ,且每次抽奖互不影响,中奖一次打9折,中奖两次打8折,中奖三次打6折.某顾客计划在此专营店一次性购买1000元的商品,请从实际付款金额的数学期望的角度分析选哪种方案更优惠.
,且每次抽奖互不影响,中奖一次打9折,中奖两次打8折,中奖三次打6折.某顾客计划在此专营店一次性购买1000元的商品,请从实际付款金额的数学期望的角度分析选哪种方案更优惠.
参考数据: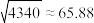 .附:相关系数
.附:相关系数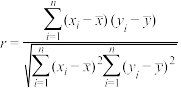 ,回归直线方程的斜率:
,回归直线方程的斜率: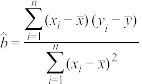 ,
, .
.
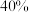 的消费者更加频繁地使用网上购物,使得网上购物和送货上门的需求量激增,越来越多的消费者也首次通过第三方
的消费者更加频繁地使用网上购物,使得网上购物和送货上门的需求量激增,越来越多的消费者也首次通过第三方 、品牌官方网站和微信社群等平台进行购物.某天猫专营店统计了2020年8月5日至9日这5天到该专营店购物的人数
、品牌官方网站和微信社群等平台进行购物.某天猫专营店统计了2020年8月5日至9日这5天到该专营店购物的人数 和时间第
和时间第 天间的数据,列表如表:
天间的数据,列表如表: | 1 | 2 | 3 | 4 | 5 |
 | 75 | 84 | 93 | 98 | 100 |
(1)由表中给出的数据是否可用线性回归模型拟合人数
 与时间
与时间 之间的关系?若可用,估计8月10日到该专营店购物的人数(人数用四舍五入法取整数;若
之间的关系?若可用,估计8月10日到该专营店购物的人数(人数用四舍五入法取整数;若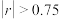 ,则线性相关程度很高,可用线性回归模型拟合,计算
,则线性相关程度很高,可用线性回归模型拟合,计算 时精确到
时精确到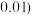 .
.(2)运用分层抽样的方法从第1天和第5天到该专营店购物的人中随机抽取7人,再从这7人中任取3人进行奖励,求这3人取自不同天的概率;
(3)该专营店为了吸引顾客,推出两种促销方案:方案一,购物金额每满100元可减10元;方案二,一次性购物金额超过800元可抽奖三次,每次中奖的概率均为
 ,且每次抽奖互不影响,中奖一次打9折,中奖两次打8折,中奖三次打6折.某顾客计划在此专营店一次性购买1000元的商品,请从实际付款金额的数学期望的角度分析选哪种方案更优惠.
,且每次抽奖互不影响,中奖一次打9折,中奖两次打8折,中奖三次打6折.某顾客计划在此专营店一次性购买1000元的商品,请从实际付款金额的数学期望的角度分析选哪种方案更优惠.参考数据:
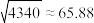 .附:相关系数
.附:相关系数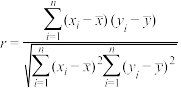 ,回归直线方程的斜率:
,回归直线方程的斜率: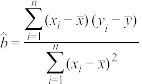 ,
, .
.
您最近一年使用:0次
名校
解题方法
9 . 当前,人工智能技术以前所未有的速度迅猛发展,并逐步影响我们的方方面面,人工智能被认为是推动未来社会发展和解决人类面临的全球性问题的重要手段.某公司在这个领域逐年加大投入,以下是近年来该公司对产品研发年投入额 (单位:百万元)与其年销售量y(单位:千件)的数据统计表.
(单位:百万元)与其年销售量y(单位:千件)的数据统计表.
(1)公司拟分别用①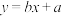 和②
和②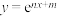 两种方案作为年销售量
两种方案作为年销售量 关于年投入额
关于年投入额 的回归分析模型,请根据已知数据,确定方案①和②的经验回归方程;(
的回归分析模型,请根据已知数据,确定方案①和②的经验回归方程;( 计算过程保留到小数点后两位,最后结果保留到小数点后一位)
计算过程保留到小数点后两位,最后结果保留到小数点后一位)
(2)根据下表数据,用决定系数 (只需比较出大小)比较两种模型的拟合效果哪种更好,并选择拟合精度更高的模型,预测年投入额为
(只需比较出大小)比较两种模型的拟合效果哪种更好,并选择拟合精度更高的模型,预测年投入额为 百万元时,产品的销售量是多少?
百万元时,产品的销售量是多少?
参考公式及数据: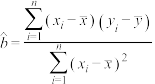 ,
, ,
,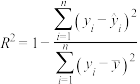 ,
,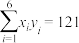 ,
,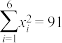 ,
,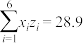 ,
,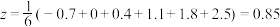 ,
,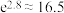 ,
,  .
.
 (单位:百万元)与其年销售量y(单位:千件)的数据统计表.
(单位:百万元)与其年销售量y(单位:千件)的数据统计表.
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 1 | 1.5 | 3 | 6 | 12 |
|
|
|
|
|
|
|
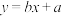 和②
和②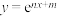 两种方案作为年销售量
两种方案作为年销售量 关于年投入额
关于年投入额 的回归分析模型,请根据已知数据,确定方案①和②的经验回归方程;(
的回归分析模型,请根据已知数据,确定方案①和②的经验回归方程;(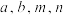 计算过程保留到小数点后两位,最后结果保留到小数点后一位)
计算过程保留到小数点后两位,最后结果保留到小数点后一位)(2)根据下表数据,用决定系数
 (只需比较出大小)比较两种模型的拟合效果哪种更好,并选择拟合精度更高的模型,预测年投入额为
(只需比较出大小)比较两种模型的拟合效果哪种更好,并选择拟合精度更高的模型,预测年投入额为 百万元时,产品的销售量是多少?
百万元时,产品的销售量是多少?经验回归方程 |
|
|
残差平方和 |
|
|
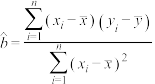 ,
, ,
,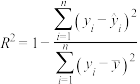 ,
,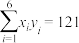 ,
,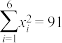 ,
,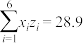 ,
,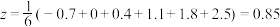 ,
,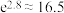 ,
,  .
.
您最近一年使用:0次
2024-02-20更新
|
2258次组卷
|
11卷引用:第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)专题8.2 一元线性回归模型及其应用【七大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第八章 成对数据的统计分析总结 第二课提炼本章思想(已下线)第八章:成对数据的统计分析章末重点题型复习(5题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题8.6 成对数据的统计分析全章八大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)辽宁省大连市第二十四中学2023-2024学年高二下学期期中考试数学试卷(已下线)专题06 统计模型的热点题型(7类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)专题07 线性回归分析与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)重庆市第一中学校2023-2024学年高三下学期2月开学考试数学试卷(已下线)专题08 统计案例分析(讲义)
2024高三·全国·专题练习
名校
10 . 某短视频软件经过几年的快速发展,深受人们的喜爱,该软件除了有娱乐属性外,也可通过平台推送广告.某公司为了宣传新产品,现有以下两种宣传方案:
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且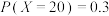 ,期望
,期望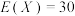 .
.
方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为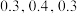 .
.
(1)请写出方案一的分布列,并求方差 ;
;
(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且
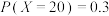 ,期望
,期望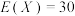 .
.方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为
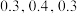 .
.(1)请写出方案一的分布列,并求方差
 ;
;(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
您最近一年使用:0次
2024-01-07更新
|
608次组卷
|
7卷引用:7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)
(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题7.7 随机变量及其分布全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)广东省东莞市七校2023-2024学年高二下学期5月联考数学试题陕西省咸阳市武功县普集高级中学2023-2024学年高二下学期6月月考数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)(已下线)专题02 结论探索型【练】【北京版】