1 . 如图,某地一天中6~14时的温度变化曲线近似满足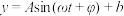 (
( ,
, ,
,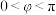 ).
).
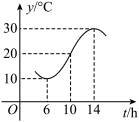
(1)求出这段曲线的函数解析式;
(2)某行业在该地经营,当温度在区间 之间时为最佳营业时间,那么该行业在6~14时,最佳营业时间有多少小时?
之间时为最佳营业时间,那么该行业在6~14时,最佳营业时间有多少小时?
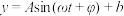 (
( ,
, ,
,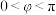 ).
).
(1)求出这段曲线的函数解析式;
(2)某行业在该地经营,当温度在区间
 之间时为最佳营业时间,那么该行业在6~14时,最佳营业时间有多少小时?
之间时为最佳营业时间,那么该行业在6~14时,最佳营业时间有多少小时?
您最近一年使用:0次
2023-02-05更新
|
519次组卷
|
3卷引用:沪教版(2020) 一轮复习 堂堂清 第三单元 3.8 三角函数的图像与性质(二)
沪教版(2020) 一轮复习 堂堂清 第三单元 3.8 三角函数的图像与性质(二)四川省江油市太白中学2023-2024学年高二上学期入学考试数学试题(已下线)广东实验中学2024届高三上学期第一次阶段考试数学试题变式题15-18
名校
2 . 在 中,
中,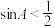 是
是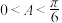 的( )
的( )
 中,
中,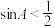 是
是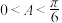 的( )
的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
名校
3 . 如图,一个大风车的半径为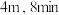 旋转一周,它的最低点
旋转一周,它的最低点 离地面
离地面 ,它的右侧有一点
,它的右侧有一点 且距离地面
且距离地面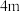 .风车翼片的一个端点
.风车翼片的一个端点 从
从 开始计时,按逆时针方向旋转.
开始计时,按逆时针方向旋转.

(1)试写出点 距离地面的高度
距离地面的高度 关于时刻
关于时刻 (min)的函数关系式
(min)的函数关系式 ;
;
(2)在点 旋转一周的时间内,有多长时间点
旋转一周的时间内,有多长时间点 距离地面超过
距离地面超过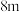 ?
?
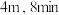 旋转一周,它的最低点
旋转一周,它的最低点 离地面
离地面 ,它的右侧有一点
,它的右侧有一点 且距离地面
且距离地面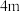 .风车翼片的一个端点
.风车翼片的一个端点 从
从 开始计时,按逆时针方向旋转.
开始计时,按逆时针方向旋转.
(1)试写出点
 距离地面的高度
距离地面的高度 关于时刻
关于时刻 (min)的函数关系式
(min)的函数关系式 ;
;(2)在点
 旋转一周的时间内,有多长时间点
旋转一周的时间内,有多长时间点 距离地面超过
距离地面超过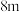 ?
?
您最近一年使用:0次
2023-01-13更新
|
593次组卷
|
4卷引用:第一章 三角函数(基础检测卷)
第一章 三角函数(基础检测卷)(已下线)1.8 三角函数的简单应用(课件+练习)河南省驻马店高级中学2022-2023学年高一下学期第一次月考数学试题江苏省盐城市上冈高级中学等2022-2023学年高一上学期期末联考数学试题
4 . 某港口的水深 (米)是时间
(米)是时间 (
(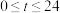 ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
经过长期观测,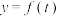 可近似的看成是函数
可近似的看成是函数
(1)根据以上数据,求出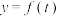 的解析式;
的解析式;
(2)若船舶航行时,水深至少要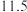 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
 (米)是时间
(米)是时间 (
(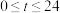 ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表: | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
 | 10 | 13 |  | 7 | 10 | 13 | 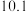 | 7 | 10 |
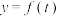 可近似的看成是函数
可近似的看成是函数
(1)根据以上数据,求出
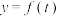 的解析式;
的解析式;(2)若船舶航行时,水深至少要
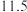 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
您最近一年使用:0次
2023-01-07更新
|
427次组卷
|
4卷引用:广东省惠州市光正实验学校2022-2023学年高一下学期3月月考数学试题
广东省惠州市光正实验学校2022-2023学年高一下学期3月月考数学试题(已下线)1.8 三角函数的简单应用(课件+练习)(已下线)第30讲 三角函数的应用-【暑假自学课】(人教A版2019必修第一册)广西桂林市逸仙中学2021-2022学年高一下学期期中考试数学试题
解题方法
5 . 已知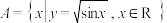 ,
, ,求
,求 .
.
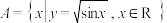 ,
, ,求
,求 .
.
您最近一年使用:0次
6 . 已知函数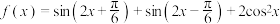 .
.
(1)求 的最小值及最小正周期;
的最小值及最小正周期;
(2)求使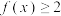 的x的取值范围.
的x的取值范围.
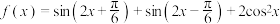 .
.(1)求
 的最小值及最小正周期;
的最小值及最小正周期;(2)求使
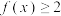 的x的取值范围.
的x的取值范围.
您最近一年使用:0次
7 . 已知 .
.
(1)求函数在 上的单调递减区间;
上的单调递减区间;
(2)求函数在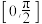 上的值域;
上的值域;
(3)求不等式 在
在 上的解集.
上的解集.
 .
.(1)求函数在
 上的单调递减区间;
上的单调递减区间;(2)求函数在
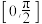 上的值域;
上的值域;(3)求不等式
 在
在 上的解集.
上的解集.
您最近一年使用:0次
2023-01-01更新
|
1651次组卷
|
5卷引用:安徽省滁州市定远县民族中学2022-2023学年高一上学期12月月考数学试题
8 . 若 ,在
,在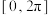 上满足
上满足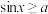 的x的范围是( )
的x的范围是( )
 ,在
,在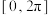 上满足
上满足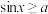 的x的范围是( )
的x的范围是( )A. | B.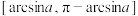 | C.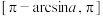 | D.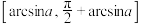 |
您最近一年使用:0次
名校
解题方法
9 . 在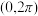 内,使
内,使 成立的x取值范围不是( )
成立的x取值范围不是( )
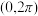 内,使
内,使 成立的x取值范围不是( )
成立的x取值范围不是( )A. | B.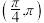 |
C.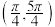 | D.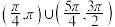 |
您最近一年使用:0次
名校
10 . 已知函数 的部分图象如图所示,下列说法不正确的是( ).
的部分图象如图所示,下列说法不正确的是( ).
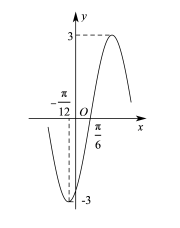
 的部分图象如图所示,下列说法不正确的是( ).
的部分图象如图所示,下列说法不正确的是( ).
A. 的最小正周期为 的最小正周期为 |
B. |
C. 的解集为 的解集为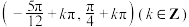 |
D.将 的图象向左平移 的图象向左平移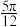 个单位长度后得到的图象关于原点对称 个单位长度后得到的图象关于原点对称 |
您最近一年使用:0次



