1 . 已知函数 .
.
(1)求 的最小正周期和对称轴;
的最小正周期和对称轴;
(2)求 的单调递增区间;
的单调递增区间;
(3)当 时,求
时,求 的最大值和最小值.
的最大值和最小值.
 .
.(1)求
 的最小正周期和对称轴;
的最小正周期和对称轴;(2)求
 的单调递增区间;
的单调递增区间;(3)当
 时,求
时,求 的最大值和最小值.
的最大值和最小值.
您最近一年使用:0次
解题方法
2 . 已知集合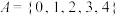 ,
,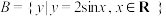 ,则
,则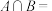 ( )
( )
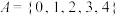 ,
,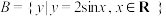 ,则
,则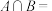 ( )
( )A. | B.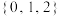 | C.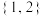 | D.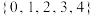 |
您最近一年使用:0次
7日内更新
|
83次组卷
|
2卷引用: 河南省南阳市第二中学校2022-2023学年高一下学期期中考试数学试题
名校
3 . 欧拉公式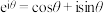 把自然对数的底数
把自然对数的底数 、虚数单位
、虚数单位 、三角函数联系在一起,被誉为“数学中的天桥”.若复数
、三角函数联系在一起,被誉为“数学中的天桥”.若复数 满足
满足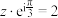 ,则
,则 的取值范围为( )
的取值范围为( )
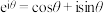 把自然对数的底数
把自然对数的底数 、虚数单位
、虚数单位 、三角函数联系在一起,被誉为“数学中的天桥”.若复数
、三角函数联系在一起,被誉为“数学中的天桥”.若复数 满足
满足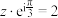 ,则
,则 的取值范围为( )
的取值范围为( )A.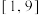 | B.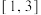 | C.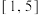 | D. |
您最近一年使用:0次
解题方法
4 . 已知函数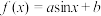 的最大值是1,最小值是–7,求函数
的最大值是1,最小值是–7,求函数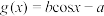 的最大值.
的最大值.
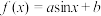 的最大值是1,最小值是–7,求函数
的最大值是1,最小值是–7,求函数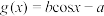 的最大值.
的最大值.
您最近一年使用:0次
解题方法
5 . 已知函数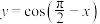 ,
,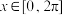 ,则该函数图象的最低点的坐标为
,则该函数图象的最低点的坐标为___________ .
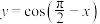 ,
,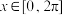 ,则该函数图象的最低点的坐标为
,则该函数图象的最低点的坐标为
您最近一年使用:0次
6 . 求下列函数的值域.
(1)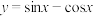 ,
,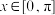 ;
;
(2)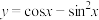 .
.
(1)
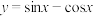 ,
,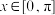 ;
;(2)
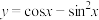 .
.
您最近一年使用:0次
名校
7 . 已知向量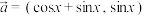 ,
,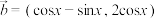 ,设
,设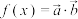 ,
, .
.
(1)求函数 的单调递增区间和对称中心坐标;
的单调递增区间和对称中心坐标;
(2)当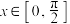 时,求函数
时,求函数 的最大值及最小值.
的最大值及最小值.
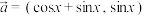 ,
,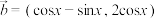 ,设
,设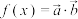 ,
, .
.(1)求函数
 的单调递增区间和对称中心坐标;
的单调递增区间和对称中心坐标;(2)当
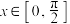 时,求函数
时,求函数 的最大值及最小值.
的最大值及最小值.
您最近一年使用:0次
8 . 已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)当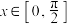 时,求函数
时,求函数 的最大值,以及相应
的最大值,以及相应 的值.
的值.
 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)当
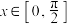 时,求函数
时,求函数 的最大值,以及相应
的最大值,以及相应 的值.
的值.
您最近一年使用:0次
9 . 已知函数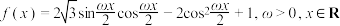 ,在曲线
,在曲线 与直线
与直线 的交点中,若相邻交点的距离为
的交点中,若相邻交点的距离为 .
.
(1)求函数 的解析式;
的解析式;
(2)若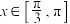 ,解不等式
,解不等式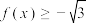 ;
;
(3)若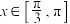 ,且关于
,且关于 的方程
的方程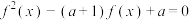 有三个不等的实根,求实数
有三个不等的实根,求实数 的取值范围.
的取值范围.
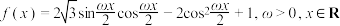 ,在曲线
,在曲线 与直线
与直线 的交点中,若相邻交点的距离为
的交点中,若相邻交点的距离为 .
.(1)求函数
 的解析式;
的解析式;(2)若
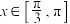 ,解不等式
,解不等式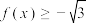 ;
;(3)若
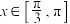 ,且关于
,且关于 的方程
的方程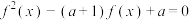 有三个不等的实根,求实数
有三个不等的实根,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-07-13更新
|
377次组卷
|
2卷引用:湖北省孝感市重点高中教科研协作体2023-2024学年高一下学期期中考试数学试卷
名校
10 . 已知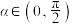 ,若
,若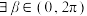 ,使
,使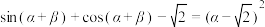 成立,则
成立,则
__________ .
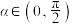 ,若
,若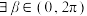 ,使
,使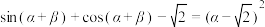 成立,则
成立,则
您最近一年使用:0次
2024-07-11更新
|
401次组卷
|
4卷引用:2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题
2025届甘肃省张掖市某校高三下学期6月模拟考试数学试题(已下线)模型7 三角函数运用构造法化简模型问题(第4章 三角函数与解三角形 )辽宁省教研教改联合体2025届高三第一次调研考试数学试题(已下线)第02讲 三角恒等变换(十一大题型)(练习)



