解题方法
1 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察:(2)整体设元;(3)整体代入:(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
阅读材料二:解决多元变量问题时,其中一种思路是运用消元思想将多元问题转化为一元问题,再结合一元问题处理方法进行研究.
例如,正实数 满足
满足 ,求
,求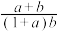 的最小值.
的最小值.
解:由 ,得
,得 ,
,
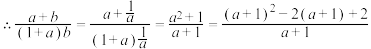
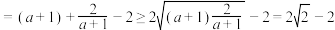 ,
,
当且仅当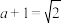 ,即
,即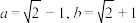 时,等号成立.
时,等号成立.
 的最小值为
的最小值为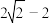 .
.
波利亚在《怎样解题》中指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
结合阅读材料解答下列问题:
(1)已知
 ,求
,求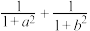 的值;
的值;(2)若正实数
 满足
满足 ,求
,求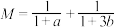 的最小值.
的最小值.
您最近一年使用:0次
名校
解题方法
2 . 已知函数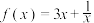 .
.
(1)判断 在
在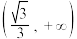 上的单调性,并证明;
上的单调性,并证明;
(2)若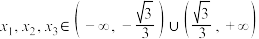 ,且
,且 ,
, ,
, 都为正数,求证:
都为正数,求证: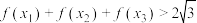 .
.
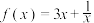 .
.(1)判断
 在
在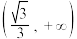 上的单调性,并证明;
上的单调性,并证明;(2)若
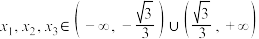 ,且
,且 ,
, ,
, 都为正数,求证:
都为正数,求证: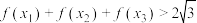 .
.
您最近一年使用:0次
2024-01-26更新
|
199次组卷
|
2卷引用:江苏省泰州市2023-2024学年高一上学期1月期末调研数学试题
名校
3 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.
例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵ ,∴
,∴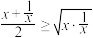 ,即
,即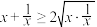 ,∴
,∴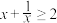 ,当且仅当
,当且仅当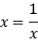 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)已知如 ,求下列各式的值:
,求下列各式的值: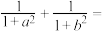
___________ .
(2)若正数 满足
满足 ,则
,则 的最小值为
的最小值为___________ .
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入;(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
阅读材料二:基本不等式
 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.
时等号成立,它是解决最值问题的有力工具.例如:在
 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵
 ,∴
,∴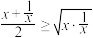 ,即
,即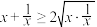 ,∴
,∴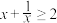 ,当且仅当
,当且仅当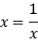 ,即
,即 时,
时, 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)已知如
 ,求下列各式的值:
,求下列各式的值: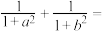
(2)若正数
 满足
满足 ,则
,则 的最小值为
的最小值为
您最近一年使用:0次
名校
解题方法
4 . 问题:已知 均为正实数,且
均为正实数,且 ,求证:
,求证: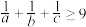 .
.
证明: ,当且仅当
,当且仅当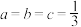 时,等号成立.学习上述解法并解决下列问题:
时,等号成立.学习上述解法并解决下列问题:
(1)若实数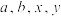 满足
满足 ,试比较
,试比较 和
和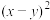 的大小,并说明理由;
的大小,并说明理由;
(2)求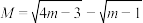 的最小值,并求出使得
的最小值,并求出使得 最小的
最小的 的值.
的值.
 均为正实数,且
均为正实数,且 ,求证:
,求证: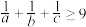 .
.证明:
 ,当且仅当
,当且仅当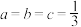 时,等号成立.学习上述解法并解决下列问题:
时,等号成立.学习上述解法并解决下列问题:(1)若实数
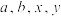 满足
满足 ,试比较
,试比较 和
和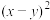 的大小,并说明理由;
的大小,并说明理由;(2)求
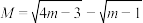 的最小值,并求出使得
的最小值,并求出使得 最小的
最小的 的值.
的值.
您最近一年使用:0次
名校
5 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法,
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如, ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
请根据阅读材料解答下列问题
(1)已知如 ,求
,求 ___________.
___________.
(2)若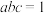 ,解方程
,解方程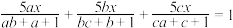 .
.
(3)若正数 、
、 满足
满足 ,求
,求 的最小值.
的最小值.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如,
 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
请根据阅读材料解答下列问题
(1)已知如
 ,求
,求 ___________.
___________.(2)若
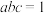 ,解方程
,解方程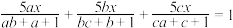 .
.(3)若正数
 、
、 满足
满足 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2023-10-17更新
|
227次组卷
|
2卷引用:重庆市第十一中学校2023-2024学年高一上学期10月月考数学试题
名校
解题方法
6 . 已知a、b为正数.
(1)已知 ,求证:
,求证: ;
;
(2)若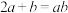 ,证明:
,证明: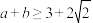 .
.
(1)已知
 ,求证:
,求证: ;
;(2)若
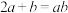 ,证明:
,证明: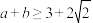 .
.
您最近一年使用:0次
名校
解题方法
7 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂,从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是发现新问题、新结论的重要方法.
例如,已知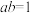 ,求证:
,求证: .
.
证明:原式 .
.
波利亚在《怎样解题》中也指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总是成群生长.”类似上述问题,我们有更多的式子满足以上特征.
请根据上述材料解答下列问题:
(1)已知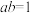 ,求
,求 的值;
的值;
(2)若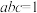 ,解方程
,解方程 ;
;
(3)若正数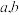 满足
满足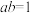 ,求
,求 的最小值.
的最小值.
例如,已知
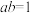 ,求证:
,求证: .
.证明:原式
 .
.波利亚在《怎样解题》中也指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总是成群生长.”类似上述问题,我们有更多的式子满足以上特征.
请根据上述材料解答下列问题:
(1)已知
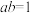 ,求
,求 的值;
的值;(2)若
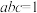 ,解方程
,解方程 ;
;(3)若正数
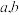 满足
满足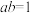 ,求
,求 的最小值.
的最小值.
您最近一年使用:0次
2022-10-21更新
|
437次组卷
|
4卷引用:广东省中山市2022-2023学年高一上学期第一次调研数学试题
广东省中山市2022-2023学年高一上学期第一次调研数学试题四川省成都市第七中学2023年高三上学期1月月考数学文科试题四川省攀枝花市第三高级中学校2023-2024学年高一上学期10月月考数学试题(已下线)第03讲 第二章 一元二次函数、方程和不等式章节综合测试-【练透核心考点】
名校
解题方法
8 . 记 的内角
的内角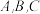 所对的边分别为
所对的边分别为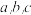 ,已知
,已知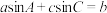 .
.
(1)求证: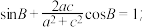
(2)若 的面积
的面积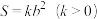 ,求
,求 的最大值,并证明:当
的最大值,并证明:当 取最大值时,
取最大值时, 为直角三角形.
为直角三角形.
 的内角
的内角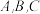 所对的边分别为
所对的边分别为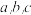 ,已知
,已知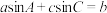 .
.(1)求证:
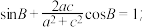
(2)若
 的面积
的面积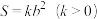 ,求
,求 的最大值,并证明:当
的最大值,并证明:当 取最大值时,
取最大值时, 为直角三角形.
为直角三角形.
您最近一年使用:0次
2022-12-06更新
|
755次组卷
|
3卷引用:安徽省皖优联盟2022-2023学年高三上学期12月第二次阶段性联考数学试题
名校
9 . 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法.阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察:(2)整体设元:(3)整体代入:(4)整体求和等.例如,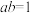 ,求证:
,求证: .证明:原式
.证明:原式 .波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.例如:在
时等号成立,它是解决最值问题的有力工具.例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
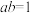 ,求证:
,求证: .证明:原式
.证明:原式 .波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式
.波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.阅读材料二:基本不等式 ,当且仅当
,当且仅当 时等号成立,它是解决最值问题的有力工具.例如:在
时等号成立,它是解决最值问题的有力工具.例如:在 的条件下,当x为何值时,
的条件下,当x为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
您最近一年使用:0次
名校
10 . 若函数 对任意的
对任意的 均有
均有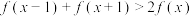 ,则称函数具有性质
,则称函数具有性质 .
.
(1)判断下面函数①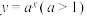 ;②
;②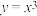 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;
(2)全集为 ,函数
,函数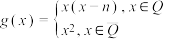 ,试判断并证明函数
,试判断并证明函数 是否具有性质
是否具有性质 ;
;
(3)若函数 具有性质
具有性质 ,且
,且 ,求证:是否对任意
,求证:是否对任意 ,
,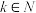 均有
均有
 对任意的
对任意的 均有
均有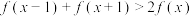 ,则称函数具有性质
,则称函数具有性质 .
.(1)判断下面函数①
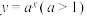 ;②
;②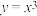 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(2)全集为
 ,函数
,函数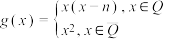 ,试判断并证明函数
,试判断并证明函数 是否具有性质
是否具有性质 ;
;(3)若函数
 具有性质
具有性质 ,且
,且 ,求证:是否对任意
,求证:是否对任意 ,
,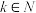 均有
均有
您最近一年使用:0次
2021-11-23更新
|
864次组卷
|
2卷引用:上海市七宝中学2021-2022学年高一上学期期中数学试题



