名校
1 . 在正三棱柱 中,
中, 为棱
为棱 的中点,如图所示.
的中点,如图所示.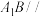 平面
平面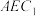 ;
;
(2)若二面角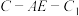 的大小为
的大小为 ,求直线
,求直线 和平面
和平面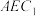 所成角的正弦值.
所成角的正弦值.
 中,
中, 为棱
为棱 的中点,如图所示.
的中点,如图所示.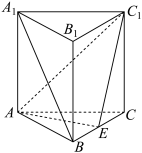
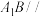 平面
平面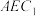 ;
;(2)若二面角
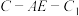 的大小为
的大小为 ,求直线
,求直线 和平面
和平面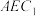 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-08-20更新
|
720次组卷
|
3卷引用:【巩固卷】综合检测试卷(二)单元测试A-湘教版(2019)必修(第二册)
【巩固卷】综合检测试卷(二)单元测试A-湘教版(2019)必修(第二册)(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2黑龙江省绥化市第二中学2024-2025学年高二上学期开学考数学试卷
2 . 已知点 是边长为2的菱形
是边长为2的菱形 所在平面外一点,且点P在底面
所在平面外一点,且点P在底面 上的射影是
上的射影是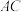 与
与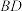 的交点
的交点 .已知
.已知 ,
, 是等边三角形.
是等边三角形.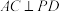 ;
;
(2)求点 到平面
到平面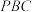 的距离;
的距离;
(3)若点 是线段
是线段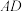 上的动点.问:点
上的动点.问:点 在何处时,直线
在何处时,直线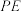 与平面
与平面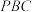 所成的角最大?求出这个最大角,并说明点
所成的角最大?求出这个最大角,并说明点 此时所在的位置.
此时所在的位置.
 是边长为2的菱形
是边长为2的菱形 所在平面外一点,且点P在底面
所在平面外一点,且点P在底面 上的射影是
上的射影是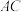 与
与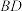 的交点
的交点 .已知
.已知 ,
, 是等边三角形.
是等边三角形.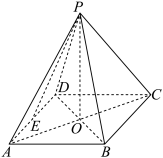
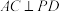 ;
;(2)求点
 到平面
到平面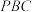 的距离;
的距离;(3)若点
 是线段
是线段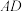 上的动点.问:点
上的动点.问:点 在何处时,直线
在何处时,直线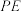 与平面
与平面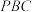 所成的角最大?求出这个最大角,并说明点
所成的角最大?求出这个最大角,并说明点 此时所在的位置.
此时所在的位置.
您最近一年使用:0次
2024-08-02更新
|
204次组卷
|
2卷引用:【基础卷】 期末测试 单元测试C-沪教版(2020)必修第三册
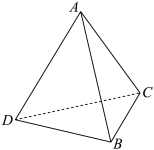
3 . 在四面体 中,钝角
中,钝角 的三边均为整数且满足
的三边均为整数且满足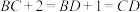 .
. 的外接圆半径.
的外接圆半径.
(2)(i)设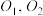 分别为
分别为 ,
,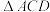 的外心,过
的外心,过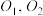 分别作平面BCD,平面ACD的垂线l,m,求证:直线l,m相交于一点.
分别作平面BCD,平面ACD的垂线l,m,求证:直线l,m相交于一点.
(ii)若四面体的外接球O的半径为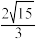 ,设
,设 的外接圆圆心为
的外接圆圆心为 ,延长
,延长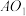 交球面于点M,
交球面于点M, 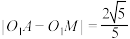 ,求直线AM与平面BCD所成角的正弦值.
,求直线AM与平面BCD所成角的正弦值.
 中,钝角
中,钝角 的三边均为整数且满足
的三边均为整数且满足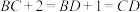 .
.
 的外接圆半径.
的外接圆半径.(2)(i)设
 分别为
分别为 ,
, 的外心,过
的外心,过 分别作平面BCD,平面ACD的垂线l,m,求证:直线l,m相交于一点.
分别作平面BCD,平面ACD的垂线l,m,求证:直线l,m相交于一点.(ii)若四面体的外接球O的半径为
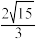 ,设
,设 的外接圆圆心为
的外接圆圆心为 ,延长
,延长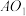 交球面于点M,
交球面于点M, 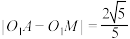 ,求直线AM与平面BCD所成角的正弦值.
,求直线AM与平面BCD所成角的正弦值.
您最近一年使用:0次
名校
解题方法
4 . 如图,在四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, 底面
底面 ,
, ,
, 分别为线段
分别为线段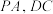 的中点.
的中点.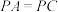 ;
;
(2)证明: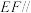 平面
平面 ;
;
(3)若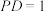 ,
,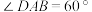 ,记
,记 与平面
与平面 所成角为
所成角为 ,求
,求 的最大值.
的最大值.
 中,底面
中,底面 为平行四边形,
为平行四边形, 底面
底面 ,
, ,
, 分别为线段
分别为线段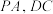 的中点.
的中点.
 ;
;(2)证明:
 平面
平面 ;
;(3)若
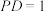 ,
,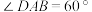 ,记
,记 与平面
与平面 所成角为
所成角为 ,求
,求 的最大值.
的最大值.
您最近一年使用:0次
2024-09-15更新
|
433次组卷
|
2卷引用:安徽省马鞍山市第二中学2023-2024学年高一下学期期末教学质量监测数学试题
名校
解题方法
5 . 如图所示,已知 平面ABC,
平面ABC, ∥
∥ ,
, ,
, ,
,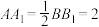 ,E为BC的中点.
,E为BC的中点.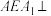 平面
平面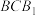 ;
;
(2)求直线 与平面
与平面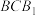 所成角的大小.
所成角的大小.
 平面ABC,
平面ABC, ∥
∥ ,
, ,
, ,
,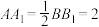 ,E为BC的中点.
,E为BC的中点.
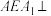 平面
平面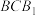 ;
;(2)求直线
 与平面
与平面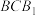 所成角的大小.
所成角的大小.
您最近一年使用:0次
名校
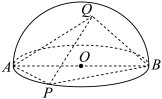
6 . 如图, 是半球O的直径,P是半球底面圆周上一点,Q是半球面上一点,且
是半球O的直径,P是半球底面圆周上一点,Q是半球面上一点,且 .
. ;
;
(2)若 ,求直线
,求直线 与平面
与平面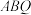 所成角的正弦值.
所成角的正弦值.
 是半球O的直径,P是半球底面圆周上一点,Q是半球面上一点,且
是半球O的直径,P是半球底面圆周上一点,Q是半球面上一点,且 .
.
 ;
;(2)若
 ,求直线
,求直线 与平面
与平面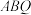 所成角的正弦值.
所成角的正弦值.
您最近一年使用:0次
2024-09-04更新
|
601次组卷
|
3卷引用:广东省广州市越秀区2023-2024学年高一下学期期末数学试题
广东省广州市越秀区2023-2024学年高一下学期期末数学试题(已下线)重难点突破02 利用传统方法求线线角、线面角、二面角与距离 (九大题型)-2安徽省宣城中学2024-2025学年高二上学期开学测试数学试题
名校
7 . 已知正方体 的棱长为
的棱长为 ,
, 是线段
是线段 上的动点,则( )
上的动点,则( )
 的棱长为
的棱长为 ,
, 是线段
是线段 上的动点,则( )
上的动点,则( )A. |
B.二面角 的正切值为 的正切值为 |
C.直线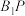 与平面 与平面 所成最小角的正弦值为 所成最小角的正弦值为 |
D.若 是对角线 是对角线 上一点,则 上一点,则 的最小值为 的最小值为 |
您最近一年使用:0次
2024-09-04更新
|
442次组卷
|
2卷引用:山东省威海市2023-2024学年高一下学期期末考试数学试题
名校
8 . 如图甲,在 中,
中, ,
, 为
为 的中点,
的中点, 为
为 上一点,且满足
上一点,且满足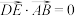 ,将
,将 沿
沿 翻折得到直二面角
翻折得到直二面角 ,连接
,连接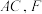 是
是 的中点,连接
的中点,连接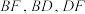 (如图乙所示),则下列结论正确的是( )
(如图乙所示),则下列结论正确的是( )
 中,
中, ,
, 为
为 的中点,
的中点, 为
为 上一点,且满足
上一点,且满足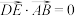 ,将
,将 沿
沿 翻折得到直二面角
翻折得到直二面角 ,连接
,连接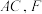 是
是 的中点,连接
的中点,连接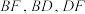 (如图乙所示),则下列结论正确的是( )
(如图乙所示),则下列结论正确的是( )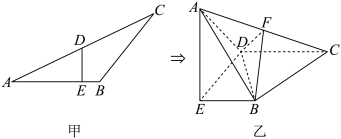
A. | B. ∥平面 ∥平面 |
C. 与平面 与平面 所成角的正切值是 所成角的正切值是 | D.三棱锥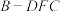 的体积为 的体积为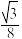 |
您最近一年使用:0次
2024-09-02更新
|
394次组卷
|
2卷引用:云南省昆明市官渡区云南大学附属中学星耀学校2023-2024学年高一下学期市统测模拟考试数学试题
名校
9 . 如图,在正方体 中,
中, 为线段
为线段 的中点,
的中点, 为线段
为线段 上的动点.则下列结论正确的是( )
上的动点.则下列结论正确的是( )
 中,
中, 为线段
为线段 的中点,
的中点, 为线段
为线段 上的动点.则下列结论正确的是( )
上的动点.则下列结论正确的是( )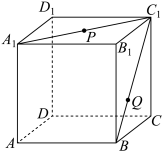
A.若 为 为 中点,则 中点,则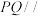 平面 平面 |
B.若 为 为 中点,则 中点,则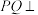 平面 平面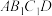 |
C.不存在点 ,使得 ,使得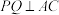 |
D.PQ与平面 所成角的正弦值的取值范围为 所成角的正弦值的取值范围为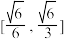 |
您最近一年使用:0次
2024-08-28更新
|
305次组卷
|
2卷引用:黑龙江省哈尔滨市第四中学校2023-2024学年高一下学期期末考试数学试卷
名校
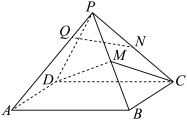
10 . 如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,M,N分别是棱PB,PC的中点, 是棱PA上一点,且
是棱PA上一点,且 .
.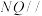 平面MCD;
平面MCD;
(2)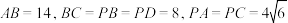 ,求直线PA与平面PBC所成角的正弦值.
,求直线PA与平面PBC所成角的正弦值.
 是棱PA上一点,且
是棱PA上一点,且 .
.
 平面MCD;
平面MCD;(2)
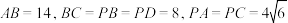 ,求直线PA与平面PBC所成角的正弦值.
,求直线PA与平面PBC所成角的正弦值.
您最近一年使用:0次



