1 . 在平面直角坐标系xOy中,曲线C的参数方程为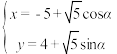 (α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
.
(1)求C与l的直角坐标方程;
(2)若P是C上的一个动点,求P到l的距离的取值范围.
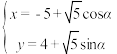 (α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
.(1)求C与l的直角坐标方程;
(2)若P是C上的一个动点,求P到l的距离的取值范围.
您最近一年使用:0次
2024-04-22更新
|
259次组卷
|
3卷引用:四川省资阳市2024届高三适应性考试(二模)数学试题
2 . 在直角坐标系 中,已知圆
中,已知圆 的方程为:
的方程为: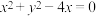 .
.
(1)写出圆 的一个参数方程;
的一个参数方程;
(2)若 ,
, 是圆
是圆 上不同的两点,且
上不同的两点,且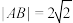 ,求
,求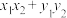 的最大值.
的最大值.
 中,已知圆
中,已知圆 的方程为:
的方程为: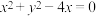 .
.(1)写出圆
 的一个参数方程;
的一个参数方程;(2)若
 ,
, 是圆
是圆 上不同的两点,且
上不同的两点,且 ,求
,求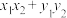 的最大值.
的最大值.
您最近一年使用:0次
名校
解题方法
3 . 已知椭圆 的一个焦点为
的一个焦点为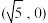 ,离心率为
,离心率为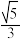 ,点P为圆
,点P为圆 上任意一点,
上任意一点, 为坐标原点.
为坐标原点.
(1)记线段OP与椭圆C的交点为Q,求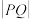 的取值范围;
的取值范围;
(2)设直线l经过点P,且与椭圆C相切,与圆M相交于另一点A,点A关于原点的对称点为B,试判断直线PB与椭圆C的位置关系,并证明你的结论.
 的一个焦点为
的一个焦点为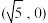 ,离心率为
,离心率为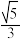 ,点P为圆
,点P为圆 上任意一点,
上任意一点, 为坐标原点.
为坐标原点.(1)记线段OP与椭圆C的交点为Q,求
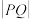 的取值范围;
的取值范围;(2)设直线l经过点P,且与椭圆C相切,与圆M相交于另一点A,点A关于原点的对称点为B,试判断直线PB与椭圆C的位置关系,并证明你的结论.
您最近一年使用:0次
4 . 已知直线 的参数方程为
的参数方程为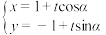 (其中
(其中 为参数),以原点
为参数),以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为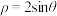 .
.
(1)若点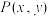 在直线
在直线 上,且
上,且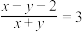 ,求直线
,求直线 的斜率;
的斜率;
(2)若 ,求曲线
,求曲线 上的点到直线
上的点到直线 的距离的最大值.
的距离的最大值.
 的参数方程为
的参数方程为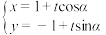 (其中
(其中 为参数),以原点
为参数),以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为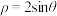 .
.(1)若点
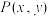 在直线
在直线 上,且
上,且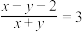 ,求直线
,求直线 的斜率;
的斜率;(2)若
 ,求曲线
,求曲线 上的点到直线
上的点到直线 的距离的最大值.
的距离的最大值.
您最近一年使用:0次
2020-08-16更新
|
377次组卷
|
8卷引用:四川省宜宾市第四中学校2020届高三第一次高考适应性考试数学(理)试题
四川省宜宾市第四中学校2020届高三第一次高考适应性考试数学(理)试题四川省宜宾市第四中学校2020届高三第一次高考适应性考试数学(文)试题2020届安徽省皖江名校联盟高三下学期第五次联考数学(文)试题2020届安徽省皖江名校联盟高三下学期第五次联考数学(理)试题(已下线)专题22 坐标系与参数方程-2020年高考数学(理)母题题源解密(全国Ⅱ专版)(已下线)专题22 坐标系与参数方程-2020年高考数学(文)母题题源解密(全国Ⅱ专版)河南省郑州市第一中学2020-2021学年高三上学期开学测试数学(理)河南省郑州市第一中学2020-2021学年高三上学期开学测试数学(文)
5 . 在平面直角坐标系 中,曲线
中,曲线 的参数方程为:
的参数方程为: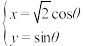 (
( 为参数).以原点
为参数).以原点 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 的极坐标方程为
的极坐标方程为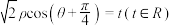 .
.
(1)若 ,分别求出曲线
,分别求出曲线 和直线
和直线 的直角坐标方程;
的直角坐标方程;
(2)令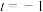 ,求曲线
,求曲线 上的点到直线
上的点到直线 的最大距离.
的最大距离.
 中,曲线
中,曲线 的参数方程为:
的参数方程为: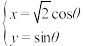 (
( 为参数).以原点
为参数).以原点 为极点,
为极点, 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线 的极坐标方程为
的极坐标方程为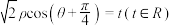 .
.(1)若
 ,分别求出曲线
,分别求出曲线 和直线
和直线 的直角坐标方程;
的直角坐标方程;(2)令
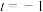 ,求曲线
,求曲线 上的点到直线
上的点到直线 的最大距离.
的最大距离.
您最近一年使用:0次
2020-03-24更新
|
159次组卷
|
2卷引用:2019届四川省凉山州高三第三次诊断性检测数学(理)试题
6 . 已知圆 以点
以点 为圆心,并且经过坐标原点
为圆心,并且经过坐标原点 ,设直线
,设直线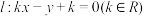 与圆
与圆 相交于
相交于 两点.
两点.
(Ⅰ)求圆 的标准方程;
的标准方程;
(Ⅱ)若 ,求实数
,求实数 及
及 的值;
的值;
(Ⅲ)当 变化时,求弦长
变化时,求弦长 的取值范围.
的取值范围.
 以点
以点 为圆心,并且经过坐标原点
为圆心,并且经过坐标原点 ,设直线
,设直线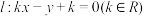 与圆
与圆 相交于
相交于 两点.
两点. (Ⅰ)求圆
 的标准方程;
的标准方程; (Ⅱ)若
 ,求实数
,求实数 及
及 的值;
的值;(Ⅲ)当
 变化时,求弦长
变化时,求弦长 的取值范围.
的取值范围.
您最近一年使用:0次
2019-10-14更新
|
440次组卷
|
3卷引用:四川省宜宾市叙州区第二中学校2022届高三三诊模拟考试文科数学试题
7 . 已知圆 和圆
和圆 的极坐标方程分别为
的极坐标方程分别为 和
和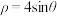 ,曲线
,曲线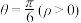 分别交圆
分别交圆 和圆
和圆 于
于 、
、 两点,以极点
两点,以极点 为原点,极轴为
为原点,极轴为 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.
(1)将圆 和圆
和圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)已知点 在圆
在圆 上,求三角形
上,求三角形 面积取最大值时,点
面积取最大值时,点 的直角坐标.
的直角坐标.
 和圆
和圆 的极坐标方程分别为
的极坐标方程分别为 和
和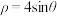 ,曲线
,曲线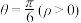 分别交圆
分别交圆 和圆
和圆 于
于 、
、 两点,以极点
两点,以极点 为原点,极轴为
为原点,极轴为 轴正半轴建立直角坐标系.
轴正半轴建立直角坐标系.(1)将圆
 和圆
和圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(2)已知点
 在圆
在圆 上,求三角形
上,求三角形 面积取最大值时,点
面积取最大值时,点 的直角坐标.
的直角坐标.
您最近一年使用:0次
2019-01-01更新
|
824次组卷
|
2卷引用:【市级联考】四川省德阳市2019届高三“一诊”考试数学(文)试题
8 . 选修4-4:坐标系与参数方程
在平面直角坐标系 中,曲线
中,曲线
 (
( 是参数).在以
是参数).在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 :
: .点
.点 是曲线
是曲线 上的动点.
上的动点.
(1)求点 到曲线
到曲线 的距离的最大值;
的距离的最大值;
(2)若曲线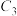 :
: 交曲线
交曲线 于
于 两点,求
两点,求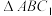 的面积.
的面积.
在平面直角坐标系
 中,曲线
中,曲线
 (
( 是参数).在以
是参数).在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 :
: .点
.点 是曲线
是曲线 上的动点.
上的动点.(1)求点
 到曲线
到曲线 的距离的最大值;
的距离的最大值;(2)若曲线
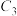 :
: 交曲线
交曲线 于
于 两点,求
两点,求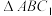 的面积.
的面积.
您最近一年使用:0次
2017-05-04更新
|
749次组卷
|
2卷引用:四川省广元市2017届高三第三次高考适应性统考(三诊)数学(理)试题



