名校
解题方法
1 . 已知双曲线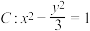 的右焦点与抛物线
的右焦点与抛物线 的焦点重合.
的焦点重合.
(1)求抛物线 的标准方程;
的标准方程;
(2)若过双曲线 的右顶点且斜率为2的直线
的右顶点且斜率为2的直线 与抛物线
与抛物线 交于
交于 ,
, 两点,求线段
两点,求线段 的长度.
的长度.
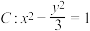 的右焦点与抛物线
的右焦点与抛物线 的焦点重合.
的焦点重合.(1)求抛物线
 的标准方程;
的标准方程;(2)若过双曲线
 的右顶点且斜率为2的直线
的右顶点且斜率为2的直线 与抛物线
与抛物线 交于
交于 ,
, 两点,求线段
两点,求线段 的长度.
的长度.
您最近一年使用:0次
2023-11-19更新
|
705次组卷
|
6卷引用:浙江省嘉兴市第一中学2023-2024学年高二上学期12月阶段测试数学试卷
2 . 已知动点 到直线
到直线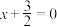 的距离与它到点
的距离与它到点 的距离之差为
的距离之差为
(1)求点 的轨迹方程,并写出焦点坐标和准线方程;
的轨迹方程,并写出焦点坐标和准线方程;
(2)若曲线的准线与 轴的交点为
轴的交点为 ,点
,点 在曲线
在曲线 上,且
上,且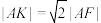 ,求
,求 的面积;
的面积;
(3)若过点 的直线交曲线于
的直线交曲线于 两点,求证:以
两点,求证:以 为直径的圆过原点.
为直径的圆过原点.
 到直线
到直线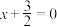 的距离与它到点
的距离与它到点 的距离之差为
的距离之差为
(1)求点
 的轨迹方程,并写出焦点坐标和准线方程;
的轨迹方程,并写出焦点坐标和准线方程;(2)若曲线的准线与
 轴的交点为
轴的交点为 ,点
,点 在曲线
在曲线 上,且
上,且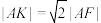 ,求
,求 的面积;
的面积;(3)若过点
 的直线交曲线于
的直线交曲线于 两点,求证:以
两点,求证:以 为直径的圆过原点.
为直径的圆过原点.
您最近一年使用:0次
3 . 倾斜角为 的直线
的直线 过抛物线
过抛物线 的焦点,且与
的焦点,且与 交于A,
交于A, 两点
两点
(1)求抛物线的准线方程;
(2)求 的面积(
的面积( 为坐标原点).
为坐标原点).
 的直线
的直线 过抛物线
过抛物线 的焦点,且与
的焦点,且与 交于A,
交于A, 两点
两点(1)求抛物线的准线方程;
(2)求
 的面积(
的面积( 为坐标原点).
为坐标原点).
您最近一年使用:0次
2023-09-26更新
|
1456次组卷
|
8卷引用:浙江省嘉兴市第五高级中学2022-2023学年高二上学期期中数学试题
浙江省嘉兴市第五高级中学2022-2023学年高二上学期期中数学试题(已下线)考点巩固卷22 抛物线方程及其性质(十大考点)江苏省泰州市靖江高级中学2023-2024学年高二上学期11月期中数学试题福建省福州市福清西山学校2023-2024学年高二上学期12月月考数学试题(已下线)3.3.1 抛物线的标准方程(五大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第一册)(已下线)2023-2024学年高二上学期期中数学模拟试卷(原卷版)(已下线)专题27 抛物线的简单几何性质7种常见考法归类 - 【考点通关】2023-2024学年高二数学高频考点与解题策略(人教A版2019选择性必修第一册)(已下线)通关练17 抛物线8考点精练(2)
解题方法
4 . 已知 、
、 是抛物线
是抛物线 :
: 上的两点,
上的两点, 是线段
是线段 的中点,过点
的中点,过点 和
和 分别作
分别作 的切线
的切线 、
、 ,交于点
,交于点
(1)证明: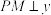 轴:
轴:
(2)若点 的坐标为
的坐标为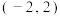 ,求
,求 的面积.
的面积.
注:抛物线 在点
在点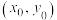 处的切线方程为
处的切线方程为 .
.
 、
、 是抛物线
是抛物线 :
: 上的两点,
上的两点, 是线段
是线段 的中点,过点
的中点,过点 和
和 分别作
分别作 的切线
的切线 、
、 ,交于点
,交于点
(1)证明:
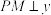 轴:
轴:(2)若点
 的坐标为
的坐标为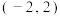 ,求
,求 的面积.
的面积.注:抛物线
 在点
在点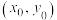 处的切线方程为
处的切线方程为 .
.
您最近一年使用:0次
解题方法
5 . 已知椭圆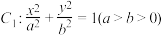 的左、右焦点分别为
的左、右焦点分别为 ,
, ,椭圆
,椭圆 上的点
上的点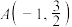 到两焦点
到两焦点 ,
, 的距离之和为4.
的距离之和为4.
(1)求椭圆 的标准方程;
的标准方程;
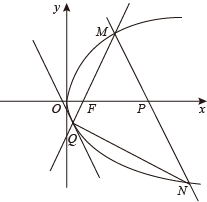
(2)若抛物线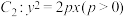 的焦点
的焦点 与椭圆
与椭圆 的右焦点
的右焦点 重合,过点
重合,过点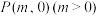 作直线
作直线 交抛物线
交抛物线 于点M,N,直线
于点M,N,直线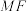 交抛物线
交抛物线 于点Q,以Q为切点作抛物线
于点Q,以Q为切点作抛物线 的切线
的切线 ,且
,且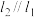 ,求
,求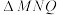 面积S的最小值.
面积S的最小值.
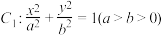 的左、右焦点分别为
的左、右焦点分别为 ,
, ,椭圆
,椭圆 上的点
上的点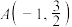 到两焦点
到两焦点 ,
, 的距离之和为4.
的距离之和为4.
(1)求椭圆
 的标准方程;
的标准方程;(2)若抛物线
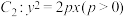 的焦点
的焦点 与椭圆
与椭圆 的右焦点
的右焦点 重合,过点
重合,过点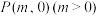 作直线
作直线 交抛物线
交抛物线 于点M,N,直线
于点M,N,直线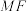 交抛物线
交抛物线 于点Q,以Q为切点作抛物线
于点Q,以Q为切点作抛物线 的切线
的切线 ,且
,且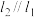 ,求
,求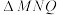 面积S的最小值.
面积S的最小值.
您最近一年使用:0次
6 . 已知斜率为k的直线l经过抛物线 的焦点F,且与抛物线C交
的焦点F,且与抛物线C交 ,
,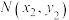 两点,则以下结论正确的是( )
两点,则以下结论正确的是( )
 的焦点F,且与抛物线C交
的焦点F,且与抛物线C交 ,
,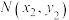 两点,则以下结论正确的是( )
两点,则以下结论正确的是( )A.若 ,则MN的中点到y轴的距离为6 ,则MN的中点到y轴的距离为6 |
B.对任意实数k,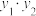 为定值 为定值 |
C.存在实数k,使得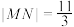 成立 成立 |
D.若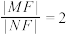 ,则 ,则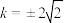 |
您最近一年使用:0次
2022-02-15更新
|
412次组卷
|
3卷引用:浙江省嘉兴市第一中学2023-2024学年高二上学期12月阶段测试数学试卷
名校
解题方法
7 . 过抛物线 :
: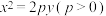 的焦点
的焦点 作两条互相垂直的弦
作两条互相垂直的弦 ,
, ,设
,设 为抛物线上的一动点,
为抛物线上的一动点,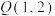 ,若
,若 ,则
,则 的最小值是( )
的最小值是( )
 :
: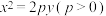 的焦点
的焦点 作两条互相垂直的弦
作两条互相垂直的弦 ,
, ,设
,设 为抛物线上的一动点,
为抛物线上的一动点,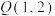 ,若
,若 ,则
,则 的最小值是( )
的最小值是( )| A.2 | B.3 | C.4 | D.5 |
您最近一年使用:0次
2021-12-25更新
|
1058次组卷
|
5卷引用:浙江省平湖市当湖高级中学2022-2023学年高二上学期12月阶段测试数学试题
名校
解题方法
8 . 已知抛物线 :
: ,过点
,过点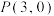 的直线
的直线 交抛物线
交抛物线 于
于 ,
, ,且
,且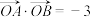 (
( 为坐标原点).
为坐标原点).
(1)求抛物线 的方程;
的方程;
(2)过 作与直线
作与直线 垂直的直线
垂直的直线 交抛物线
交抛物线 于
于 ,
, .求四边形
.求四边形 面积的最小值.
面积的最小值.
 :
: ,过点
,过点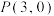 的直线
的直线 交抛物线
交抛物线 于
于 ,
, ,且
,且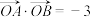 (
( 为坐标原点).
为坐标原点).(1)求抛物线
 的方程;
的方程;(2)过
 作与直线
作与直线 垂直的直线
垂直的直线 交抛物线
交抛物线 于
于 ,
, .求四边形
.求四边形 面积的最小值.
面积的最小值.
您最近一年使用:0次
2021-10-14更新
|
864次组卷
|
8卷引用:浙江省嘉兴一中2021-2022学年高二上学期期中数学试题
浙江省嘉兴一中2021-2022学年高二上学期期中数学试题云南省玉溪市普通高中2022届高三第一次教学质量检测数学(文)试题云南省玉溪市普通高中2022届高三第一次教学质量检测数学(理)试题(已下线)9.6 三定问题及最值(精讲)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)第3.6讲 抛物线的简单几何性质-2021-2022学年高二数学链接教材精准变式练(人教A版2019选择性必修第一册)(已下线)专题32 借用基本不等式解决最值、范围问题-备战2022年高考数学一轮复习一网打尽之重点难点突破(已下线)一轮复习大题专练70—抛物线4(面积最值问题1)—2022届高三数学一轮复习陕西省西安铁一中滨河高级中学2021-2022学年高三上学期学情调查(四)理科数学试题
9 . 如图,已知抛物线 与x轴相交于点A,B两点,P是该抛物线上位于第一象限内的点.
与x轴相交于点A,B两点,P是该抛物线上位于第一象限内的点.
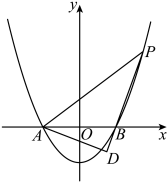
(1)记直线 的斜率分别为
的斜率分别为 ,求证
,求证 为定值;
为定值;
(2)过点A作 ,垂足为D.若D关于x轴的对称点恰好在直线
,垂足为D.若D关于x轴的对称点恰好在直线 上,求
上,求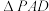 的面积.
的面积.
 与x轴相交于点A,B两点,P是该抛物线上位于第一象限内的点.
与x轴相交于点A,B两点,P是该抛物线上位于第一象限内的点.
(1)记直线
 的斜率分别为
的斜率分别为 ,求证
,求证 为定值;
为定值;(2)过点A作
 ,垂足为D.若D关于x轴的对称点恰好在直线
,垂足为D.若D关于x轴的对称点恰好在直线 上,求
上,求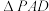 的面积.
的面积.
您最近一年使用:0次
解题方法
10 . 已知点 为抛物线
为抛物线 上的两点,
上的两点, 为坐标原点,且
为坐标原点,且 ,则
,则 的面积的最小值为( )
的面积的最小值为( )
 为抛物线
为抛物线 上的两点,
上的两点, 为坐标原点,且
为坐标原点,且 ,则
,则 的面积的最小值为( )
的面积的最小值为( )| A.8 | B.16 | C.32 | D.64 |
您最近一年使用:0次



