名校
1 . 计算:
(1)已知二项式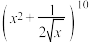 ,求展开式中的第5项和求展开式中的常数项;
,求展开式中的第5项和求展开式中的常数项;
(2)用数学归纳法证明: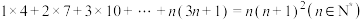 .
.
(1)已知二项式
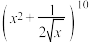 ,求展开式中的第5项和求展开式中的常数项;
,求展开式中的第5项和求展开式中的常数项;(2)用数学归纳法证明:
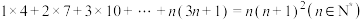 .
.
您最近一年使用:0次
解题方法
2 . 已知函数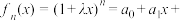
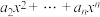 ,其中
,其中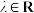 .
.
(1)若 ,
,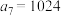 ,求
,求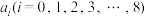 的最大值;
的最大值;
(2)若 ,求证:
,求证: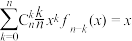 .
.
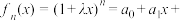
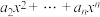 ,其中
,其中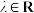 .
.(1)若
 ,
,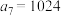 ,求
,求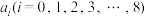 的最大值;
的最大值;(2)若
 ,求证:
,求证: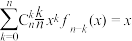 .
.
您最近一年使用:0次
3 . 已知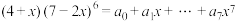 .在以下A,B,C三问中任选两问作答,若三问都分别作答,则按前两问作答计分,作答时,请在答题卷上标明所选两问的题号.
.在以下A,B,C三问中任选两问作答,若三问都分别作答,则按前两问作答计分,作答时,请在答题卷上标明所选两问的题号.
(A)求 ;
;
(B)求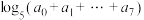 ;
;
(C)设 ,证明:
,证明: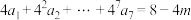 .
.
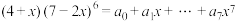 .在以下A,B,C三问中任选两问作答,若三问都分别作答,则按前两问作答计分,作答时,请在答题卷上标明所选两问的题号.
.在以下A,B,C三问中任选两问作答,若三问都分别作答,则按前两问作答计分,作答时,请在答题卷上标明所选两问的题号.(A)求
 ;
;(B)求
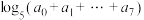 ;
;(C)设
 ,证明:
,证明: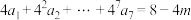 .
.
您最近一年使用:0次
名校
解题方法
4 . 请先阅读:在等式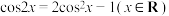 的两边求导,得:
的两边求导,得: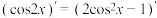 ,由求导法则,得
,由求导法则,得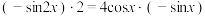 ,化简得等式:
,化简得等式: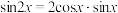 .
.
利用上述的想法,结合等式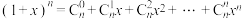 (
( ,正整数
,正整数 ).
).
(1)求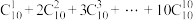 的值.
的值.
(2)求证: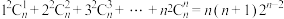 .
.
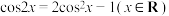 的两边求导,得:
的两边求导,得: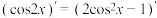 ,由求导法则,得
,由求导法则,得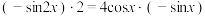 ,化简得等式:
,化简得等式: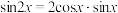 .
.利用上述的想法,结合等式
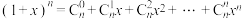 (
( ,正整数
,正整数 ).
).(1)求
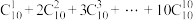 的值.
的值.(2)求证:
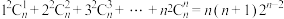 .
.
您最近一年使用:0次
2022-05-14更新
|
378次组卷
|
3卷引用:江苏省南通市重点中学2021-2022学年高二下学期期中数学试题
解题方法
5 . 已知 为偶数,
为偶数,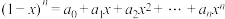 .
.
(1)当 时,求
时,求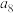 的值;
的值;
(2)证明: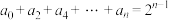 .
.
 为偶数,
为偶数,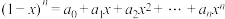 .
.(1)当
 时,求
时,求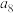 的值;
的值;(2)证明:
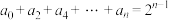 .
.
您最近一年使用:0次
名校
6 . 已知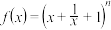 ,
,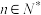 .
.
(1)记 展开式中的常数项为m,当
展开式中的常数项为m,当 时,求m的值;
时,求m的值;
(2)证明:当 时,在
时,在 的展开式中,
的展开式中, 与
与 的系数相同.
的系数相同.
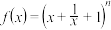 ,
,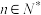 .
.(1)记
 展开式中的常数项为m,当
展开式中的常数项为m,当 时,求m的值;
时,求m的值;(2)证明:当
 时,在
时,在 的展开式中,
的展开式中, 与
与 的系数相同.
的系数相同.
您最近一年使用:0次
2021-10-26更新
|
311次组卷
|
5卷引用:沪教版(2020) 选修第二册 单元训练 第6章 计数原理 二项式定理及其应用(B卷)
名校
解题方法
7 . 在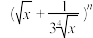 的展开式中,第2,3,4项的二项式系数依次成等差数列.
的展开式中,第2,3,4项的二项式系数依次成等差数列.
(1)证明:展开式中没有常数项;
(2)求展开式中系数最大的项.
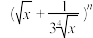 的展开式中,第2,3,4项的二项式系数依次成等差数列.
的展开式中,第2,3,4项的二项式系数依次成等差数列.(1)证明:展开式中没有常数项;
(2)求展开式中系数最大的项.
您最近一年使用:0次
2022-04-30更新
|
436次组卷
|
3卷引用:江苏省宿迁市沭阳县2021-2022学年高二下学期期中数学试题
名校
8 . 已知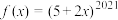 .
.
(1)证明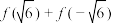 是整数,并求
是整数,并求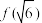 的整数部分的个位数;
的整数部分的个位数;
(2)将 按照
按照 的升幂展开,求展开式中系数最大和最小的项的项数.
的升幂展开,求展开式中系数最大和最小的项的项数.
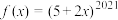 .
.(1)证明
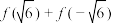 是整数,并求
是整数,并求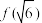 的整数部分的个位数;
的整数部分的个位数;(2)将
 按照
按照 的升幂展开,求展开式中系数最大和最小的项的项数.
的升幂展开,求展开式中系数最大和最小的项的项数.
您最近一年使用:0次
2021-07-12更新
|
691次组卷
|
4卷引用:沪教版(2020) 选修第二册 单元训练 期中测试
20-21高二·江苏·课后作业
名校
9 . 在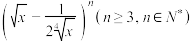 的展开式中,第2,3,4项的二项式系数依次成等差数列.
的展开式中,第2,3,4项的二项式系数依次成等差数列.
(1)证明展开式中没有常数项;
(2)求展开式中所有的有理项.
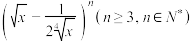 的展开式中,第2,3,4项的二项式系数依次成等差数列.
的展开式中,第2,3,4项的二项式系数依次成等差数列.(1)证明展开式中没有常数项;
(2)求展开式中所有的有理项.
您最近一年使用:0次
2021-12-06更新
|
917次组卷
|
7卷引用:广东省佛山市南海区南海中学2021-2022学年高二下学期第三次大测数学试题
19-20高二下·江苏苏州·期中
10 . 已知函数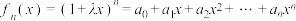 ,其中
,其中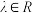 .
.
(1)若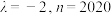 ,求
,求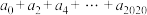 的值;
的值;
(2)若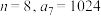 ,求
,求 的最大值;
的最大值;
(3)若 ,求证:
,求证: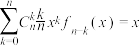 .
.
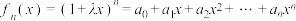 ,其中
,其中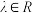 .
.(1)若
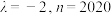 ,求
,求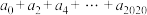 的值;
的值;(2)若
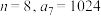 ,求
,求 的最大值;
的最大值;(3)若
 ,求证:
,求证: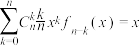 .
.
您最近一年使用:0次



