真题
名校
1 . 集合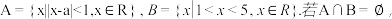 则实数a的取值
则实数a的取值
范围是( )
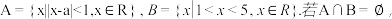 则实数a的取值
则实数a的取值范围是( )
A.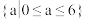 | B.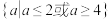 |
C.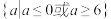 | D.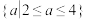 |
您最近一年使用:0次
2016-11-30更新
|
2622次组卷
|
19卷引用:2016届黑龙江省齐齐哈尔市实验中学高三上期中理科数学试卷
2016届黑龙江省齐齐哈尔市实验中学高三上期中理科数学试卷2016届黑龙江省齐齐哈尔市实验中学高三上期中文科数学试卷2010年高考天津(文科)数学试题(已下线)2011届江西省上高二中高三第一次月考理科数学卷(已下线)2014届人教版高考数学文科二轮专题复习提分训练11练习卷(已下线)2014年高考数学考前复习冲刺穿插滚动练习(六)(已下线)2014届天津市天津一中高三上学期第二次月考文科数学试卷(已下线)2015届湖北省浠水实验高中高三上学期期中考试文科数学试卷2017届湖北省沙市中学高三上学期第二次考试理科数学卷陕西省安康市石泉县江南高级中学北师大版高一数学必修一第一章《集合》章节检测题智能测评与辅导[理]-集合的概念与运算四川省棠湖中学2019-2020学年高二上学期开学考试数学(理)试题四川省棠湖中学2019-2020学年高二上学期开学考试数学(文)试题江苏省宿迁市沭阳县2019-2020学年高一上学期期中数学试题贵州省毕节市实验高级中学2020-2021学年高一上学期第一次月考数学试题河南省驻马店市正阳县高级中学2020-2021学年高三预测数学(理)试题沪教版(2020) 必修第一册 领航者 一课一练 第2章 2.2 第6课时 含绝对值不等式的求解(已下线)1.1集合-2【课堂例】2.2.6 含绝对值不等式的求解 课堂例题 沪教版(2020)必修第一册 第2章 等式与不等式
名校
解题方法
2 . 已知函数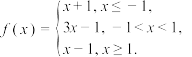
 的图像;
的图像;
(2)求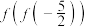 ;
;
(3)求方程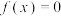 的解集,并说明当整数
的解集,并说明当整数 在何范围时,
在何范围时,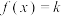 .有且仅有一解.
.有且仅有一解.
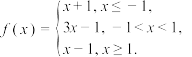

 的图像;
的图像;(2)求
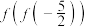 ;
;(3)求方程
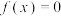 的解集,并说明当整数
的解集,并说明当整数 在何范围时,
在何范围时,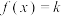 .有且仅有一解.
.有且仅有一解.
您最近一年使用:0次
2023-12-09更新
|
417次组卷
|
12卷引用:黑龙江省齐齐哈尔市克东县第一中学2023-2024学年高一上学期12月月考数学试卷
黑龙江省齐齐哈尔市克东县第一中学2023-2024学年高一上学期12月月考数学试卷黑龙江省鹤岗市第一中学2023-2024学年高一上学期11月月考数学试题贵州省铜仁市第八中学2023-2024学年高一上学期12月月考数学试题内蒙古乌兰浩特市第四中学2023-2024学年高一上学期期中考试数学试题贵州省黔东南苗族侗族自治州锦屏中学2023-2024学年高一上学期期中考试数学试题云南省曲靖市马龙区第一中学2023-2024学年高一上学期期末考试数学试题西藏自治区那曲市五校2023-2024学年高一上学期期末联考数学试题广西壮族自治区崇左市大新县民族高级中学2023-2024学年高一上学期期中考试数学试题新疆维吾尔自治区阜康市第一中学2023-2024学年高一上学期期中考试数学试卷内蒙古集宁新世纪中学2023-2024学年高一上学期期末数学试卷云南省曲靖市第二中学经开区校区2023-2024学年高一上学期期中教学质量检测数学试题陕西省榆林市神木市第四中学2023-2024学年高一上学期第四次检测考试数学试题
名校
3 . 已知函数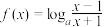 (
( 且
且 ).
).
(1)求 的定义域;
的定义域;
(2)若当 时,函数
时,函数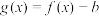 在
在 有且只有一个零点,求实数b的范围;
有且只有一个零点,求实数b的范围;
(3)是否存在实数a,使得当 的定义域为
的定义域为 时,值域为
时,值域为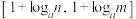 ,若存在,求出实数a的取值范围;若不存在,请说明理由.
,若存在,求出实数a的取值范围;若不存在,请说明理由.
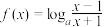 (
( 且
且 ).
).(1)求
 的定义域;
的定义域;(2)若当
 时,函数
时,函数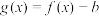 在
在 有且只有一个零点,求实数b的范围;
有且只有一个零点,求实数b的范围;(3)是否存在实数a,使得当
 的定义域为
的定义域为 时,值域为
时,值域为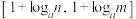 ,若存在,求出实数a的取值范围;若不存在,请说明理由.
,若存在,求出实数a的取值范围;若不存在,请说明理由.
您最近一年使用:0次
2024-02-04更新
|
501次组卷
|
4卷引用:黑龙江省鹤岗市萝北县高级中学2024-2025学年高二上学期开学数学试题
名校
4 . 已知二次函数 满足
满足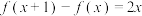 且
且 .
.
(1)求 的解析式;
的解析式;
(2)若方程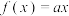 ,
,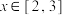 时有唯一一个零点,且不是重根,求
时有唯一一个零点,且不是重根,求 的取值范围;
的取值范围;
(3)当 时,不等式
时,不等式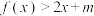 恒成立,求实数
恒成立,求实数 的范围.
的范围.
 满足
满足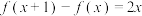 且
且 .
.(1)求
 的解析式;
的解析式;(2)若方程
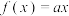 ,
,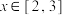 时有唯一一个零点,且不是重根,求
时有唯一一个零点,且不是重根,求 的取值范围;
的取值范围;(3)当
 时,不等式
时,不等式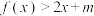 恒成立,求实数
恒成立,求实数 的范围.
的范围.
您最近一年使用:0次
2023-02-22更新
|
491次组卷
|
3卷引用:黑龙江省龙西北高中名校联盟2023-2024学年高三上学期开学考试数学试题
名校
解题方法
5 . 已知函数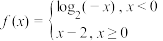 ,若函数
,若函数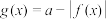 有四个零点
有四个零点 ,
, ,
, ,
, ,且
,且 ,则下列正确的是( )
,则下列正确的是( )
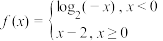 ,若函数
,若函数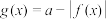 有四个零点
有四个零点 ,
, ,
, ,
, ,且
,且 ,则下列正确的是( )
,则下列正确的是( )A. 的范围 的范围 | B. + + + + + + 的范围 的范围 |
C.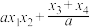 的取值范围 的取值范围  | D. 的范围 的范围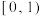 |
您最近一年使用:0次
2023-01-11更新
|
1076次组卷
|
4卷引用:黑龙江省哈尔滨市第九中学校2023-2024学年高一上学期12月月考数学试卷
解题方法
6 . 已知函数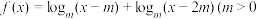 且
且 .
.
(1)若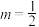 ,求不等式
,求不等式 的解集;
的解集;
(2)若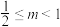 ,是否存在
,是否存在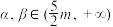 ,使得
,使得 在区间
在区间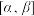 上的值域是
上的值域是 ,若存在,求实数
,若存在,求实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
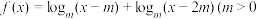 且
且 .
.(1)若
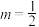 ,求不等式
,求不等式 的解集;
的解集;(2)若
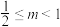 ,是否存在
,是否存在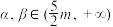 ,使得
,使得 在区间
在区间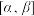 上的值域是
上的值域是 ,若存在,求实数
,若存在,求实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
您最近一年使用:0次
名校
解题方法
7 . 在数学中,双曲函数是与三角函数类似的函数,最基本的双曲函数是双曲正弦函数与双曲余弦函数,其中双曲正弦: 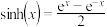 ,双曲余弦:
,双曲余弦: 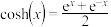 .
.
( 是自然对数的底数,
是自然对数的底数,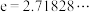 )
)
(1)解方程: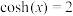 ;
;
(2)求不等式: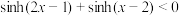 的解集;
的解集;
(3)若对任意的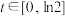 ,关于
,关于 的方程
的方程  有解,求实数
有解,求实数 取值范围.
取值范围.
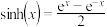 ,双曲余弦:
,双曲余弦: 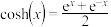 .
.(
 是自然对数的底数,
是自然对数的底数,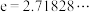 )
)(1)解方程:
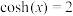 ;
;(2)求不等式:
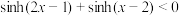 的解集;
的解集;(3)若对任意的
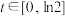 ,关于
,关于 的方程
的方程  有解,求实数
有解,求实数 取值范围.
取值范围.
您最近一年使用:0次
2024-03-19更新
|
213次组卷
|
4卷引用:黑龙江省大庆铁人中学2023-2024学年高一下学期开学考试数学试题
黑龙江省大庆铁人中学2023-2024学年高一下学期开学考试数学试题上海市(进才、复旦附中分校等校)四校联考2023-2024学年高一上学期12月月考数学试卷(已下线)专题04 指数函数与对数函数3-2024年高一数学寒假作业单元合订本2024年贵州省观山湖第一中学高一年级第二学期5月月考数学试题
名校
解题方法
8 . 已知函数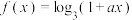 ,
,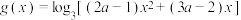 ,
, .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)已知函数 ,且方程
,且方程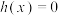 有唯一实数解,求实数
有唯一实数解,求实数 的取值范围.
的取值范围.
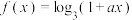 ,
,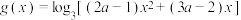 ,
, .
.(1)若
 ,求不等式
,求不等式 的解集;
的解集;(2)已知函数
 ,且方程
,且方程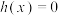 有唯一实数解,求实数
有唯一实数解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2022-11-30更新
|
1337次组卷
|
5卷引用:黑龙江省齐齐哈尔市2020-2021学年高二下学期期末考试数学(文)试题
黑龙江省齐齐哈尔市2020-2021学年高二下学期期末考试数学(文)试题(已下线)专题4.11 指数函数、对数函数的综合应用大题专项训练(30道)-2021-2022学年高一数学举一反三系列(人教A版2019必修第一册)广西桂林市第十八中学2022-2023学年高一上学期期中考试数学试题江苏省宿迁市泗阳县实验高级中学2022-2023学年高一上学期期末数学试题四川省成都市龙泉驿区东竞高级中学2023-2024学年高一上学期12月月考数学试题
名校
解题方法
9 . 已知函数 是定义在
是定义在 上的奇函数.
上的奇函数.
(1)求实数a的值;
(2)求不等式 的解集;
的解集;
(3)若关于x的不等式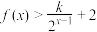 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
 是定义在
是定义在 上的奇函数.
上的奇函数.(1)求实数a的值;
(2)求不等式
 的解集;
的解集;(3)若关于x的不等式
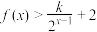 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
您最近一年使用:0次
2022-07-13更新
|
3451次组卷
|
10卷引用:黑龙江省实验中学2022-2023学年高一上学期期中数学试题
黑龙江省实验中学2022-2023学年高一上学期期中数学试题河南省商开大联考2021-2022学年高二下学期期末数学(理)试题(已下线)专题4 指数不等式 (提升版)山西省榆次第一中学校2022-2023学年高二上学期开学考试数学试题第四章 指数函数与对数函数(A卷·基础提升练)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第一册)江西省上饶市、景德镇市六校2023届高三上学期10月联考数学(理)试题广东省东莞实验中学2022-2023学年高一上学期月考二数学试题安徽省安庆市怀宁县新安中学2023-2024学年高一上学期期中考试数学试题内蒙古呼伦贝尔市满洲里远方中学2023-2024学年高一上学期11月月考数学试卷辽宁省沈阳市东北育才中学2024-2025学年高一上学期期中考试数学试题
名校
解题方法
10 . 已知 ,函数
,函数 .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)若方程 的解集恰有一个元素,求
的解集恰有一个元素,求 的取值范围.
的取值范围.
 ,函数
,函数 .
.(1)若
 ,求不等式
,求不等式 的解集;
的解集;(2)若方程
 的解集恰有一个元素,求
的解集恰有一个元素,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-07-29更新
|
350次组卷
|
2卷引用:黑龙江省大庆实验中学2021-2022学年高二实验一部下学期期末考试数学试题



