名校
1 . 已知a∈R,函数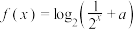 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若关于 的方程
的方程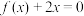 的解集中恰有两个元素,求
的解集中恰有两个元素,求 的取值范围;
的取值范围;
(3)设 ,若对任意
,若对任意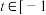 ,
, ,函数
,函数 在区间
在区间 ,
, 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于 ,求
,求 的取值范围.
的取值范围.
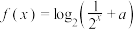 .
.(1)当
 时,解不等式
时,解不等式 ;
;(2)若关于
 的方程
的方程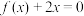 的解集中恰有两个元素,求
的解集中恰有两个元素,求 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意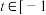 ,
, ,函数
,函数 在区间
在区间 ,
, 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2023-11-30更新
|
509次组卷
|
12卷引用:【校级联考】天津市六校(静海一中、宝坻一中、杨村一中等)2018-2019学年高一上学期期末考试数学试题
【校级联考】天津市六校(静海一中、宝坻一中、杨村一中等)2018-2019学年高一上学期期末考试数学试题河南省信阳市信阳高级中学2021-2022学年高一上学期期末考试理科数学试题河南省信阳市信阳高级中学2021-2022学年高一上学期期末数学文科试题河北省唐山市开滦第二中学2020-2021学年高一上学期期末数学试题广东省新高考2023-2024学年高一上学期期末模拟数学试题辽宁省大连市金普新区2020-2021学年高一下学期开学检测数学试题湖北省部分重点高中2020-2021学年高一下学期四月联考数学试题广西南宁市第三中学(五象校区)2020-2021学年高一下学期期中考试数学试题安徽省合肥市肥东县综合高中2022-2023学年高三上学期10月月考数学试题江西省南昌市八一中学2022-2023学年高一上学期12月月考数学试题(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】(人教A版2019必修第一册)(已下线)对数与对数函数02-一轮复习考点专练
名校
2 . 已知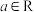 ,函数
,函数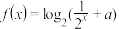 .
.
(Ⅰ)当 时,解不等式
时,解不等式 ;
;
(Ⅱ)若关于 的方程
的方程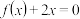 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;
(Ⅲ)设 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于 ,求
,求 的取值范围.
的取值范围.
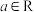 ,函数
,函数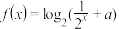 .
.(Ⅰ)当
 时,解不等式
时,解不等式 ;
;(Ⅱ)若关于
 的方程
的方程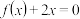 的解集中恰有一个元素,求
的解集中恰有一个元素,求 的取值范围;
的取值范围;(Ⅲ)设
 ,若对任意
,若对任意 ,函数
,函数 在区间
在区间 上的最大值与最小值的和不大于
上的最大值与最小值的和不大于 ,求
,求 的取值范围.
的取值范围.
您最近一年使用:0次
2018-01-26更新
|
1940次组卷
|
2卷引用:天津市新四区示范校2017-2018学年高一上学期期末联考数学试题
名校
解题方法
3 . 设 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.
(1)求函数 在
在 上的解析式;
上的解析式;
(2)解关于 的不等式
的不等式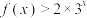 .
.
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.(1)求函数
 在
在 上的解析式;
上的解析式;(2)解关于
 的不等式
的不等式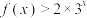 .
.
您最近一年使用:0次
2024-10-09更新
|
426次组卷
|
3卷引用:河北省保定市2022-2023学年高一上学期期末调研考试数学试题
河北省保定市2022-2023学年高一上学期期末调研考试数学试题(已下线)专题2 函数解析式与值域的求法【讲】(高一期中压轴专项)解答题广东省深圳市高级中学2024-2025学年高三上学期第一次诊断测试数学试题
解题方法
4 . 已知函数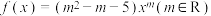 为幂函数,且
为幂函数,且 在
在 上单调递增.
上单调递增.
(1)求m的值,并写出 的解析式;
的解析式;
(2)解关于x的不等式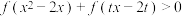 ,其中
,其中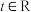 .
.
(3)已知 ,
, ,且
,且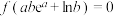 .求
.求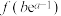 .
.
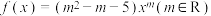 为幂函数,且
为幂函数,且 在
在 上单调递增.
上单调递增.(1)求m的值,并写出
 的解析式;
的解析式;(2)解关于x的不等式
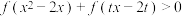 ,其中
,其中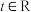 .
.(3)已知
 ,
, ,且
,且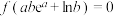 .求
.求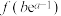 .
.
您最近一年使用:0次
20-21高一·全国·期末
5 . 设函数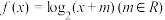 .
.
(1)当 时,解不等式
时,解不等式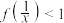 ;
;
(2)若 ,且关于
,且关于 的方程
的方程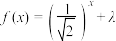 在[-2,6]上有实数解,求实数
在[-2,6]上有实数解,求实数 的取值范围.
的取值范围.
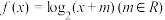 .
.(1)当
 时,解不等式
时,解不等式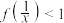 ;
;(2)若
 ,且关于
,且关于 的方程
的方程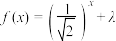 在[-2,6]上有实数解,求实数
在[-2,6]上有实数解,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-09-08更新
|
489次组卷
|
8卷引用:期末复习【真题训练】-2020-2021学年高一数学单元复习(沪教版2020必修第一册)
(已下线)期末复习【真题训练】-2020-2021学年高一数学单元复习(沪教版2020必修第一册)(已下线)期末综合检测一-2021-2022学年高一数学同步单元AB卷(人教A版2019必修第一册)第四章 幂函数、指数函数与对数函数【真题训练】-2020-2021学年高一数学单元复习(沪教版2020必修第一册)江苏省无锡第六高级中学2022届高三10月质量调研数学试题第八章 函数应用(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(苏教版2019必修第一册)(已下线)4.5函数的应用(二)-2021-2022学年高一数学同步辅导讲义与检测(人教A版2019必修第一册)(已下线)第07节 函数的图象与方程(好题帮)-备战2023年高考数学一轮复习考点帮(全国通用)【巩固卷】第5章 函数的概念、性质及应用 单元测试B-沪教版(2020)必修一
解题方法
6 . 已知函数 .若当点
.若当点 在函数
在函数 图象上运动时,对应的点
图象上运动时,对应的点 在函数
在函数 图象上运动,则称函数
图象上运动,则称函数 是函数
是函数 的“伴随”函数.
的“伴随”函数.
(1)解关于x的不等式 ;
;
(2)若对任意的 ,
, 的图象总在其“伴随”函数图象的下方,求a的取值范围;
的图象总在其“伴随”函数图象的下方,求a的取值范围;
(3)设函数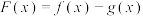 ,
, .当
.当 时,求
时,求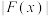 的最大值.
的最大值.
 .若当点
.若当点 在函数
在函数 图象上运动时,对应的点
图象上运动时,对应的点 在函数
在函数 图象上运动,则称函数
图象上运动,则称函数 是函数
是函数 的“伴随”函数.
的“伴随”函数.(1)解关于x的不等式
 ;
;(2)若对任意的
 ,
, 的图象总在其“伴随”函数图象的下方,求a的取值范围;
的图象总在其“伴随”函数图象的下方,求a的取值范围;(3)设函数
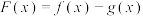 ,
, .当
.当 时,求
时,求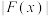 的最大值.
的最大值.
您最近一年使用:0次
解题方法
7 . 已知函数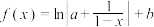 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)证明:函数 在
在 上是增函数;
上是增函数;
(3)解关于 的不等式
的不等式 .
.
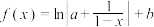 是奇函数.
是奇函数.(1)求
 的值;
的值;(2)证明:函数
 在
在 上是增函数;
上是增函数;(3)解关于
 的不等式
的不等式 .
.
您最近一年使用:0次
名校
解题方法
8 . 已知函数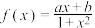 是定义在
是定义在 上的奇函数,且
上的奇函数,且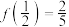 .
.
(1)求函数 的解析式;
的解析式;
(2)判断函数 在
在 上的单调性并用定义证明;
上的单调性并用定义证明;
(3)解关于 的不等式
的不等式 .
.
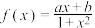 是定义在
是定义在 上的奇函数,且
上的奇函数,且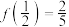 .
.(1)求函数
 的解析式;
的解析式;(2)判断函数
 在
在 上的单调性并用定义证明;
上的单调性并用定义证明;(3)解关于
 的不等式
的不等式 .
.
您最近一年使用:0次
2024-03-19更新
|
1069次组卷
|
7卷引用:河南省三门峡市渑池县第二高级中学2023-2024学年高二下学期7月期末考试数学试题
名校
解题方法
9 . 已知函数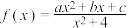 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求函数 的解析式;
的解析式;
(2)判断并用定义法证明 在
在 上的单调性;
上的单调性;
(3)解关于x的不等式 .
.
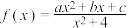 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.(1)求函数
 的解析式;
的解析式;(2)判断并用定义法证明
 在
在 上的单调性;
上的单调性;(3)解关于x的不等式
 .
.
您最近一年使用:0次
2024-06-01更新
|
1683次组卷
|
8卷引用:福建省福州市福建师范大学附属中学2023-2024学年高二下学期7月期末考试数学试题
福建省福州市福建师范大学附属中学2023-2024学年高二下学期7月期末考试数学试题山东省淄博第一中学特殊禀赋班2023-2024学年高一下学期期中检测数学试卷(已下线)第5章 函数概念与性质综合测试-【暑假自学课】(苏教版2019必修第一册)(已下线)第15讲 函数的奇偶性(2)-【暑假自学课】(苏教版2019必修第一册)(已下线)【高二模块二】类型5 以函数为背景的解答题(B卷提升卷)(已下线)第12讲 函数的奇偶性-【暑假自学课】(人教B版2019必修第一册)(已下线)2.2 函数的单调性与最值(高三一轮)【讲】 (提升版)(已下线)2.2函数的单调性与最值【讲】(北京专版)
解题方法
10 . 已知函数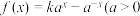 且
且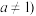 是奇函数,且
是奇函数,且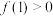 .
.
(1)求实数 的值;
的值;
(2)判断函数 的单调性,并用函数单调性的定义加以证明;
的单调性,并用函数单调性的定义加以证明;
(3)求不等式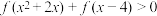 的解.
的解.
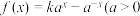 且
且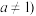 是奇函数,且
是奇函数,且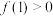 .
.(1)求实数
 的值;
的值;(2)判断函数
 的单调性,并用函数单调性的定义加以证明;
的单调性,并用函数单调性的定义加以证明;(3)求不等式
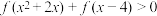 的解.
的解.
您最近一年使用:0次



