名校
解题方法
1 . 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分布在 ,
,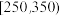 ,
,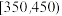 ,
,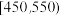 ,
,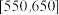 (单位:克)中,经统计频率分布直方图如图所示.
(单位:克)中,经统计频率分布直方图如图所示.
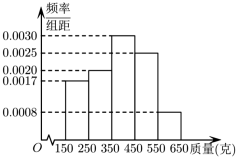
(1)估计这组数据的平均数;
(2)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中共有芒果大约10000个,经销商提出以下两种收购方案:
方案①:所有芒果以10元/千克收购;
方案②:对质量低于350克的芒果以3元/个收购,对质量高于或等于350克的芒果以5元/个收购.
请通过计算确定种植园选择哪种方案获利更多?
 ,
,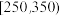 ,
,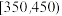 ,
,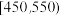 ,
,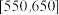 (单位:克)中,经统计频率分布直方图如图所示.
(单位:克)中,经统计频率分布直方图如图所示.
(1)估计这组数据的平均数;
(2)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中共有芒果大约10000个,经销商提出以下两种收购方案:
方案①:所有芒果以10元/千克收购;
方案②:对质量低于350克的芒果以3元/个收购,对质量高于或等于350克的芒果以5元/个收购.
请通过计算确定种植园选择哪种方案获利更多?
您最近一年使用:0次
2022-05-14更新
|
967次组卷
|
7卷引用:广东省惠州市实验中学2023-2024学年高二上学期10月月考数学试题
解题方法
2 . 梅州市沙田柚根据色泽、果面、风味等评分指标打分,得分在区间(0,25],(25,50],(50,75],(75,100]内分别评定为三级柚、二级柚、一级柚,特级柚,某经销商从我市柚农手中收购一批沙田柚,共M袋(每袋50kg),并随机抽取20袋分别进行检测评级,得分数据的频率分布直方图如图所示:

(1)求a的值,并用样本估计该经销商采购的这批沙田柚的平均得分;
(2)该经销商计划在下面两个方案中选择一个作为销售方案:
方案1:将采购的这批沙田柚不经检测,统一按每袋350元直接售出;
方案2:将采购的这批沙田柚逐袋检测分级,并将每袋沙田柚重新包装成5小袋(每小袋10kg),检测分级所需费用和人工费平均每袋20元,各等级沙田柚每小袋的售价和包装材料成本如下表所示:
假设这批沙田柚各级比例按前面随机抽取的20袋的样本结果估计,并可以全部销售出去,那么该经销商采用哪种销售方案所得利润更大?请通过计算说明理由.

(1)求a的值,并用样本估计该经销商采购的这批沙田柚的平均得分;
(2)该经销商计划在下面两个方案中选择一个作为销售方案:
方案1:将采购的这批沙田柚不经检测,统一按每袋350元直接售出;
方案2:将采购的这批沙田柚逐袋检测分级,并将每袋沙田柚重新包装成5小袋(每小袋10kg),检测分级所需费用和人工费平均每袋20元,各等级沙田柚每小袋的售价和包装材料成本如下表所示:
| 沙田柚等级 | 三级 | 二级 | 一级 | 特级 |
| 售价(元/小袋) | 55 | 68 | 85 | 98 |
| 包装材料成本(元/小装) | 2 | 2 | 4 | 5 |
您最近一年使用:0次
名校
3 . 中国北京世界园艺博览会于2019年4月29日至10月7日在北京市延庆区举行.组委会为方便游客游园,特推出“导引员”服务.“导引员”的日工资方案如下:
 方案:由三部分组成
方案:由三部分组成
(表一)
 方案:由两部分组成:(1)根据工作时间20元/小时计费;(2)行走路程不超过4公里时,按10元/公里计费;超过4公里时,超出部分按15元/公里计费.已知“导引员”每天上班8小时,由于各种因素,“导引员”每天行走的路程是一个随机变量.试运行期间,组委会对某天100名“导引员”的行走路程述行了统计,为了计算方便对日行走路程进行取整处理.例如行走1.8公里按1公里计算,行走5.7公里按5公里计算.如表所示:
方案:由两部分组成:(1)根据工作时间20元/小时计费;(2)行走路程不超过4公里时,按10元/公里计费;超过4公里时,超出部分按15元/公里计费.已知“导引员”每天上班8小时,由于各种因素,“导引员”每天行走的路程是一个随机变量.试运行期间,组委会对某天100名“导引员”的行走路程述行了统计,为了计算方便对日行走路程进行取整处理.例如行走1.8公里按1公里计算,行走5.7公里按5公里计算.如表所示:
(表二)
(Ⅰ)分别写出两种方案的日工资 (单位:元)与日行走路程
(单位:元)与日行走路程 (单位:公里)
(单位:公里) 的函数关系
的函数关系
(Ⅱ)①现按照分层抽样的方工式从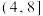 ,
,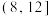 共抽取5人组成爱心服务队,再从这5人中抽取3人当小红帽,求小红帽中恰有1人来自
共抽取5人组成爱心服务队,再从这5人中抽取3人当小红帽,求小红帽中恰有1人来自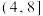 的概率;
的概率;
②“导引员”小张因为身体原因每天只能行走12公里,如果仅从日工资的角度考虑,请你帮小张选择使用哪种方案会使他的日工资更高?
 方案:由三部分组成
方案:由三部分组成(表一)
| 底薪 | 150元 |
| 工作时间 | 6元/小时 |
| 行走路程 | 11元/公里 |
 方案:由两部分组成:(1)根据工作时间20元/小时计费;(2)行走路程不超过4公里时,按10元/公里计费;超过4公里时,超出部分按15元/公里计费.已知“导引员”每天上班8小时,由于各种因素,“导引员”每天行走的路程是一个随机变量.试运行期间,组委会对某天100名“导引员”的行走路程述行了统计,为了计算方便对日行走路程进行取整处理.例如行走1.8公里按1公里计算,行走5.7公里按5公里计算.如表所示:
方案:由两部分组成:(1)根据工作时间20元/小时计费;(2)行走路程不超过4公里时,按10元/公里计费;超过4公里时,超出部分按15元/公里计费.已知“导引员”每天上班8小时,由于各种因素,“导引员”每天行走的路程是一个随机变量.试运行期间,组委会对某天100名“导引员”的行走路程述行了统计,为了计算方便对日行走路程进行取整处理.例如行走1.8公里按1公里计算,行走5.7公里按5公里计算.如表所示:(表二)
| 行走路程 (公里) | 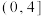 | 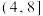 | 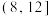 | 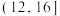 |  |
| 人数 | 5 | 10 | 15 | 45 | 25 |
 (单位:元)与日行走路程
(单位:元)与日行走路程 (单位:公里)
(单位:公里) 的函数关系
的函数关系(Ⅱ)①现按照分层抽样的方工式从
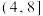 ,
,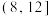 共抽取5人组成爱心服务队,再从这5人中抽取3人当小红帽,求小红帽中恰有1人来自
共抽取5人组成爱心服务队,再从这5人中抽取3人当小红帽,求小红帽中恰有1人来自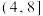 的概率;
的概率;②“导引员”小张因为身体原因每天只能行走12公里,如果仅从日工资的角度考虑,请你帮小张选择使用哪种方案会使他的日工资更高?
您最近一年使用:0次
2020-03-15更新
|
280次组卷
|
2卷引用:广东省惠州大亚湾经济技术开发区第一中学2023-2024学年高二上学期第一次月考数学试题
名校
4 . 从某商场随机抽取了2000件商品,按商品价格(元)进行统计,所得频率分布直方图如图所示.记价格在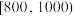 ,
,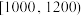 ,
,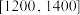 对应的小矩形的面积分别为
对应的小矩形的面积分别为 ,且
,且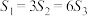 .
.

(1)按分层抽样从价格在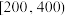 ,
,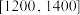 的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
(2)在清明节期间,该商场制定了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表,如果你是消费者,你会选择哪种方案?为什么?(同一组中的数据用该组区间中点值作代表)
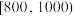 ,
,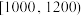 ,
,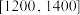 对应的小矩形的面积分别为
对应的小矩形的面积分别为 ,且
,且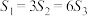 .
.
(1)按分层抽样从价格在
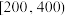 ,
,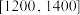 的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;
的商品中共抽取6件,再从这6件中随机抽取2件作价格对比,求抽到的两件商品价格差超过800元的概率;(2)在清明节期间,该商场制定了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表,如果你是消费者,你会选择哪种方案?为什么?(同一组中的数据用该组区间中点值作代表)
| 商品价格 | 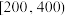 | 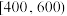 | 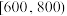 | 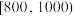 | 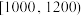 | 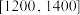 |
| 优惠(元) | 30 | 50 | 140 | 160 | 280 | 320 |
您最近一年使用:0次
2020-02-24更新
|
254次组卷
|
3卷引用:广东省汕头市潮阳区棉城中学2021-2022学年高二上学期期中数学试题
广东省汕头市潮阳区棉城中学2021-2022学年高二上学期期中数学试题重庆市巴蜀中学2018-2019学年高二下学期第一次月考(文)数学试题(已下线)第七章 §2 第1课时 古典概型的概率计算公式及其应用-【新教材】北师大版(2019)高中数学必修第一册练习
5 . 某玻璃工艺品加工厂有2条生产线用于生产其款产品,每条生产线一天能生产200件该产品,该产品市场评级规定:评分在10分及以上的为 等品,低于10分的为
等品,低于10分的为 等品.厂家将
等品.厂家将 等品售价定为2000元/件,
等品售价定为2000元/件, 等品售价定为1200元/件.
等品售价定为1200元/件.
下面是检验员在现有生产线上随机抽取的16件产品的评分:
经计算得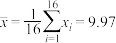 ,
,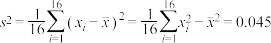 ,其中
,其中 为抽取的第
为抽取的第 件产品的评分,
件产品的评分,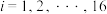 .
.
该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费1500万元,改进后该条生产线产能不变,但生产出的每件产品评分均提高0.05.已知该厂现有一笔1500万元的资金.
(1)若厂家用这1500万元改进一条生产线,根据随机抽取的16件产品的评分.
(i)估计改进后该生产线生产的产品中 等品所占的比例;
等品所占的比例;
(ii)估计改进后该厂生产的所有产品评分的平均数和方差.
(2)某金融机构向该厂推销一款年收益率为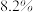 的理财产品,请你利用所学知识分析,将这1500万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大? (一年按365天计算)
的理财产品,请你利用所学知识分析,将这1500万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大? (一年按365天计算)
 等品,低于10分的为
等品,低于10分的为 等品.厂家将
等品.厂家将 等品售价定为2000元/件,
等品售价定为2000元/件, 等品售价定为1200元/件.
等品售价定为1200元/件.下面是检验员在现有生产线上随机抽取的16件产品的评分:
| 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
| 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得
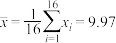 ,
,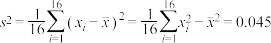 ,其中
,其中 为抽取的第
为抽取的第 件产品的评分,
件产品的评分,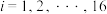 .
.该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费1500万元,改进后该条生产线产能不变,但生产出的每件产品评分均提高0.05.已知该厂现有一笔1500万元的资金.
(1)若厂家用这1500万元改进一条生产线,根据随机抽取的16件产品的评分.
(i)估计改进后该生产线生产的产品中
 等品所占的比例;
等品所占的比例;(ii)估计改进后该厂生产的所有产品评分的平均数和方差.
(2)某金融机构向该厂推销一款年收益率为
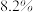 的理财产品,请你利用所学知识分析,将这1500万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大? (一年按365天计算)
的理财产品,请你利用所学知识分析,将这1500万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大? (一年按365天计算)
您最近一年使用:0次
2020-08-03更新
|
938次组卷
|
4卷引用:广东省珠海市大湾区2023-2024学年高二上学期1月期末联合考试数学试题
名校
解题方法
6 . 某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人5次数学考试的成绩,统计结果如下表:
(Ⅰ)已知甲、乙两名学生这5次数学考试成绩的平均分都为83分,若从甲、乙两名学生中选一人参加数学竞赛,请从统计学的角度考虑,你认为选谁参加数学竞赛较合适?并说明理由;
(Ⅱ)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰.方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.已知学生甲、乙都只会5道备选题中的3道,那么你推荐的选手选择哪种答题方案进入复赛的可能性更大?并说明理由.
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| 甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
| 乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(Ⅰ)已知甲、乙两名学生这5次数学考试成绩的平均分都为83分,若从甲、乙两名学生中选一人参加数学竞赛,请从统计学的角度考虑,你认为选谁参加数学竞赛较合适?并说明理由;
(Ⅱ)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:方案一:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰.方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.已知学生甲、乙都只会5道备选题中的3道,那么你推荐的选手选择哪种答题方案进入复赛的可能性更大?并说明理由.
您最近一年使用:0次
2020-08-16更新
|
571次组卷
|
6卷引用:广东省培正中学2021-2022学年高二上学期开学考数学试题
广东省培正中学2021-2022学年高二上学期开学考数学试题陕西省咸阳市2019-2020学年高一下学期期末数学试题(已下线)专题10.3频率与概率单元测试(B卷提升篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版,浙江专用)(已下线)10.3 频率与概率广西百色市2021-2022学年高一下学期期末教学质量调研测试数学试题(已下线)10.3 频率与概率(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)
7 . 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在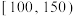 ,
,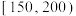 ,
,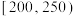 ,
, ,
,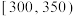 ,
,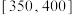 (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.
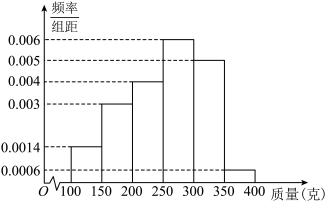
(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据: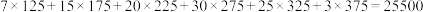 .
.
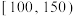 ,
,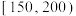 ,
,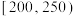 ,
, ,
,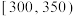 ,
,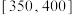 (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.
(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据:
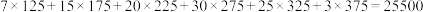 .
.
您最近一年使用:0次
2019-09-23更新
|
601次组卷
|
3卷引用:广东省韶关市2018-2019学年高一第二学期末检测数学试题
名校
8 . 某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在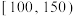 ,
,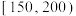 ,
,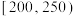 ,
, ,
,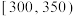 ,
,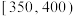 (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为 ,
,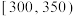 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在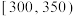 内的概率.
内的概率.
(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
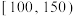 ,
,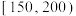 ,
,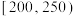 ,
, ,
,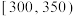 ,
,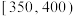 (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1)经计算估计这组数据的中位数;
(2)现按分层抽样从质量为
 ,
,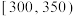 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在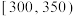 内的概率.
内的概率.(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
A:所有芒果以10元/千克收购;
B:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购,通过计算确定种植园选择哪种方案获利更多?
您最近一年使用:0次
2020-01-10更新
|
1303次组卷
|
17卷引用:【市级联考】广东省潮州市2019届高三上学期期末教学质量检测数学(文)试题
【市级联考】广东省潮州市2019届高三上学期期末教学质量检测数学(文)试题吉林省长春市普通高中2018届高三质量监测(二)数学(文)试题【全国市级联考】陕西省延安市2018届高三高考模拟文科数学试题【全国百强校】郑州外国语学校2018届高三第十五次调研考试(文)试题【市级联考】吉林省长春市2018届高三高考二模数学试题(文科)【市级联考】辽宁省沈阳市郊联体2019届高三第一次模拟考试数学(理科)试题【全国百强校】河北省唐山市第一中学2019届高三下学期冲刺(二)数学(文)试题辽宁省沈阳市郊联体2018-2019学年高一下学期期末数学试题河北省保定七校2019-2020学年高三上学期第三次联考文数试题山西省长治市2019届高三下学期3月统一联合考试数学(文)试题2020届吉林省白城四中高三网上模拟考数学文科试题2020届甘肃省天水市第一中学高三下学期诊断考试数学(文)试题陕西省西安中学2021届高三下学期第四次模拟数学(文)试题(已下线)福建省厦门市集美中学2020-2021学年高一下学期期末数学试题河北省尚义县第一中学2020-2021学年高二下学期期中数学试题黑龙江省大庆铁人中学2021-2022学年高二下学期第一次月考数学试题湖南省长沙市宁乡市2021-2022学年高二下学期期末数学试题
名校
9 . 某省实行“ ”高考模式,为让学生适应新高考的赋分模式,某校在一次校考中使用赋分制给高三年级学生的生物成绩进行赋分,具体赋分方案如下:先按照考生原始分从高到低按比例划定
”高考模式,为让学生适应新高考的赋分模式,某校在一次校考中使用赋分制给高三年级学生的生物成绩进行赋分,具体赋分方案如下:先按照考生原始分从高到低按比例划定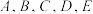 共五个等级,然后在相应赋分区间内利用转换公式进行赋分.其中,
共五个等级,然后在相应赋分区间内利用转换公式进行赋分.其中, 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比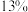 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是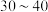 ;现从全年级的生物成绩中随机抽取
;现从全年级的生物成绩中随机抽取 名学生的原始成绩(未赋分)进行分析,其频率分布直方图如下图:
名学生的原始成绩(未赋分)进行分析,其频率分布直方图如下图:
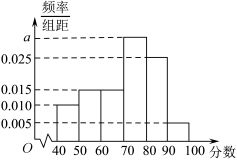
(1)求图中 的值;
的值;
(2)从生物原始成绩为 的学生中用分层抽样的方法抽取
的学生中用分层抽样的方法抽取 人,从这
人,从这 人中任意抽取
人中任意抽取 人,求
人,求 人均在
人均在 的概率;
的概率;
(3)用样本估计总体的方法,估计该校本次生物成绩原始分不少于多少分才能达到赋分后的 等级及以上(含
等级及以上(含 等级)?(结果保留整数)
等级)?(结果保留整数)
 ”高考模式,为让学生适应新高考的赋分模式,某校在一次校考中使用赋分制给高三年级学生的生物成绩进行赋分,具体赋分方案如下:先按照考生原始分从高到低按比例划定
”高考模式,为让学生适应新高考的赋分模式,某校在一次校考中使用赋分制给高三年级学生的生物成绩进行赋分,具体赋分方案如下:先按照考生原始分从高到低按比例划定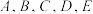 共五个等级,然后在相应赋分区间内利用转换公式进行赋分.其中,
共五个等级,然后在相应赋分区间内利用转换公式进行赋分.其中, 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比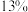 ,赋分分数区间是
,赋分分数区间是 ;
; 等级排名占比
等级排名占比 ,赋分分数区间是
,赋分分数区间是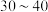 ;现从全年级的生物成绩中随机抽取
;现从全年级的生物成绩中随机抽取 名学生的原始成绩(未赋分)进行分析,其频率分布直方图如下图:
名学生的原始成绩(未赋分)进行分析,其频率分布直方图如下图:
(1)求图中
 的值;
的值;(2)从生物原始成绩为
 的学生中用分层抽样的方法抽取
的学生中用分层抽样的方法抽取 人,从这
人,从这 人中任意抽取
人中任意抽取 人,求
人,求 人均在
人均在 的概率;
的概率;(3)用样本估计总体的方法,估计该校本次生物成绩原始分不少于多少分才能达到赋分后的
 等级及以上(含
等级及以上(含 等级)?(结果保留整数)
等级)?(结果保留整数)
您最近一年使用:0次
2023-07-05更新
|
323次组卷
|
3卷引用:广东省广州市番禺区2022-2023学年高一下学期期末数学试题
名校
解题方法
10 . 为响应十九大报告中提出的“绿水青山就是金山银山”的号召,某市旅游局投入若干经费对全市各旅游景区的环境进行综合治理,并且对各旅游景区收益的增加值作了初步的估计.根据旅游局的治理规划方案,收集了各旅游景区在治理后收益的增加值,将所有数据按照[0,2),[2,4),…,[10,12)分成6组,绘制出如下频率分布直方图.
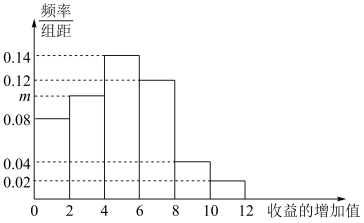
(1)求图中m的值;
(2)利用频率分布直方图估算全市旅游景区收益增加值的平均数 (以各组的区间中点值代表该组的取值);
(以各组的区间中点值代表该组的取值);
(3)若该市旅游局打算奖励收益增加值前10%的旅游景区,需要制定一个标准t万元(即收益增加值大于t则奖励)估计t的值,并说明理由.

(1)求图中m的值;
(2)利用频率分布直方图估算全市旅游景区收益增加值的平均数
 (以各组的区间中点值代表该组的取值);
(以各组的区间中点值代表该组的取值);(3)若该市旅游局打算奖励收益增加值前10%的旅游景区,需要制定一个标准t万元(即收益增加值大于t则奖励)估计t的值,并说明理由.
您最近一年使用:0次
2022-06-03更新
|
713次组卷
|
5卷引用:广东省广州市执信中学2021-2022学年高一下学期5月月考数学试题
广东省广州市执信中学2021-2022学年高一下学期5月月考数学试题广东省东莞市东莞高级中学2022-2023学年高一下学期期中数学试题(已下线)第04讲 用样本估计总体(主干知识复习)-【暑假自学课】2022年新高二数学暑假精品课(人教版2019必修二)(已下线)第10练 统计-2022年【暑假分层作业】高一数学(苏教版2019必修第二册)西藏拉萨市高中六校2021-2022学年高一下学期期末联考数学试题



