名校
1 . 有如下条件:
①对 ,
, ,2,
,2, ,均有
,均有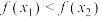 ;
;
②对 ,
, ,2,
,2, ,均有
,均有 ;
;
③对 ,
, ,2,3,
,2,3, ;若
;若 ,则均有
,则均有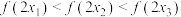 ;
;
④对 ,
, ,2,3,
,2,3, ;若
;若 ,则均有
,则均有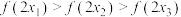 .
.
(1)设函数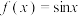 ,
,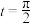 ,请写出该函数满足的所有条件序号,并充分说明理由;
,请写出该函数满足的所有条件序号,并充分说明理由;
(2)设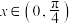 ,比较函数
,比较函数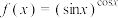 ,
,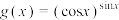 ,
,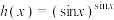 值的大小,并说明理由;
值的大小,并说明理由;
(3)设函数 ,满足条件②,求证:
,满足条件②,求证: 的最大值
的最大值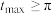 .(注:导数法不予计分)
.(注:导数法不予计分)
①对
 ,
, ,2,
,2, ,均有
,均有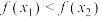 ;
;②对
 ,
, ,2,
,2, ,均有
,均有 ;
;③对
 ,
, ,2,3,
,2,3, ;若
;若 ,则均有
,则均有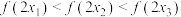 ;
;④对
 ,
, ,2,3,
,2,3, ;若
;若 ,则均有
,则均有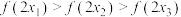 .
.(1)设函数
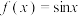 ,
,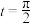 ,请写出该函数满足的所有条件序号,并充分说明理由;
,请写出该函数满足的所有条件序号,并充分说明理由;(2)设
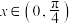 ,比较函数
,比较函数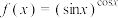 ,
,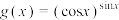 ,
,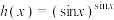 值的大小,并说明理由;
值的大小,并说明理由;(3)设函数
 ,满足条件②,求证:
,满足条件②,求证: 的最大值
的最大值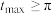 .(注:导数法不予计分)
.(注:导数法不予计分)
您最近一年使用:0次
2024-02-23更新
|
678次组卷
|
5卷引用:河南省驻马店市新蔡县第一高级中学2023-2024学年高一下学期3月月考数学试题
2 . (1)在 中,点
中,点 在
在 边上且
边上且 ,以向量
,以向量 ,
,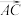 为基底,表示向量
为基底,表示向量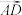 .
.
(2)已知空间向量 ,且
,且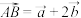 ,
, ,
,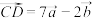 ,求证:A、B、D三点共线.
,求证:A、B、D三点共线.
您最近一年使用:0次
3 . 已知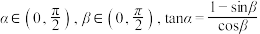 .
.
(1)求证: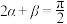 ;
;
(2)若关于 的方程
的方程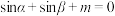 有两个不相等的实根,求实数
有两个不相等的实根,求实数 的取值范围.
的取值范围.
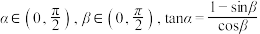 .
.(1)求证:
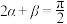 ;
;(2)若关于
 的方程
的方程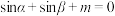 有两个不相等的实根,求实数
有两个不相等的实根,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
名校
4 . 给定平面上一个图形D,以及图形D上的点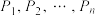 ,如果对于D上任意的点P,
,如果对于D上任意的点P,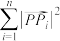 为与P无关的定值,我们就称
为与P无关的定值,我们就称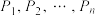 为关于图形D的一组稳定向量基点.
为关于图形D的一组稳定向量基点.
(1)已知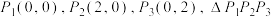 为图形D,判断点
为图形D,判断点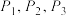 是不是关于图形D的一组稳定向量基点;
是不是关于图形D的一组稳定向量基点;
(2)若图形D是边长为2的正方形,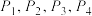 是它的4个顶点,P为该正方形上的动点,求
是它的4个顶点,P为该正方形上的动点,求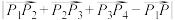 的取值范围;
的取值范围;
(3)若给定单位圆 及其内接正2024边形
及其内接正2024边形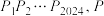 为该单位圆上的任意一点,证明
为该单位圆上的任意一点,证明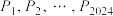 是关于圆
是关于圆 的一组稳定向量基点,并求
的一组稳定向量基点,并求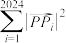 的值.
的值.
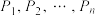 ,如果对于D上任意的点P,
,如果对于D上任意的点P,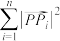 为与P无关的定值,我们就称
为与P无关的定值,我们就称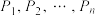 为关于图形D的一组稳定向量基点.
为关于图形D的一组稳定向量基点.(1)已知
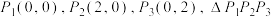 为图形D,判断点
为图形D,判断点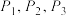 是不是关于图形D的一组稳定向量基点;
是不是关于图形D的一组稳定向量基点;(2)若图形D是边长为2的正方形,
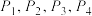 是它的4个顶点,P为该正方形上的动点,求
是它的4个顶点,P为该正方形上的动点,求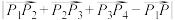 的取值范围;
的取值范围;(3)若给定单位圆
 及其内接正2024边形
及其内接正2024边形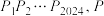 为该单位圆上的任意一点,证明
为该单位圆上的任意一点,证明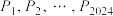 是关于圆
是关于圆 的一组稳定向量基点,并求
的一组稳定向量基点,并求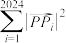 的值.
的值.
您最近一年使用:0次
2024-09-07更新
|
298次组卷
|
3卷引用:河南省驻马店市新蔡县第一高级中学2025届高三上学期9月月考数学试题
河南省驻马店市新蔡县第一高级中学2025届高三上学期9月月考数学试题河北省保定市部分高中2024-2025学年高二上学期开学考试数学试题(已下线)考点30 平面向量与多学科交汇问题 --高考数学100个黄金考点(2025届)【讲】
名校
5 . 对于三维向量 ,定义“
,定义“ 变换”:
变换”: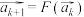 ,其中,
,其中, .记
.记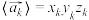 ,
,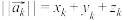 .
.
(1)若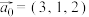 ,求
,求 及
及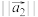 ;
;
(2)证明:对于任意 ,经过若干次
,经过若干次 变换后,必存在
变换后,必存在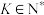 ,使
,使 ;
;
(3)已知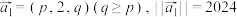 ,将
,将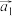 再经过
再经过 次
次 变换后,
变换后,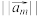 最小,求
最小,求 的最小值.
的最小值.
 ,定义“
,定义“ 变换”:
变换”: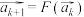 ,其中,
,其中, .记
.记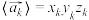 ,
,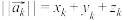 .
.(1)若
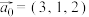 ,求
,求 及
及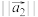 ;
;(2)证明:对于任意
 ,经过若干次
,经过若干次 变换后,必存在
变换后,必存在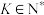 ,使
,使 ;
;(3)已知
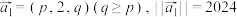 ,将
,将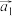 再经过
再经过 次
次 变换后,
变换后,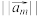 最小,求
最小,求 的最小值.
的最小值.
您最近一年使用:0次
2023-07-11更新
|
1843次组卷
|
8卷引用:河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期8月开学考试数学试题
河南省驻马店市新蔡县第一高级中学2024-2025学年高二上学期8月开学考试数学试题北京市东城区2022-2023学年高一下学期期末统一检测数学试题北京市第十一中学2023-2024学年高二上学期期中练习数学试题广东省东莞市石竹实验学校2023-2024学年高一下学期3月月考数学试卷(已下线)专题02 高一下期末真题精选(1)-期末考点大串讲(人教A版2019必修第二册)【北京专用】专题07平面向量(第三部分)-高一下学期名校期末好题汇编(已下线)专题08 期末必刷解答题专题训练的7种常考题型归类-期末真题分类汇编(北师大版2019必修第二册)(已下线)专题7 线性代数、抽象代数与数论背景的新定义压轴大题(过关集训)
名校
解题方法
6 . 已知 ,
,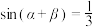 .
.
(1)证明: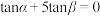 ;
;
(2)计算: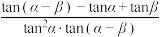 的值.
的值.
 ,
,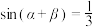 .
.(1)证明:
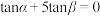 ;
;(2)计算:
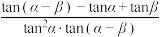 的值.
的值.
您最近一年使用:0次
2022-07-13更新
|
1264次组卷
|
4卷引用:河南省驻马店市2021-2022学年高一下学期期末数学试题
河南省驻马店市2021-2022学年高一下学期期末数学试题两角和与差的正弦、余弦和正切公式江西省宁冈中学2023届高三上学期12月月考数学(理)试题(已下线)同角三角函数基本关系式及诱导公式-一轮复习考点专练



