1 . 如图,以正方形 的边
的边 所在直线为旋转轴,其余三边旋转120°形成的面围成一个几何体
所在直线为旋转轴,其余三边旋转120°形成的面围成一个几何体 .设
.设 是
是 上的一点,
上的一点, ,
, 分别为线段
分别为线段 ,
, 的中点.
的中点. 平面
平面 ;
;
(2)若 ,求平面
,求平面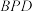 与平面
与平面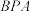 夹角的余弦值.
夹角的余弦值.
 的边
的边 所在直线为旋转轴,其余三边旋转120°形成的面围成一个几何体
所在直线为旋转轴,其余三边旋转120°形成的面围成一个几何体 .设
.设 是
是 上的一点,
上的一点, ,
, 分别为线段
分别为线段 ,
, 的中点.
的中点.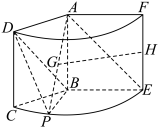
 平面
平面 ;
;(2)若
 ,求平面
,求平面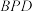 与平面
与平面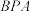 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2 . 已知过点 的直线
的直线 与圆
与圆 :
: 相交于
相交于 ,
, 两点,
两点, 的中点为
的中点为 ,过
,过 的中点
的中点 且平行于
且平行于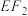 的直线交
的直线交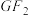 于点
于点 ,记点
,记点 的轨迹为
的轨迹为 .
.
(1)求轨迹
 的方程.
的方程.(2)若
 为轨迹
为轨迹 上的两个动点且均不在
上的两个动点且均不在 轴上,点
轴上,点 满足
满足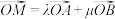 (
( ,
,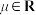 ),其中
),其中 为坐标原点,从下面①②③中选取两个作为条件,证明另外一个成立.
为坐标原点,从下面①②③中选取两个作为条件,证明另外一个成立.①点 在轨迹
在轨迹 上;②直线
上;②直线 与
与 的斜率之积为
的斜率之积为 ;③
;③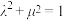 .
.
注:若选择不同的组合分别解答,则按第一个解答计分.
您最近一年使用:0次
3 . 已知双曲线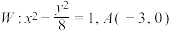 ,动直线
,动直线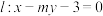 与
与 轴交于点
轴交于点 ,且与
,且与 交于
交于 两点,
两点,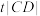 是
是 的等比中项,
的等比中项, .
.
(1)若 两点位于
两点位于 轴的同侧,求
轴的同侧,求 取最小值时
取最小值时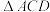 的周长;
的周长;
(2)若 ,且
,且 两点位于
两点位于 轴的异侧,证明:
轴的异侧,证明: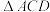 为等腰三角形.
为等腰三角形.
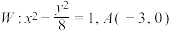 ,动直线
,动直线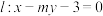 与
与 轴交于点
轴交于点 ,且与
,且与 交于
交于 两点,
两点,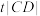 是
是 的等比中项,
的等比中项, .
.(1)若
 两点位于
两点位于 轴的同侧,求
轴的同侧,求 取最小值时
取最小值时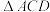 的周长;
的周长;(2)若
 ,且
,且 两点位于
两点位于 轴的异侧,证明:
轴的异侧,证明: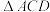 为等腰三角形.
为等腰三角形.
您最近一年使用:0次
名校
解题方法
4 . 已知 ,我们称双曲线
,我们称双曲线 与椭圆
与椭圆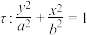 互为“伴随曲线”,点
互为“伴随曲线”,点 为双曲线
为双曲线 和椭圆
和椭圆 的下顶点.
的下顶点.
(1)若 为椭圆
为椭圆 的上顶点,直线
的上顶点,直线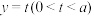 与
与 交于
交于 ,
, 两点,证明:直线
两点,证明:直线 ,
, 的交点在双曲线
的交点在双曲线 上;
上;
(2)过椭圆 的一个焦点且与长轴垂直的弦长为
的一个焦点且与长轴垂直的弦长为 ,双曲线
,双曲线 的一条渐近线方程为
的一条渐近线方程为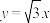 ,若
,若 为双曲线
为双曲线 的上焦点,直线
的上焦点,直线 经过
经过 且与双曲线
且与双曲线 上支交于
上支交于 ,
, 两点,记
两点,记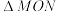 的面积为
的面积为 ,
,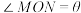 (
( 为坐标原点),
为坐标原点),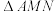 的面积为
的面积为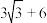 .
.
(i)求双曲线 的方程;
的方程;
(ii)证明: .
.
 ,我们称双曲线
,我们称双曲线 与椭圆
与椭圆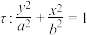 互为“伴随曲线”,点
互为“伴随曲线”,点 为双曲线
为双曲线 和椭圆
和椭圆 的下顶点.
的下顶点.(1)若
 为椭圆
为椭圆 的上顶点,直线
的上顶点,直线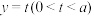 与
与 交于
交于 ,
, 两点,证明:直线
两点,证明:直线 ,
, 的交点在双曲线
的交点在双曲线 上;
上;(2)过椭圆
 的一个焦点且与长轴垂直的弦长为
的一个焦点且与长轴垂直的弦长为 ,双曲线
,双曲线 的一条渐近线方程为
的一条渐近线方程为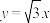 ,若
,若 为双曲线
为双曲线 的上焦点,直线
的上焦点,直线 经过
经过 且与双曲线
且与双曲线 上支交于
上支交于 ,
, 两点,记
两点,记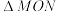 的面积为
的面积为 ,
,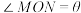 (
( 为坐标原点),
为坐标原点),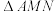 的面积为
的面积为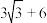 .
.(i)求双曲线
 的方程;
的方程;(ii)证明:
 .
.
您最近一年使用:0次
2024-02-08更新
|
987次组卷
|
3卷引用:福建省漳州市2024届高三毕业班第二次质量检测数学试题
名校
解题方法
5 . 已知椭圆 的中心为坐标原点
的中心为坐标原点 ,对称轴为
,对称轴为 轴、
轴、 轴,且点
轴,且点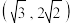 和点
和点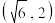 在椭圆
在椭圆 上,椭圆的左顶点与抛物线
上,椭圆的左顶点与抛物线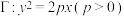 的焦点
的焦点 的距离为
的距离为 .
.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)直线 与抛物线
与抛物线 交于
交于 两点,与椭圆
两点,与椭圆 交于
交于 两点.
两点.
(ⅰ)若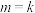 ,抛物线
,抛物线 在点
在点 处的切线交于点
处的切线交于点 ,求证:
,求证: ;
;
(ⅱ)若 ,是否存在定点
,是否存在定点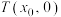 ,使得直线
,使得直线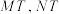 的倾斜角互补?若存在,求出
的倾斜角互补?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的中心为坐标原点
的中心为坐标原点 ,对称轴为
,对称轴为 轴、
轴、 轴,且点
轴,且点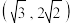 和点
和点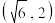 在椭圆
在椭圆 上,椭圆的左顶点与抛物线
上,椭圆的左顶点与抛物线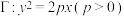 的焦点
的焦点 的距离为
的距离为 .
.(1)求椭圆
 和抛物线
和抛物线 的方程;
的方程;(2)直线
 与抛物线
与抛物线 交于
交于 两点,与椭圆
两点,与椭圆 交于
交于 两点.
两点.(ⅰ)若
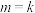 ,抛物线
,抛物线 在点
在点 处的切线交于点
处的切线交于点 ,求证:
,求证: ;
;(ⅱ)若
 ,是否存在定点
,是否存在定点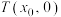 ,使得直线
,使得直线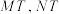 的倾斜角互补?若存在,求出
的倾斜角互补?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2023-03-14更新
|
1684次组卷
|
4卷引用:福建省漳州市2023届高三毕业班第三次质量检测数学试题
6 . 已知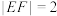 ,动点
,动点 满足:
满足: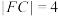 且
且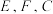 三点共面.线段
三点共面.线段 的垂直平分线为
的垂直平分线为 ,点
,点 在
在 上且
上且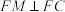 ,
, 为线段
为线段 延长线上的点,且
延长线上的点,且 ,记
,记 的轨迹为曲线
的轨迹为曲线 .
.
(1)求证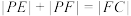 ,并建立适当的坐标系,求
,并建立适当的坐标系,求 的方程;
的方程;
(2)判断直线 与
与 公共点的个数,并说明理由.
公共点的个数,并说明理由.
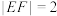 ,动点
,动点 满足:
满足: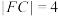 且
且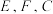 三点共面.线段
三点共面.线段 的垂直平分线为
的垂直平分线为 ,点
,点 在
在 上且
上且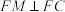 ,
, 为线段
为线段 延长线上的点,且
延长线上的点,且 ,记
,记 的轨迹为曲线
的轨迹为曲线 .
.(1)求证
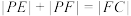 ,并建立适当的坐标系,求
,并建立适当的坐标系,求 的方程;
的方程;(2)判断直线
 与
与 公共点的个数,并说明理由.
公共点的个数,并说明理由.
您最近一年使用:0次
7 . 在平面直角坐标系 中, 设点
中, 设点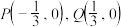 , 点
, 点 与
与 两点的距离之和为
两点的距离之和为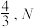 为一动点, 点
为一动点, 点 满足向量关系式:
满足向量关系式: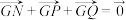 .
.
(1)求点 的轨迹方程
的轨迹方程 ;
;
(2)设 与
与 轴交于点
轴交于点 (
( 在
在 的左侧), 点
的左侧), 点 为
为 上一动点 (且不与
上一动点 (且不与 重合). 设直线
重合). 设直线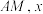 轴与直线
轴与直线 分别交于点
分别交于点 ,取
,取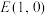 ,连接
,连接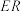 ,证明:
,证明: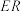 为
为 的角平分线.
的角平分线.
 中, 设点
中, 设点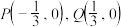 , 点
, 点 与
与 两点的距离之和为
两点的距离之和为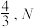 为一动点, 点
为一动点, 点 满足向量关系式:
满足向量关系式: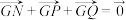 .
.(1)求点
 的轨迹方程
的轨迹方程 ;
;(2)设
 与
与 轴交于点
轴交于点 (
( 在
在 的左侧), 点
的左侧), 点 为
为 上一动点 (且不与
上一动点 (且不与 重合). 设直线
重合). 设直线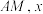 轴与直线
轴与直线 分别交于点
分别交于点 ,取
,取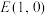 ,连接
,连接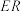 ,证明:
,证明: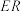 为
为 的角平分线.
的角平分线.
您最近一年使用:0次
2022-09-23更新
|
1048次组卷
|
2卷引用:福建师范大学附属中学2023届高三上学期数学月考试题(三)
名校
解题方法
8 . 已知椭圆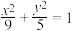 的右顶点为A,左焦点为F,过点F作斜率不为零的直线l交椭圆于
的右顶点为A,左焦点为F,过点F作斜率不为零的直线l交椭圆于 两点,连接
两点,连接 ,
, 分别交直线
分别交直线 于
于 两点,过点F且垂直于
两点,过点F且垂直于 的直线交直线
的直线交直线 于点R.
于点R.
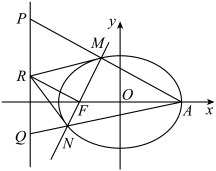
(1)求证:点R为线段 的中点;
的中点;
(2)记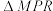 ,
,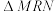 ,
,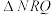 的面积分别为
的面积分别为 ,
, ,
, ,试探究:是否存在实数
,试探究:是否存在实数 使得
使得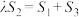 ?若存在,请求出实数
?若存在,请求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
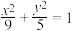 的右顶点为A,左焦点为F,过点F作斜率不为零的直线l交椭圆于
的右顶点为A,左焦点为F,过点F作斜率不为零的直线l交椭圆于 两点,连接
两点,连接 ,
, 分别交直线
分别交直线 于
于 两点,过点F且垂直于
两点,过点F且垂直于 的直线交直线
的直线交直线 于点R.
于点R.
(1)求证:点R为线段
 的中点;
的中点;(2)记
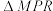 ,
,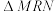 ,
,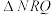 的面积分别为
的面积分别为 ,
, ,
, ,试探究:是否存在实数
,试探究:是否存在实数 使得
使得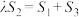 ?若存在,请求出实数
?若存在,请求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2023-03-09更新
|
2252次组卷
|
5卷引用:福建省厦门双十中学2023届高三高考适应性考试数学试题
解题方法
9 . 已知圆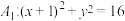 ,直线
,直线 过点
过点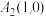 且与圆
且与圆 交于点B,C,BC中点为D,过
交于点B,C,BC中点为D,过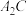 中点E且平行于
中点E且平行于 的直线交
的直线交 于点P,记P的轨迹为Γ
于点P,记P的轨迹为Γ
(1)求Γ的方程;
(2)坐标原点O关于 ,
, 的对称点分别为
的对称点分别为 ,
, ,点
,点 ,
, 关于直线
关于直线 的对称点分别为
的对称点分别为 ,
, ,过
,过 的直线
的直线 与Γ交于点M,N,直线
与Γ交于点M,N,直线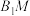 ,
, 相交于点Q.请从下列结论中,选择一个正确的结论并给予证明.
相交于点Q.请从下列结论中,选择一个正确的结论并给予证明.
①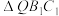 的面积是定值;②
的面积是定值;②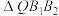 的面积是定值:③
的面积是定值:③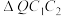 的面积是定值.
的面积是定值.
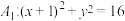 ,直线
,直线 过点
过点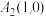 且与圆
且与圆 交于点B,C,BC中点为D,过
交于点B,C,BC中点为D,过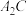 中点E且平行于
中点E且平行于 的直线交
的直线交 于点P,记P的轨迹为Γ
于点P,记P的轨迹为Γ(1)求Γ的方程;
(2)坐标原点O关于
 ,
, 的对称点分别为
的对称点分别为 ,
, ,点
,点 ,
, 关于直线
关于直线 的对称点分别为
的对称点分别为 ,
, ,过
,过 的直线
的直线 与Γ交于点M,N,直线
与Γ交于点M,N,直线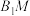 ,
, 相交于点Q.请从下列结论中,选择一个正确的结论并给予证明.
相交于点Q.请从下列结论中,选择一个正确的结论并给予证明.①
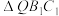 的面积是定值;②
的面积是定值;②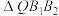 的面积是定值:③
的面积是定值:③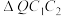 的面积是定值.
的面积是定值.
您最近一年使用:0次
名校
解题方法
10 . 已知双曲线: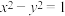 ,点M为双曲线C右支上一点,A、B为双曲线C的左、右顶点,直线
,点M为双曲线C右支上一点,A、B为双曲线C的左、右顶点,直线 与y轴交于点D,点Q在x轴正半轴上,点E在y轴上.
与y轴交于点D,点Q在x轴正半轴上,点E在y轴上.
(1)若点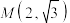 ,
, ,过点Q作BM的垂线l交该双曲线C于S,T两点,求
,过点Q作BM的垂线l交该双曲线C于S,T两点,求 的面积;
的面积;
(2)若点M不与B重合,从下面①②③中选取两个作为条件,证明另外一个成立.① ;②
;②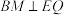 ;③
;③ .注:若选择不同的组合分别解答,则按第一个解答计分.
.注:若选择不同的组合分别解答,则按第一个解答计分.
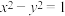 ,点M为双曲线C右支上一点,A、B为双曲线C的左、右顶点,直线
,点M为双曲线C右支上一点,A、B为双曲线C的左、右顶点,直线 与y轴交于点D,点Q在x轴正半轴上,点E在y轴上.
与y轴交于点D,点Q在x轴正半轴上,点E在y轴上.(1)若点
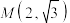 ,
, ,过点Q作BM的垂线l交该双曲线C于S,T两点,求
,过点Q作BM的垂线l交该双曲线C于S,T两点,求 的面积;
的面积;(2)若点M不与B重合,从下面①②③中选取两个作为条件,证明另外一个成立.①
 ;②
;②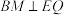 ;③
;③ .注:若选择不同的组合分别解答,则按第一个解答计分.
.注:若选择不同的组合分别解答,则按第一个解答计分.
您最近一年使用:0次
2023-04-20更新
|
2660次组卷
|
6卷引用:福建省厦门第一中学2023届高三下学期4月期中考试数学试题
福建省厦门第一中学2023届高三下学期4月期中考试数学试题广东省深圳市2023届高三二模数学试题(已下线)模块四 专题7 解析几何(已下线)专题06 解析几何(已下线)押新高考第21题 圆锥曲线(已下线)技巧04 结构不良问题解题策略(5大核心考点)(讲义)



