名校
1 . 从函数角度看,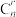 可以看成以r为自变量的函数
可以看成以r为自变量的函数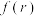 ,其定义域是
,其定义域是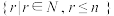 .
.
(1)画出函数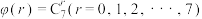 的图象;
的图象;
(2)求证: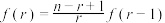 ;
;
(3)试利用(2)的结论来证明:当n为偶数时, 的展开式最中间一项的二项式系数最大;当n为奇数时,
的展开式最中间一项的二项式系数最大;当n为奇数时, 的展开式最中间两项的二项式系数相等且最大.
的展开式最中间两项的二项式系数相等且最大.
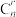 可以看成以r为自变量的函数
可以看成以r为自变量的函数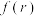 ,其定义域是
,其定义域是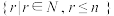 .
.(1)画出函数
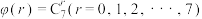 的图象;
的图象;(2)求证:
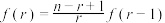 ;
;(3)试利用(2)的结论来证明:当n为偶数时,
 的展开式最中间一项的二项式系数最大;当n为奇数时,
的展开式最中间一项的二项式系数最大;当n为奇数时, 的展开式最中间两项的二项式系数相等且最大.
的展开式最中间两项的二项式系数相等且最大.
您最近半年使用:0次
2021-12-06更新
|
476次组卷
|
4卷引用:辽宁省沈阳市东北育才2021-2022学年高二下学期期初自我检测数学试题
2 . 甲进行摸球跳格游戏.图上标有第1格,第2格, ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.
(1)甲在一次摸球中摸出红球的个数记为 ,求
,求 的分布列和期望;
的分布列和期望;
(2)证明:数列 为等比数列,并求
为等比数列,并求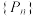 的通项公式.
的通项公式.
 ,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第
,第25格,棋子开始在第1格.盒中有5个大小相同的小球,其中3个红球,2个白球(5个球除颜色外其他都相同).每次甲在盒中随机摸出两球,记下颜色后放回盒中,若两球颜色相同,棋子向前跳1格;若两球颜色不同,棋子向前跳2格,直到棋子跳到第24格或第25格时,游戏结束.记棋子跳到第 格的概率为
格的概率为 .
.(1)甲在一次摸球中摸出红球的个数记为
 ,求
,求 的分布列和期望;
的分布列和期望;(2)证明:数列
 为等比数列,并求
为等比数列,并求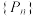 的通项公式.
的通项公式.
您最近半年使用:0次
名校
3 . 某工厂生产某种元件,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品,现抽取这种元件100件进行检测,检测结果统计如下表:
(1)现从这100件样品中随机抽取2件,若其中一件为合格品,求另一件也为合格品的概率;
(2)关于随机变量,俄国数学家切比雪夫提出切比雪夫不等式:
若随机变量X具有数学期望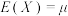 ,方差
,方差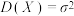 ,则对任意正数
,则对任意正数 ,均有
,均有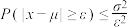 成立.
成立.
(i)若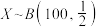 ,证明:
,证明: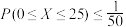 ;
;
(ii)利用该结论表示即使分布未知,随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为90%,那么根据所给样本数据,请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信?(注:当随机事件A发生的概率小于0.05时,可称事件A为小概率事件)
| 测试指标 | 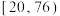 | 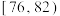 | 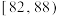 | 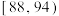 |  |
| 元件数(件) | 12 | 18 | 36 | 30 | 4 |
(2)关于随机变量,俄国数学家切比雪夫提出切比雪夫不等式:
若随机变量X具有数学期望
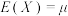 ,方差
,方差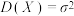 ,则对任意正数
,则对任意正数 ,均有
,均有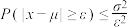 成立.
成立.(i)若
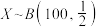 ,证明:
,证明: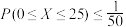 ;
;(ii)利用该结论表示即使分布未知,随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为90%,那么根据所给样本数据,请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信?(注:当随机事件A发生的概率小于0.05时,可称事件A为小概率事件)
您最近半年使用:0次
2024-04-15更新
|
2087次组卷
|
3卷引用:辽宁省2024届高三下学期3+2+1模式新高考适应性统一考试数学试卷
解题方法
4 . 设数列 的前
的前 项和为
项和为 ,已知
,已知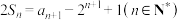 ,且
,且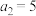 .
.
(1)证明: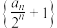 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(2)设 ,若对于任意的
,若对于任意的 ,不等式
,不等式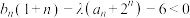 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)高斯是德国著名数学家,近代数学的奠基者之一,享有“数学王子”的称号,用他名字定义的函数称为高斯函数 ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
,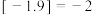 ,设
,设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求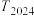 除以16的余数.
除以16的余数.
 的前
的前 项和为
项和为 ,已知
,已知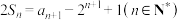 ,且
,且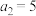 .
.(1)证明:
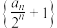 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;(2)设
 ,若对于任意的
,若对于任意的 ,不等式
,不等式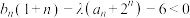 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)高斯是德国著名数学家,近代数学的奠基者之一,享有“数学王子”的称号,用他名字定义的函数称为高斯函数
 ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
,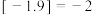 ,设
,设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求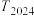 除以16的余数.
除以16的余数.
您最近半年使用:0次
2024-04-08更新
|
999次组卷
|
2卷引用:辽宁省鞍山市第六中学2024届高三下学期第二次质量检测数学试题卷
名校
解题方法
5 . 某教育教研机构为了研究学生理科思维和文科思维的差异情况,对某班级35名同学的数学成绩和语文成绩进行了统计并整理成如下2×2列联表(单位:人):
(1)能否有95%的把握认为该班数学成绩与语文成绩有关?(计算结果精确到0.001)
(2)从该班的学生中任选一人,A表示事件“选到的学生数学成绩良好”,B表示事件“选到的学生语文成绩良好”,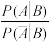 与
与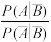 的比值是文、理科思维差异化的一项度量指标,记该指标为R.
的比值是文、理科思维差异化的一项度量指标,记该指标为R.
(i)证明: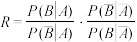 ;
;
(ii)利用该表中数据,给出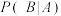 ,
,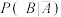 的估计值,并利用(i)的结果给出R的估计值.
的估计值,并利用(i)的结果给出R的估计值.
附: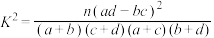 ,
,
| 数学成绩良好 | 数学成绩不够良好 | |
| 语文成绩良好 | 12 | 10 |
| 语文成绩不够良好 | 8 | 5 |
(2)从该班的学生中任选一人,A表示事件“选到的学生数学成绩良好”,B表示事件“选到的学生语文成绩良好”,
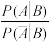 与
与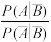 的比值是文、理科思维差异化的一项度量指标,记该指标为R.
的比值是文、理科思维差异化的一项度量指标,记该指标为R.(i)证明:
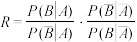 ;
;(ii)利用该表中数据,给出
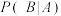 ,
,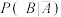 的估计值,并利用(i)的结果给出R的估计值.
的估计值,并利用(i)的结果给出R的估计值.附:
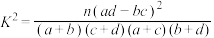 ,
,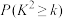 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
解题方法
6 . 在组合恒等式的证明中,构造一个具体的计数模型从而证明组合恒等式的方法叫做组合分析法,该方法体现了数学的简洁美,我们将通过如下的例子感受其妙处所在.
(1)对于 元一次方程
元一次方程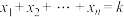 ,试求其正整数解的个数;
,试求其正整数解的个数;
(2)对于 元一次方程组
元一次方程组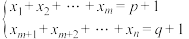 ,试求其非负整数解的个数;
,试求其非负整数解的个数;
(3)证明: (可不使用组合分析法证明).
(可不使用组合分析法证明).
注: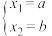 与
与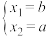 可视为二元一次方程的两组不同解.
可视为二元一次方程的两组不同解.
(1)对于
 元一次方程
元一次方程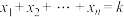 ,试求其正整数解的个数;
,试求其正整数解的个数;(2)对于
 元一次方程组
元一次方程组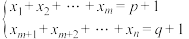 ,试求其非负整数解的个数;
,试求其非负整数解的个数;(3)证明:
 (可不使用组合分析法证明).
(可不使用组合分析法证明).注:
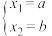 与
与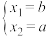 可视为二元一次方程的两组不同解.
可视为二元一次方程的两组不同解.
您最近半年使用:0次
2024-03-08更新
|
782次组卷
|
2卷引用:辽宁省2024届高三下学期3+2+1模式新高考适应性统一考试数学试卷
名校
7 . 某医科大学科研部门为研究退休人员是否患痴呆症与上网的关系,随机调查了 市100位退休人员,统计数据如下表所示:
市100位退休人员,统计数据如下表所示:
患痴呆症 | 不患痴呆症 | 合计 | |
上网 | 16 | 32 | 48 |
不上网 | 34 | 18 | 52 |
合计 | 50 | 50 | 100 |
(1)依据
 的独立性检验,能否认为该市退休人员是否患痴呆症与上网之间有关联?
的独立性检验,能否认为该市退休人员是否患痴呆症与上网之间有关联?(2)从该市退休人员中任取一位,记事件A为“此人患痴呆症”,
 为“此人上网”,则
为“此人上网”,则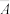 为“此人不患痴呆症”,定义事件A的强度
为“此人不患痴呆症”,定义事件A的强度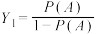 ,在事件
,在事件 发生的条件下A的强度
发生的条件下A的强度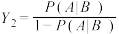 .
.(i)证明: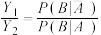 ;
;
(ⅱ)利用抽样的样本数据,估计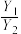 的值.
的值.
附: ,其中
,其中 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
您最近半年使用:0次
2023-11-20更新
|
718次组卷
|
5卷引用:辽宁省沈阳市第一二〇中学2023-2024学年高二上学期第四次质量监测数学试题
辽宁省沈阳市第一二〇中学2023-2024学年高二上学期第四次质量监测数学试题(已下线)2024年普通高等学校招生全国统一考试数学领航卷(七)(已下线)模块二 专题5 概率中的创新问题(已下线)4.3.2 独立性检验(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)第05讲 第八章 成对数据的统计分析 章末重点题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)
解题方法
8 . 踢毽子在我国流传很广,有着悠久的历史,是一项传统民间体育活动.某次体育课上,甲、乙、1丙、丁四人一起踢毽子.毽子在四人中传递,先从甲开始,甲传给乙、丙、丁的概率均为 ;当乙接到毽子时,乙传给甲、丙、丁的概率分别为
;当乙接到毽子时,乙传给甲、丙、丁的概率分别为 ,
, ,
, ;当丙接到毽子时,丙传给甲、乙、丁的概率分别为
;当丙接到毽子时,丙传给甲、乙、丁的概率分别为 ,
, ,
, ;当丁接到毽子时,丁传给甲、乙、丙的概率分别为
;当丁接到毽子时,丁传给甲、乙、丙的概率分别为 ,
, ,
, .假设毽子一直没有掉地上,经过
.假设毽子一直没有掉地上,经过 次传毽子后,毽子被甲、乙、丙、丁接到的概率分别为
次传毽子后,毽子被甲、乙、丙、丁接到的概率分别为 ,
, ,
,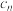 ,
,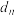 ,已知
,已知 .
.
(1)记丁在前2次传毽子中,接到毽子的次数为 ,求
,求 的分布列;
的分布列;
(2)证明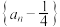 为等比数列,并判断经过150次传毽子后甲接到毽子的概率与
为等比数列,并判断经过150次传毽子后甲接到毽子的概率与 的大小.
的大小.
 ;当乙接到毽子时,乙传给甲、丙、丁的概率分别为
;当乙接到毽子时,乙传给甲、丙、丁的概率分别为 ,
, ,
, ;当丙接到毽子时,丙传给甲、乙、丁的概率分别为
;当丙接到毽子时,丙传给甲、乙、丁的概率分别为 ,
, ,
, ;当丁接到毽子时,丁传给甲、乙、丙的概率分别为
;当丁接到毽子时,丁传给甲、乙、丙的概率分别为 ,
, ,
, .假设毽子一直没有掉地上,经过
.假设毽子一直没有掉地上,经过 次传毽子后,毽子被甲、乙、丙、丁接到的概率分别为
次传毽子后,毽子被甲、乙、丙、丁接到的概率分别为 ,
, ,
,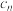 ,
,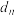 ,已知
,已知 .
.(1)记丁在前2次传毽子中,接到毽子的次数为
 ,求
,求 的分布列;
的分布列;(2)证明
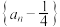 为等比数列,并判断经过150次传毽子后甲接到毽子的概率与
为等比数列,并判断经过150次传毽子后甲接到毽子的概率与 的大小.
的大小.
您最近半年使用:0次
名校
解题方法
9 . 甲、乙两名同学积极参与体育锻炼,对同一体育项目,在一段时间内甲进行了6次测试,乙进行了7次测试.每次测试满分均为100分,达到85分及以上为优秀.两位同学的测试成绩如下表:
(1)从甲、乙两名同学共进行的13次测试中随机选取一次,求该次测试成绩超过90分的概率;
(2)从甲同学进行的6次测试中随机选取4次,设X表示这4次测试成绩达到优秀的次数,求X的分布列及数学期望EX;
(3)从乙同学进行的7次测试中随机选取3次,设Y表示这3次测试成绩达到优秀的次数,试判断数学期望EY与(2)中EX的大小.(结论不要求证明)
次数 同学 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
甲 | 80 | 78 | 82 | 86 | 95 | 93 | — |
乙 | 76 | 81 | 80 | 85 | 89 | 96 | 94 |
(2)从甲同学进行的6次测试中随机选取4次,设X表示这4次测试成绩达到优秀的次数,求X的分布列及数学期望EX;
(3)从乙同学进行的7次测试中随机选取3次,设Y表示这3次测试成绩达到优秀的次数,试判断数学期望EY与(2)中EX的大小.(结论不要求证明)
您最近半年使用:0次
2023-03-27更新
|
1332次组卷
|
5卷引用:辽宁省沈阳市东北育才学校2023届高三下学期适应性考试数学试题
名校
10 . 我们将服从二项分布的随机变量称为二项随机变量,服从正态分布的随机变量称为正态随机变量.概率论中有一个重要的结论是棣莫弗—拉普拉斯极限定理,它表明,若随机变量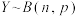 ,当
,当 充分大时,二项随机变量
充分大时,二项随机变量 可以由正态随机变量
可以由正态随机变量 来近似,且正态随机变量
来近似,且正态随机变量 的期望和方差与二项随机变量
的期望和方差与二项随机变量 的期望和方差相同.棣莫弗在1733年证明了
的期望和方差相同.棣莫弗在1733年证明了 的特殊情形.1812年,拉普拉斯对一般的
的特殊情形.1812年,拉普拉斯对一般的 进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数不超过60次的概率为
进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数不超过60次的概率为______ .
(附:若 ,则
,则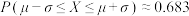 ,
,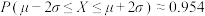 ,
,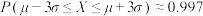 )
)
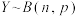 ,当
,当 充分大时,二项随机变量
充分大时,二项随机变量 可以由正态随机变量
可以由正态随机变量 来近似,且正态随机变量
来近似,且正态随机变量 的期望和方差与二项随机变量
的期望和方差与二项随机变量 的期望和方差相同.棣莫弗在1733年证明了
的期望和方差相同.棣莫弗在1733年证明了 的特殊情形.1812年,拉普拉斯对一般的
的特殊情形.1812年,拉普拉斯对一般的 进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数不超过60次的概率为
进行了证明.现抛掷一枚质地均匀的硬币100次,则利用正态分布近似估算硬币正面向上次数不超过60次的概率为(附:若
 ,则
,则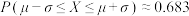 ,
,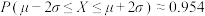 ,
,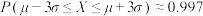 )
)
您最近半年使用:0次
2023-07-18更新
|
222次组卷
|
3卷引用:辽宁省沈阳市辽宁实验中学北校2023-2024学年高二下学期4月阶段测试数学试题





