解题方法
1 . 已知随机性离散变量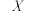 的分布列如下,则
的分布列如下,则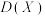 的值可以是( )
的值可以是( )
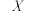 的分布列如下,则
的分布列如下,则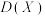 的值可以是( )
的值可以是( )
| 0 | 1 | 2 |
|
|
|
|
A.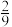 | B.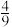 | C.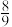 | D.1 |
您最近一年使用:0次
名校
解题方法
2 . 第十四届全国冬季运动会雪橇项目比赛于2023年12月16日至17日在北京延庆举行,赛程时间安排如下表:
(1)若小明在每天各随机观看一场比赛,求他恰好看到单人雪橇和双人雪橇的概率;
(2)若小明在这两天的所有比赛中随机观看三场,记 为看到双人雪橇的次数,求
为看到双人雪橇的次数,求 的分布列及期望
的分布列及期望 ;
;
(3)若小明在每天各随机观看一场比赛,用“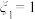 ”表示小明在周六看到单人雪橇,“
”表示小明在周六看到单人雪橇,“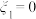 ” 表示小明在周六没看到单人雪橇,“
” 表示小明在周六没看到单人雪橇,“ ”表示小明在周日看到单人雪橇,“
”表示小明在周日看到单人雪橇,“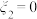 ”表示小明在周日没看到单人雪橇,写出方差
”表示小明在周日没看到单人雪橇,写出方差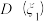 ,
,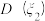 的大小关系.
的大小关系.
12月16日 | 星期六 | 9:30 | 单人雪橇第1轮 |
10:30 | 单人雪橇第2轮 | ||
15:30 | 双人雪橇第1轮 | ||
16:30 | 双人雪橇第2轮 | ||
12月17日 | 星期日 | 9:30 | 单人雪橇第3轮 |
10:30 | 单人雪橇第4轮 | ||
15:30 | 团体接力 |
(2)若小明在这两天的所有比赛中随机观看三场,记
 为看到双人雪橇的次数,求
为看到双人雪橇的次数,求 的分布列及期望
的分布列及期望 ;
;(3)若小明在每天各随机观看一场比赛,用“
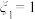 ”表示小明在周六看到单人雪橇,“
”表示小明在周六看到单人雪橇,“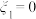 ” 表示小明在周六没看到单人雪橇,“
” 表示小明在周六没看到单人雪橇,“ ”表示小明在周日看到单人雪橇,“
”表示小明在周日看到单人雪橇,“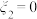 ”表示小明在周日没看到单人雪橇,写出方差
”表示小明在周日没看到单人雪橇,写出方差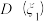 ,
,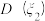 的大小关系.
的大小关系.
您最近一年使用:0次
2024-03-12更新
|
1030次组卷
|
3卷引用:2024届北京市延庆区高考一模数学试题
名校
解题方法
3 . 2022年二十国集团领导人第十七次峰会11月16日在印度尼西亚巴厘岛闭幕,峰会通过《二十国集团领导人巴厘岛峰会宣言》.宣言说,值此全球经济关键时刻,二十国集团采取切实、精准、迅速和必要的行动至关重要,基于主席国印尼提出的“共同复苏、强劲复苏”主题,各国将采取协调行动,推进强劲、包容、韧性的全球复苏以及创造就业和增长的可持续发展、中国采取负责任的态度,积极推动产业的可持续发展,并对友好国家进行技术援助。非洲某芯片企业生产芯片I有四道工序,前三道工序的生产互不影响,第四道是检测评估工序,包括智能自动检测与人工抽检.
(1)在中国企业援助前,该芯片企业生产芯片I的前三道工序的次品率分别为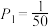 ,
, ,
,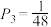 .
.
①求生产该芯片 的前三道工序的次品率
的前三道工序的次品率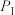 ;
;
②第四道工序中,智能自动检测为次品的芯片会被自动淘汰,合格的芯片进入流水线并由工人进行抽查检验.已知芯片I智能自动检测显示合格率为 ,求工人在流水线进行人工抽检时,抽检一个芯片,该芯片恰为合格品的概率;
,求工人在流水线进行人工抽检时,抽检一个芯片,该芯片恰为合格品的概率;
(2)该芯片企业在中国企业援助下,改进生产工艺并生产了芯片II.某手机生产厂商获得芯片I与芯片II,并在某款新型手机上使用.现对使用这款手机的用户回访,对开机速度进行满意度调查,据统计,回访的100名用户中,安装芯片I的有40部,其中对开机速度满意的占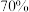 ;安装芯片II的有60部,其中对开机速度满意的占
;安装芯片II的有60部,其中对开机速度满意的占 .现采用分层抽样的方法从开机速度满意的人群中抽取6人,再从这6人中选取3人进行座谈,记抽到对安装芯片II的手机开机速度满意的人数为
.现采用分层抽样的方法从开机速度满意的人群中抽取6人,再从这6人中选取3人进行座谈,记抽到对安装芯片II的手机开机速度满意的人数为 ,求
,求 的分布列及其数学期望.
的分布列及其数学期望.
(1)在中国企业援助前,该芯片企业生产芯片I的前三道工序的次品率分别为
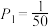 ,
, ,
,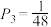 .
.①求生产该芯片
 的前三道工序的次品率
的前三道工序的次品率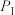 ;
;②第四道工序中,智能自动检测为次品的芯片会被自动淘汰,合格的芯片进入流水线并由工人进行抽查检验.已知芯片I智能自动检测显示合格率为
 ,求工人在流水线进行人工抽检时,抽检一个芯片,该芯片恰为合格品的概率;
,求工人在流水线进行人工抽检时,抽检一个芯片,该芯片恰为合格品的概率;(2)该芯片企业在中国企业援助下,改进生产工艺并生产了芯片II.某手机生产厂商获得芯片I与芯片II,并在某款新型手机上使用.现对使用这款手机的用户回访,对开机速度进行满意度调查,据统计,回访的100名用户中,安装芯片I的有40部,其中对开机速度满意的占
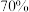 ;安装芯片II的有60部,其中对开机速度满意的占
;安装芯片II的有60部,其中对开机速度满意的占 .现采用分层抽样的方法从开机速度满意的人群中抽取6人,再从这6人中选取3人进行座谈,记抽到对安装芯片II的手机开机速度满意的人数为
.现采用分层抽样的方法从开机速度满意的人群中抽取6人,再从这6人中选取3人进行座谈,记抽到对安装芯片II的手机开机速度满意的人数为 ,求
,求 的分布列及其数学期望.
的分布列及其数学期望.
您最近一年使用:0次
名校
4 . 某校举行知识竞赛,最后一个名额要在A,B两名同学中产生,测试方案如下:A,B两名学生各自从给定的4个问题中随机抽取3个问题作答,在这4个问题中,已知A能正确作答其中的3个,B能正确作答每个问题的概率都是 ,A,B两名同学作答问题相互独立.
,A,B两名同学作答问题相互独立.
(1)求A,B两名同学恰好共答对2个问题的概率;
(2)若让你投票决定参赛选手,你会选择哪名学生,简要说明理由.
 ,A,B两名同学作答问题相互独立.
,A,B两名同学作答问题相互独立.(1)求A,B两名同学恰好共答对2个问题的概率;
(2)若让你投票决定参赛选手,你会选择哪名学生,简要说明理由.
您最近一年使用:0次
名校
5 . 已知随机变量 的分布列如下:
的分布列如下:
则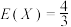 是
是 的( )
的( )
 的分布列如下:
的分布列如下:
| 1 | 2 |
|
|
|
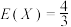 是
是 的( )
的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近一年使用:0次
2024-03-07更新
|
2415次组卷
|
11卷引用:广东省2024届高三百日冲刺联合学业质量监测(一模)数学试题
广东省2024届高三百日冲刺联合学业质量监测(一模)数学试题山东省菏泽市第一中学人民路校区2024届高三下学期2月月考数学试题(已下线)1.2 常用逻辑用语(十年高考)(已下线)第三套 艺体生新高考全真模拟 (一模重组卷)(已下线)1.2 常用逻辑用语(高考真题素材之十年高考)(已下线)7.3离散型随机变量的数字特征 第二课 归纳核心考点江西省丰城中学2023-2024学年高二下学期3月月考数学试题(已下线)第七章 随机变量及其分布总结 第一练 考点强化训练(已下线)7.3.2 离散型随机变量的方差——课后作业(巩固版)单元测试B卷——第七章 随机变量及其分布(已下线)7.3 离散型随机变量的数字特征(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)
6 . 某商场推出购物抽奖促销活动,活动规则如下:
①顾客在商场内消费每满100元,可获得1张抽奖券;
②顾客进行一次抽奖需消耗1张抽奖券,抽奖规则为:从放有5个白球,1个红球的盒子中,随机摸取1个球(每个球被摸到的可能性相同),若摸到白球,则没有中奖,若摸到红球,则可获得1份礼品,并得到一次额外抽奖机会(额外抽奖机会不消耗抽奖券,抽奖规则不变);
③每位顾客获得的礼品数不超过3份,若获得的礼品数满3份,则不可继续抽奖;
(1)顾客甲通过在商场内消费获得了2张抽奖券,求他通过抽奖至少获得1份礼品的概率;
(2)顾客乙累计消耗3张抽奖券抽奖后,获得的礼品数满3份,则他在消耗第2张抽奖券抽奖的过程中,获得礼品的概率是多少?
(3)设顾客在消耗 张抽奖券抽奖后,获得的礼品数满3份,要获得
张抽奖券抽奖后,获得的礼品数满3份,要获得 张抽奖券,至少要在商场中消费满
张抽奖券,至少要在商场中消费满 元,求
元,求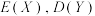 的值.
的值.
(重复进行某个伯努利试验,且每次试验的成功概率均为 .随机变量
.随机变量 表示当恰好出现
表示当恰好出现 次失败时已经成功的试验次数.则
次失败时已经成功的试验次数.则 服从参数为
服从参数为 和
和 的负二项分布.记作
的负二项分布.记作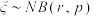 .它的均值
.它的均值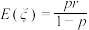 ,方差
,方差 )
)
①顾客在商场内消费每满100元,可获得1张抽奖券;
②顾客进行一次抽奖需消耗1张抽奖券,抽奖规则为:从放有5个白球,1个红球的盒子中,随机摸取1个球(每个球被摸到的可能性相同),若摸到白球,则没有中奖,若摸到红球,则可获得1份礼品,并得到一次额外抽奖机会(额外抽奖机会不消耗抽奖券,抽奖规则不变);
③每位顾客获得的礼品数不超过3份,若获得的礼品数满3份,则不可继续抽奖;
(1)顾客甲通过在商场内消费获得了2张抽奖券,求他通过抽奖至少获得1份礼品的概率;
(2)顾客乙累计消耗3张抽奖券抽奖后,获得的礼品数满3份,则他在消耗第2张抽奖券抽奖的过程中,获得礼品的概率是多少?
(3)设顾客在消耗
 张抽奖券抽奖后,获得的礼品数满3份,要获得
张抽奖券抽奖后,获得的礼品数满3份,要获得 张抽奖券,至少要在商场中消费满
张抽奖券,至少要在商场中消费满 元,求
元,求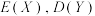 的值.
的值.(重复进行某个伯努利试验,且每次试验的成功概率均为
 .随机变量
.随机变量 表示当恰好出现
表示当恰好出现 次失败时已经成功的试验次数.则
次失败时已经成功的试验次数.则 服从参数为
服从参数为 和
和 的负二项分布.记作
的负二项分布.记作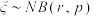 .它的均值
.它的均值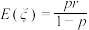 ,方差
,方差 )
)
您最近一年使用:0次
名校
7 . 在一组样本数据中,1,2,3,4出现的频率分别为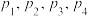 ,且
,且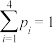 ,则下面四种情形中,对应样本的标准差最小的一组是( )
,则下面四种情形中,对应样本的标准差最小的一组是( )
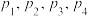 ,且
,且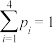 ,则下面四种情形中,对应样本的标准差最小的一组是( )
,则下面四种情形中,对应样本的标准差最小的一组是( )A. | B.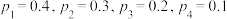 |
C. | D.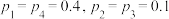 |
您最近一年使用:0次
2024-03-03更新
|
599次组卷
|
6卷引用:安徽省蚌埠市2024届高三下学期第三次教学质量检查数学试题
安徽省蚌埠市2024届高三下学期第三次教学质量检查数学试题(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)河南省信阳市新县高级中学2024届高三考前第六次适应性考试数学试题
名校
8 . 设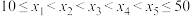 ,随机变量
,随机变量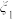 取值
取值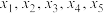 的概率均为0.2,随机变量
的概率均为0.2,随机变量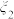 取值
取值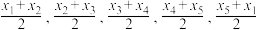 的概率也均为0.2,若记
的概率也均为0.2,若记 分别为
分别为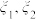 的方差,则( )
的方差,则( )
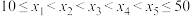 ,随机变量
,随机变量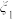 取值
取值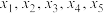 的概率均为0.2,随机变量
的概率均为0.2,随机变量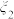 取值
取值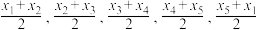 的概率也均为0.2,若记
的概率也均为0.2,若记 分别为
分别为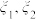 的方差,则( )
的方差,则( )A.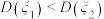 |
B. |
C.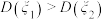 |
D.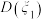 与 与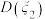 的大小关系与 的大小关系与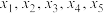 的取值有关 的取值有关 |
您最近一年使用:0次
2024-03-03更新
|
1267次组卷
|
5卷引用:广东省广州市天河区2024届高三毕业班综合测试(二)数学试卷
广东省广州市天河区2024届高三毕业班综合测试(二)数学试卷山东省菏泽市第一中学八一路校区2024届高三下学期2月月考数学试题(已下线)高二下学期期中复习选择题压轴题十五大题型专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)压轴题03不等式压轴题13题型汇总 -1湖北省武汉市第十一中学2023-2024学年高二下学期6月考数学试题
名校
解题方法
9 . 设离散型随机变量 的分布列为:
的分布列为:
若离散型随机变量 满足
满足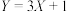 ,则( )
,则( )
 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
| 0.4 | 0.3 | 0.2 |
 满足
满足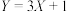 ,则( )
,则( )A. | B. |
C. | D. |
您最近一年使用:0次
2024-02-23更新
|
1297次组卷
|
4卷引用:江西省部分学校2023-2024学年高二上学期1月期末数学试题
江西省部分学校2023-2024学年高二上学期1月期末数学试题(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)江西八所重点中学2024届高三联考考后提升数学模拟训练一
名校
10 . 某校高二(1)班的元旦联欢会设计了一项抽奖游戏:准备了 张相同的卡片,其中只在
张相同的卡片,其中只在 张卡片上印有“奖”字.
张卡片上印有“奖”字.
(1)采取放回抽样方式,从中依次抽取 张卡片,求抽到印有“奖”字卡片张数
张卡片,求抽到印有“奖”字卡片张数 的分布列、数学期望及方差;
的分布列、数学期望及方差;
(2)采取不放回抽样方式,从中依次抽取 张卡片,求第一次抽到印有“奖”字卡片的条件下,第三次抽到未印有“奖”字卡片的概率.
张卡片,求第一次抽到印有“奖”字卡片的条件下,第三次抽到未印有“奖”字卡片的概率.
 张相同的卡片,其中只在
张相同的卡片,其中只在 张卡片上印有“奖”字.
张卡片上印有“奖”字.(1)采取放回抽样方式,从中依次抽取
 张卡片,求抽到印有“奖”字卡片张数
张卡片,求抽到印有“奖”字卡片张数 的分布列、数学期望及方差;
的分布列、数学期望及方差;(2)采取不放回抽样方式,从中依次抽取
 张卡片,求第一次抽到印有“奖”字卡片的条件下,第三次抽到未印有“奖”字卡片的概率.
张卡片,求第一次抽到印有“奖”字卡片的条件下,第三次抽到未印有“奖”字卡片的概率.
您最近一年使用:0次
2024-01-25更新
|
706次组卷
|
2卷引用:广西桂林市2023-2024学年高二上学期数学期末质量检测数学试题








