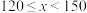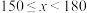2024高三·全国·专题练习
名校
1 . 某短视频软件经过几年的快速发展,深受人们的喜爱,该软件除了有娱乐属性外,也可通过平台推送广告.某公司为了宣传新产品,现有以下两种宣传方案:
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且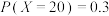 ,期望
,期望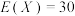 .
.
方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为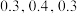 .
.
(1)请写出方案一的分布列,并求方差 ;
;
(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
方案一:投放该平台广告,据市场调研,其收益X分别为0元,20万元,40万元,且
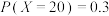 ,期望
,期望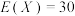 .
.方案二:投放传统广告,据市场调研,其收益Y分别为10万元,20万元,30万元,其概率依次为
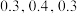 .
.(1)请写出方案一的分布列,并求方差
 ;
;(2)请你根据所学的统计知识给出建议,该公司宣传应该投放哪种广告?并说明你的理由.
您最近一年使用:0次
2024-01-07更新
|
727次组卷
|
7卷引用:专题02 结论探索型【练】【北京版】
(已下线)专题02 结论探索型【练】【北京版】(已下线)7.3.2离散型随机变量的方差(分层练习,8大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)专题7.7 随机变量及其分布全章十一大基础题型归纳(基础篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)第09讲 第七章随机变量及其分布章末题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)广东省东莞市七校2023-2024学年高二下学期5月联考数学试题陕西省咸阳市武功县普集高级中学2023-2024学年高二下学期6月月考数学试题(已下线)专题03 第七章 随机变量及其分布列--高二期末考点大串讲(人教A版2019)
2 . 某人欲投资10万元,有两种方案可供选择.设X表示方案一所得收益(单位:万元),Y表示方案二所得收益(单位:万元).其分布列分别为:
假定同期银行利率为1.75%,该人征求你的意见,你通过分析会得到怎样的结论呢?
| X | −2 | 8 |
| P | 0.7 | 0.3 |
| Y | −3 | 12 |
| P | 0.7 | 0.3 |
您最近一年使用:0次
2023-10-05更新
|
92次组卷
|
2卷引用:湘教版(2019)选择性必修第二册课本例题3.2.4离散型随机变量的方差
3 . 某高校设计了一个实验学科的考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作,规定至少正确完成其中
题,按照题目要求独立完成全部实验操作,规定至少正确完成其中 题才可提交通过.已知
题才可提交通过.已知 道备选题中考生甲有
道备选题中考生甲有 道题能正确完成,
道题能正确完成, 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲考生正确完成实验操作的题数的分布列,并计算均值;
(2)试从甲、乙两位考生正确完成实验操作的题数的均值、方差及至少正确完成 题的概率方面比较两位考生的实验操作能力.
题的概率方面比较两位考生的实验操作能力.
 道备选题中一次性随机抽取
道备选题中一次性随机抽取 题,按照题目要求独立完成全部实验操作,规定至少正确完成其中
题,按照题目要求独立完成全部实验操作,规定至少正确完成其中 题才可提交通过.已知
题才可提交通过.已知 道备选题中考生甲有
道备选题中考生甲有 道题能正确完成,
道题能正确完成, 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)求甲考生正确完成实验操作的题数的分布列,并计算均值;
(2)试从甲、乙两位考生正确完成实验操作的题数的均值、方差及至少正确完成
 题的概率方面比较两位考生的实验操作能力.
题的概率方面比较两位考生的实验操作能力.
您最近一年使用:0次
2023-10-31更新
|
836次组卷
|
3卷引用:湖南省邵阳市邵东创新实验学校2023-2024学年高三上学期第三次月考数学试题
湖南省邵阳市邵东创新实验学校2023-2024学年高三上学期第三次月考数学试题(已下线)6.4.1二项分布(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)湖南省常德市第一中学2023-2024学年高二下学期第一次月考数学试题
4 . 某企业拟定4种改革方案,经统计它们在该企业的支持率分别为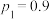 ,
,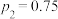 ,
, ,
, ,用“
,用“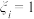 ”表示员工支持第
”表示员工支持第 种方案,用“
种方案,用“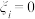 ”表示员工不支持第
”表示员工不支持第 种方案
种方案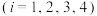 ,那么方差
,那么方差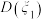 ,
,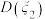 ,
, ,
,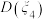 的大小关系为( )
的大小关系为( )
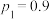 ,
,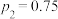 ,
, ,
, ,用“
,用“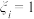 ”表示员工支持第
”表示员工支持第 种方案,用“
种方案,用“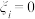 ”表示员工不支持第
”表示员工不支持第 种方案
种方案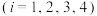 ,那么方差
,那么方差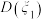 ,
,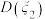 ,
, ,
,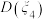 的大小关系为( )
的大小关系为( )A.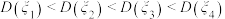 |
B.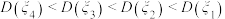 |
C.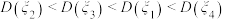 |
D.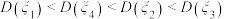 |
您最近一年使用:0次
2023-07-10更新
|
414次组卷
|
4卷引用:北京市第十二中学2022-2023学年高二下学期期末考试数学试题
北京市第十二中学2022-2023学年高二下学期期末考试数学试题(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)【北京专用】专题06概率与统计(第一部分)-高二上学期名校期末好题汇编(已下线)必考考点6 离散型随机变量与分布列 专题讲解 (期末考试必考的10大核心考点)
名校
5 . 甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从 道备选题中一次性随机抽取
道备选题中一次性随机抽取 道题,按照答对题目的个数为标准进行筛选.已知
道题,按照答对题目的个数为标准进行筛选.已知 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成, 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列;
(2)请从均值和方差的角度分析比较甲、乙两人谁的面试通过的可能性较大?
 道备选题中一次性随机抽取
道备选题中一次性随机抽取 道题,按照答对题目的个数为标准进行筛选.已知
道题,按照答对题目的个数为标准进行筛选.已知 道备选题中应聘者甲有
道备选题中应聘者甲有 道题能正确完成,
道题能正确完成, 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列;
(2)请从均值和方差的角度分析比较甲、乙两人谁的面试通过的可能性较大?
您最近一年使用:0次
2023-06-24更新
|
939次组卷
|
7卷引用:山东省临沂市2022-2023学年高二下学期期中数学试题
山东省临沂市2022-2023学年高二下学期期中数学试题广东省珠海市香樟中学2022-2023学年高二下学期6月月考数学试题(已下线)模块一 专题7 区分超几何分布与二项分布问题(已下线)考点巩固卷26分布列及三大分布(十一大考点)-2吉林省延边第二中学2023-2024学年高二上学期第二次阶段检测数学试卷广东省江门市新会第一中学等2023-2024学年高二下学期5月联考数学试题(已下线)专题01 高二下期末真题精选(2)--高二期末考点大串讲(人教A版2019)
名校
6 . 某校举行知识竞赛,最后一个名额要在 、
、 两名同学中产生,测试方案如下:
两名同学中产生,测试方案如下: 、
、 两名学生各自从给定的
两名学生各自从给定的 个问题中随机抽取
个问题中随机抽取 个问题作答,在这
个问题作答,在这 个问题中,已知
个问题中,已知 能正确作答其中的
能正确作答其中的 个,
个, 能正确作答每个问题的概率是
能正确作答每个问题的概率是 ,
, 、
、 两名同学作答问题相互独立.
两名同学作答问题相互独立.
(1)设 答对的题数为
答对的题数为 ,求
,求 的分布列;
的分布列;
(2)设 答对的题数为
答对的题数为 ,若让你投票决定参赛选手,你会选择哪名学生,并说明理由.
,若让你投票决定参赛选手,你会选择哪名学生,并说明理由.
 、
、 两名同学中产生,测试方案如下:
两名同学中产生,测试方案如下: 、
、 两名学生各自从给定的
两名学生各自从给定的 个问题中随机抽取
个问题中随机抽取 个问题作答,在这
个问题作答,在这 个问题中,已知
个问题中,已知 能正确作答其中的
能正确作答其中的 个,
个, 能正确作答每个问题的概率是
能正确作答每个问题的概率是 ,
, 、
、 两名同学作答问题相互独立.
两名同学作答问题相互独立.(1)设
 答对的题数为
答对的题数为 ,求
,求 的分布列;
的分布列;(2)设
 答对的题数为
答对的题数为 ,若让你投票决定参赛选手,你会选择哪名学生,并说明理由.
,若让你投票决定参赛选手,你会选择哪名学生,并说明理由.
您最近一年使用:0次
2023-04-10更新
|
809次组卷
|
5卷引用:黑龙江省哈尔滨市第九中学校2022-2023学年高二下学期4月月考数学试题
黑龙江省哈尔滨市第九中学校2022-2023学年高二下学期4月月考数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)(已下线)7.3.2离散型随机变量的方差 (分层作业)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)第7.3.2讲 离散型随机变量的方差-2023-2024学年新高二数学同步精讲精练宝典(人教A版2019选修第三册)【巩固卷】第3章 概率素养检测 单元测试A-湘教版(2019)选择性必修第二册
7 . 某商场为刺激消费,拟按以下方案进行促销:顾客消费每满500元便得到奖券1张,每张奖券的中奖概率为 ,且每张奖券是否中奖是相互独立的,若中奖,则商场返回顾客现金100元某顾客现购买单价为2300元的台式电脑一台,得到奖券4张.
,且每张奖券是否中奖是相互独立的,若中奖,则商场返回顾客现金100元某顾客现购买单价为2300元的台式电脑一台,得到奖券4张.
(1)设4张奖券中中奖的张数为 ,求
,求 的分布列;
的分布列;
(2)设该顾客购买台式电脑的实际支出为 (单位:元),用
(单位:元),用 表示
表示 ,并求
,并求 的数学期望和方差.
的数学期望和方差.
 ,且每张奖券是否中奖是相互独立的,若中奖,则商场返回顾客现金100元某顾客现购买单价为2300元的台式电脑一台,得到奖券4张.
,且每张奖券是否中奖是相互独立的,若中奖,则商场返回顾客现金100元某顾客现购买单价为2300元的台式电脑一台,得到奖券4张.(1)设4张奖券中中奖的张数为
 ,求
,求 的分布列;
的分布列;(2)设该顾客购买台式电脑的实际支出为
 (单位:元),用
(单位:元),用 表示
表示 ,并求
,并求 的数学期望和方差.
的数学期望和方差.
您最近一年使用:0次
解题方法
8 . 1933年7月11日,中华苏维埃共和国临时中央政府将8月1日作为中国工农红军成立纪念日.中华人民共和国成立后,将此纪念日改称为中国人民解放军建军节.为庆祝建军节,某校举行“强国强军”知识竞赛.该校某班经过层层筛选,还有最后一个参赛名额要在A,B两名学生中产生,该班班委设计了一个测试方案:A,B两名学生各自从6个问题中随机抽取3个问题作答,根据答题情况确定参赛学生.已知这6个问题中,学生A能正确回答其中的4个问题,而学生B能正确回答每个问题的概率均为 ,A,B两名学生对每个问题回答的正确与否都是相互独立的.设学生A答对题数为
,A,B两名学生对每个问题回答的正确与否都是相互独立的.设学生A答对题数为 ,学生B答对题数为
,学生B答对题数为 ,若让你投票选择参赛选手,你会选择哪名学生?请说明理由.
,若让你投票选择参赛选手,你会选择哪名学生?请说明理由.
 ,A,B两名学生对每个问题回答的正确与否都是相互独立的.设学生A答对题数为
,A,B两名学生对每个问题回答的正确与否都是相互独立的.设学生A答对题数为 ,学生B答对题数为
,学生B答对题数为 ,若让你投票选择参赛选手,你会选择哪名学生?请说明理由.
,若让你投票选择参赛选手,你会选择哪名学生?请说明理由.
您最近一年使用:0次
9 . 某校为了提升学生的科学素养、本学期初开始动员学生利用课外时间阅读科普读物、为了了解学生平均每周课外阅读科普读物所花的时间、学期末该校通过简单随机抽样的方法收集了20名学生平均每周课外阅读的时间(分钟)的数据、得到如表统计表(设 表示阅读时间,单位:分钟)
表示阅读时间,单位:分钟)
(1)完成下面的 列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?
列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?
附: .
.
(2)为了选出1名选手代表学校参加全市中小学生科普知识比赛,学校组织了考组对选手人选进行考核,经过层层筛选,甲、乙两名学生成为进入最后阶段的备选选手.考核组设计了最终确定人选的方案:请甲、乙两名学生从6道试题中随机抽取3道试题作答,已知这6道试题中,甲可正确回答其中的4道题目,而乙能正确回答每道题目的概率均为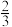 ,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
 表示阅读时间,单位:分钟)
表示阅读时间,单位:分钟)组别 | 时间分组 | 频数 | 男生人数 | 女生人数 |
1 |
| 2 | 1 | 1 |
2 |
| 10 | 4 | 6 |
3 |
| 4 | 3 | 1 |
4 |
| 2 | 1 | 1 |
5 |
| 2 | 2 | 0 |
 列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?
列联表、并回答能有90%的把认为“平均每周至少阅读120分钟与性别有关”?平均每周阅读时间不少于120分钟 | 平均每周阅读时间少于120分钟 | 合计 | |
男 | |||
女 | |||
合计 |
 .
.
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
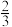 ,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
,甲、乙两名学生对每题的回答都是相互独立,互不影响的.若从数学期望和方差的角度进行分析,请问:甲、乙中哪位学生最终入选的可能性更大?
您最近一年使用:0次
2021-08-25更新
|
322次组卷
|
2卷引用:广东省韶关市2020-2021学年高二下学期期末数学试题
名校
解题方法
10 . 1933年7月11日,中华苏维埃共和国临时中央政府根据中央革命军事委员会6月30日的建议,决定8月1日为中国工农红军成立纪念日,中华人民共和国成立后,将此纪念日改称为中国人民解放军建军节,为庆祝建军节,某校举行“强国强军”知识竞赛,该校某班经过层层筛选,还有最后一个参赛名额要在 ,
, 两名学生中间产生,该班委设计了一个测试方案:
两名学生中间产生,该班委设计了一个测试方案: ,
, 两名学生各自从6个问题中随机抽取3个问题作答,已知这6个问题中,学生
两名学生各自从6个问题中随机抽取3个问题作答,已知这6个问题中,学生 能正确回答其中的4个问题,而学生
能正确回答其中的4个问题,而学生 能正确回答每个问题的概率均为
能正确回答每个问题的概率均为 ,
, ,
, 两名学生对每个问题回答正确与否都是相互独立、互不影响的.
两名学生对每个问题回答正确与否都是相互独立、互不影响的.
(1)求 恰好答对两个问题的概率;
恰好答对两个问题的概率;
(2)设 答对题数为
答对题数为 ,
, 答对题数为
答对题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
 ,
, 两名学生中间产生,该班委设计了一个测试方案:
两名学生中间产生,该班委设计了一个测试方案: ,
, 两名学生各自从6个问题中随机抽取3个问题作答,已知这6个问题中,学生
两名学生各自从6个问题中随机抽取3个问题作答,已知这6个问题中,学生 能正确回答其中的4个问题,而学生
能正确回答其中的4个问题,而学生 能正确回答每个问题的概率均为
能正确回答每个问题的概率均为 ,
, ,
, 两名学生对每个问题回答正确与否都是相互独立、互不影响的.
两名学生对每个问题回答正确与否都是相互独立、互不影响的.(1)求
 恰好答对两个问题的概率;
恰好答对两个问题的概率;(2)设
 答对题数为
答对题数为 ,
, 答对题数为
答对题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
您最近一年使用:0次
2021-09-04更新
|
183次组卷
|
2卷引用:福建省安溪八中、俊民中学、沼涛中学三校2020-2021学年高二下学期期中联考数学试题