名校
解题方法
1 . 新冠疫情不断反弹,各大商超多措并举确保市民生活货品不断档,超市员工加班加点工作.某大型超市为答谢各位员工一年来的锐意进取和辛勤努力,拟在年会后,通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有5种面值奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的5种面值的奖券中有2张面值为100元,其余3张均为50元,试比较员工获得100元奖励额与获得150元奖励额的概率的大小;
(2)公司对奖励总额的预算是7万元,预定箱子中所装的5种面值的奖券有两种方案:第一方案是3张面值30元和2张面值130元;第二方案是3张面值50元和2张面值100元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2023-04-14更新
|
721次组卷
|
9卷引用:山东省德州市2022-2023学年高二上学期期末数学试题
山东省德州市2022-2023学年高二上学期期末数学试题(已下线)模块一 专题2 概率统计 (人教B)(已下线)模块三 专题5 概率与统计--拔高能力练(人教B版)福建省宁德市寿宁县第一中学2022-2023学年高二下学期第二阶段考试(5月)数学试题江苏省连云港高级中学2022-2023学年高二下学期期中数学试题(已下线)拓展二:离散型随机变量的分布列与数字特征11种常见考法归类(2)(已下线)第10讲 离散型随机变量的均值与方差-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题03 条件概率与全概率公式(3)(已下线)高二下学期期末复习解答题压轴题二十二大题型专练(5)
名校
2 . 某公司全年圆满完成预定的生产任务,为答谢各位员工一年来的锐意进取和辛勤努力,公司决定在联欢晚会后,拟通过摸球兑奖的方式对500位员工进行奖励,规定:每位员工从一个装有4种面值的奖券的箱子中,一次随机摸出2张奖券,奖券上所标的面值之和就是该员工所获得的奖励额.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
(1)若箱子中所装的4种面值的奖券中有1张面值为80元,其余3张均为40元,试比较员工获得80元奖励额与获得120元奖励额的概率的大小;
(2)公司对奖励总额的预算是6万元,预定箱子中所装的4种面值的奖券有两种方案:第一方案是2张面值20元和2张面值100元;第二方案是2张面值40元和2张面值80元.为了使员工得到的奖励总额尽可能地符合公司的预算且每位员工所获得的奖励额相对均衡,请问选择哪一种方案比较好?并说明理由.
您最近一年使用:0次
2022-02-27更新
|
2368次组卷
|
10卷引用:第07讲 离散型随机变量及其分布列和数字特征 (精讲)
(已下线)第07讲 离散型随机变量及其分布列和数字特征 (精讲)上海市延安中学2023届高三下学期开学考试数学试题(已下线)第七章 随机变量及其分布 全章总结 (精讲)(2)上海市曹杨第二中学2023届高三三模数学试题山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题(已下线)技巧04 解答题解法与技巧(练)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》重庆市万州第二高级中学2021-2022学年高二下学期期中数学试题福建省厦门集美中学2021-2022学年高二下学期期中考试数学试题重庆市万州纯阳中学校2021-2022学年高二下学期期中数学(A卷)试题(已下线)第06讲 离散型随机变量的均值与方差(核心考点讲与练)-2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)
3 . 某公司举办公司员工联欢晩会,为活跃气氛,计划举行摸奖活动,有两种方案:
方案一:不放回从装有 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元:
元:
方案二:有放回从装有 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元,分别用随机变量
元,分别用随机变量 、
、 表示某员工按方案一和方案二抽奖的获奖金额.
表示某员工按方案一和方案二抽奖的获奖金额.
(1)求随机变量 的分布列和数学期望:
的分布列和数学期望:
(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选择哪种方案?请说明理由.
方案一:不放回从装有
 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元:
元:方案二:有放回从装有
 个红球和
个红球和 个白球的箱子中随机摸出
个白球的箱子中随机摸出 个球,每摸出一红球奖励
个球,每摸出一红球奖励 元,分别用随机变量
元,分别用随机变量 、
、 表示某员工按方案一和方案二抽奖的获奖金额.
表示某员工按方案一和方案二抽奖的获奖金额.(1)求随机变量
 的分布列和数学期望:
的分布列和数学期望:(2)用统计知识分析,为使公司员工获奖金额相对均衡,应选择哪种方案?请说明理由.
您最近一年使用:0次
2023-07-09更新
|
453次组卷
|
6卷引用:福建省南平市2022-2023学年高二下学期期末考试数学试题
福建省南平市2022-2023学年高二下学期期末考试数学试题(已下线)4.2.4 随机变量的数字特征(第2课时) 离散型随机变量的方差(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)模块二 专题3 概率与统计中决策问题(已下线)2023-2024学年高二下学期期中复习解答题压轴题十七大题型专练(2)(已下线)7.3.2 离散型随机变量的方差——课后作业(提升版)(已下线)专题04 随机变量的均值与方差综合--高二期末考点大串讲(人教B版2019选择性必修第二册)
4 . 为切实做好新冠疫情防控工作,有效、及时地控制和消除新冠肺炎的危害,增加学生对新冠肺炎预防知识的了解,某校举办了一次“新冠疫情”知识竞赛.竞赛分个人赛和团体赛两种.个人赛参赛方式为:组委会采取电脑出题的方式,从题库中随机出10道题,编号为 ,
, ,
, ,
, ,
, ,
,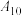 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
方案一:将班级选派的 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.
方案二:将班级选派的 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
 ,
, ,
, ,
, ,
, ,
,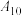 ,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:
,电脑依次出题,参赛选手按规则作答,每答对一道题得10分,答错得0分.团体赛以班级为单位,各班参赛人数必须为3的倍数,且不少于18人,团体赛分预赛和决赛两个阶段,其中预赛阶段各班可从以下两种参赛方案中任选一种参赛:方案一:将班级选派的
 名参赛选手每3人一组,分成
名参赛选手每3人一组,分成 组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这
组,电脑随机分配给同一组的3名选手一道相同的试题,3人均独立答题,若这3人中至少有2人回答正确,则该小组顺利出线;若这 个小组都顺利出线,则该班级晋级决赛.
个小组都顺利出线,则该班级晋级决赛.方案二:将班级选派的
 名参赛选手每
名参赛选手每 人一组,分成3组,电脑随机分配给同一组的
人一组,分成3组,电脑随机分配给同一组的 名选手一道相同的试题,每人均独立答题,若这
名选手一道相同的试题,每人均独立答题,若这 个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.
个人都回答正确,则该小组顺利出线;若这3个小组中至少有2个小组顺利出线,则该班级晋级决赛.(1)郭靖同学参加了个人赛,已知郭靖同学答对题库中每道题的概率均为
 ,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;
,每次作答结果相互独立,且他不会主动放弃任何一次作答机会,求郭靖同学得分的数学期望与方差;(2)在团体赛预赛中,假设A班每位参赛选手答对试题的概率均为常数
 ,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
,A班为使晋级团体赛决赛的可能性更大,应选择哪种参赛方式?请说明理由.
您最近一年使用:0次
名校
解题方法
5 . 某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
(1)若将频率视为概率,从这100个水果中有放回地随机抽取5个,求恰好有2个水果是礼品果的概率(结果用分数表示);
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,单价为21元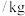 ;
;
方案2:分类卖出,分类后的水果售价如下:
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取3个, 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求 的分布列及方差
的分布列及方差 .
.
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考,
方案1:不分类卖出,单价为21元
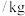 ;
;方案2:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元 | 16 | 18 | 22 | 24 |
(3)用分层抽样的方法从这100个水果中抽取10个,再从抽取的10个水果中随机抽取3个,
 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求 的分布列及方差
的分布列及方差 .
.
您最近一年使用:0次
6 . 在全球关注的抗击“新冠肺炎”中,某跨国科研中心的一个团队,研制了甲、乙两种治疗“新冠肺炎”新药,希望知道哪种新药更有效,为此进行动物试验,试验方案如下:
第一种:选取 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
第二种:选取 ,
, ,
, ,
, ,
, ,
, ,
,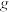 ,
, ,
, ,
, 共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,求其中服药有效的只数不超过2只的概率;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有90%变为正常白鼠,但正常白鼠仍有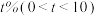 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为 .
.
(ⅰ)求 并写出
并写出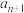 与
与 的关系式;
的关系式;
(ⅱ)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数 的值.
的值.
第一种:选取
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, 共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;
共10只患病白鼠,服用甲药后某项指标分别为:84,87,89,91,92,92,86,89,90,90;第二种:选取
 ,
, ,
, ,
, ,
, ,
, ,
,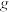 ,
, ,
, ,
, 共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;
共10只患病白鼠,服用乙药后某项指标分别为:81,87,83,82,80,90,86,89,84,79;该团队判定患病白鼠服药后这项指标不低于85的确认为药物有效,否则确认为药物无效.
(1)已知第一种试验方案的10个数据的平均数为89,求这组数据的方差;
(2)现需要从已服用乙药的10只白鼠中随机抽取7只,求其中服药有效的只数不超过2只的概率;
(3)该团队的另一实验室有1000只白鼠,其中900只为正常白鼠,100只为患病白鼠,每用新研制的甲药给所有患病白鼠服用一次,患病白鼠中有90%变为正常白鼠,但正常白鼠仍有
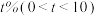 变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用
变为患病白鼠,假设实验室的所有白鼠都活着且数量不变,且记服用 次甲药后此实验室正常白鼠的只数为
次甲药后此实验室正常白鼠的只数为 .
.(ⅰ)求
 并写出
并写出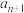 与
与 的关系式;
的关系式;(ⅱ)要使服用甲药两次后,该实验室正常白鼠至少有950只,求最大的正整数
 的值.
的值.
您最近一年使用:0次
名校
7 . 2023年五一劳动节前夕,某公司为全体员工发放奖励,奖励拟采用抽签方式发放:每位员工分别从标有不同面值的4张卡片中随机取出2张,2张卡片上的面值之和即为该员工的奖励金额.
(1)若4张卡片上的面值分别为100元,100元,300元,500元.
①求每位员工所获得的奖励金额不低于500元的概率;
②记每位员工所获得的奖励金额为X元,求X的分布列与期望;
(2)你能否设计一种抽签方案,使得4张卡片上的面值分别为100元,200元,300元,400元,500元中的3个,且每位员工所获得的奖励金额的期望值不变,且奖励金额相对均衡(只需给出一种方案并说明理由即可,不需要判断是否还有其他方案).
(1)若4张卡片上的面值分别为100元,100元,300元,500元.
①求每位员工所获得的奖励金额不低于500元的概率;
②记每位员工所获得的奖励金额为X元,求X的分布列与期望;
(2)你能否设计一种抽签方案,使得4张卡片上的面值分别为100元,200元,300元,400元,500元中的3个,且每位员工所获得的奖励金额的期望值不变,且奖励金额相对均衡(只需给出一种方案并说明理由即可,不需要判断是否还有其他方案).
您最近一年使用:0次
名校
解题方法
8 . 某校设计了一个实验学科的实验考查方案;考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作,规定:至少正确完成两题便可通过,已知6道备选题中甲生有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是 ,求:
,求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
 ,求:
,求:(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
您最近一年使用:0次
9 . 某人欲投资10万元,有两种方案可供选择.设X表示方案一所得收益(单位:万元),Y表示方案二所得收益(单位:万元).其分布列分别为:
假定同期银行利率为1.75%,该人征求你的意见,你通过分析会得到怎样的结论呢?
| X | −2 | 8 |
| P | 0.7 | 0.3 |
| Y | −3 | 12 |
| P | 0.7 | 0.3 |
您最近一年使用:0次
2023-10-05更新
|
92次组卷
|
2卷引用:湘教版(2019)选择性必修第二册课本例题3.2.4离散型随机变量的方差
名校
解题方法
10 . 某校为了庆祝建校100周年,举行校园文化知识竞赛.某班经过层层选拔,还有最后一个参赛名额要在甲、乙两名学生中产生,该班设计了一个选拔方案:甲,乙两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生甲能正确回答其中的4个问题,而学生乙能正确回答每个问题的概率均为 .甲、乙两名学生对每个问题回答正确与否都是相互独立的.
.甲、乙两名学生对每个问题回答正确与否都是相互独立的.
(1)分别求甲、乙两名学生恰好答对2个问题的概率;
(2)设甲答对的题数为 ,乙答对的题数为
,乙答对的题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
 .甲、乙两名学生对每个问题回答正确与否都是相互独立的.
.甲、乙两名学生对每个问题回答正确与否都是相互独立的.(1)分别求甲、乙两名学生恰好答对2个问题的概率;
(2)设甲答对的题数为
 ,乙答对的题数为
,乙答对的题数为 ,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
您最近一年使用:0次
2023-11-25更新
|
1105次组卷
|
5卷引用:贵州省贵阳市五校2023届高三联合考试(四)数学(理)试题
贵州省贵阳市五校2023届高三联合考试(四)数学(理)试题辽宁省沈阳市第一二〇中学2023-2024学年高二上学期第四次质量监测数学试题(已下线)考点13 二项分布与超级几何分布 2024届高考数学考点总动员(已下线)专题21 概率与统计的综合运用(13大题型)(练习)(已下线)第五章 概率统计创新问题 专题一 概率统计决策问题 微点1 概率统计决策问题(一)【培优版】