1 . 如图,在棱长为4的正方体 中,
中, ,
, 分别为棱
分别为棱 ,
, 的中点,点
的中点,点 是棱
是棱 上的一点,则下列说法正确的是( )
上的一点,则下列说法正确的是( )
 中,
中, ,
, 分别为棱
分别为棱 ,
, 的中点,点
的中点,点 是棱
是棱 上的一点,则下列说法正确的是( )
上的一点,则下列说法正确的是( )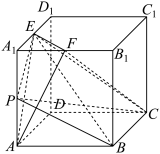
A.存在点 ,使得 ,使得 平面 平面 |
B.二面角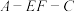 的余弦值为 的余弦值为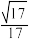 |
C.三棱锥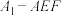 的内切球的体积为 的内切球的体积为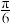 |
D. 的周长的最小值为 的周长的最小值为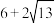 |
您最近一年使用:0次
2024-07-10更新
|
325次组卷
|
3卷引用:山西省大同市灵丘县豪洋中学2023-2024学年高一下学期期末考试数学试题
名校
解题方法
2 . 如图,在长方体 中,
中,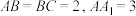 ,
, 为
为 的中点,
的中点, 为棱
为棱 上任意一点,直线
上任意一点,直线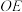 与棱
与棱 交于点
交于点 .则下列结论正确的是( )
.则下列结论正确的是( )
 中,
中,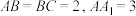 ,
, 为
为 的中点,
的中点, 为棱
为棱 上任意一点,直线
上任意一点,直线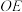 与棱
与棱 交于点
交于点 .则下列结论正确的是( )
.则下列结论正确的是( )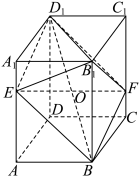
A.四边形 是平行四边形 是平行四边形 |
B.当 为 为 的中点时,四边形 的中点时,四边形 是菱形 是菱形 |
C.四边形 的周长的最小值为9 的周长的最小值为9 |
D.四棱锥 的体积为4 的体积为4 |
您最近一年使用:0次
2024-07-09更新
|
186次组卷
|
2卷引用:山西省大同市第一中学校、忻州市第一中学校2023-2024学年高一下学期7月期末考试数学试题
3 . 如图,在棱长均为1的平行六面体 中,
中,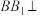 平面
平面 ,
, 分别是线段
分别是线段 和线段
和线段 上的动点,且满足
上的动点,且满足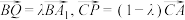 ,则下列说法正确的是( )
,则下列说法正确的是( )
 中,
中,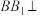 平面
平面 ,
, 分别是线段
分别是线段 和线段
和线段 上的动点,且满足
上的动点,且满足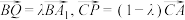 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.当 时, 时,   |
B.当 时,若 时,若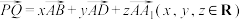 ,则 ,则 |
C.当 时,直线 时,直线 与直线 与直线 所成角的大小为 所成角的大小为 |
D.当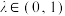 时,三棱锥 时,三棱锥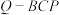 的体积的最大值为 的体积的最大值为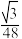 |
您最近一年使用:0次
2024-07-07更新
|
755次组卷
|
5卷引用:山西省太原市小店区山西百校联考2023-2024学年高二下学期7月期末考试数学试题
山西省太原市小店区山西百校联考2023-2024学年高二下学期7月期末考试数学试题河南省商丘市中州联盟2023-2024学年高二上学期期末考试数学试卷(已下线)压轴题01 空间向量和立体几何-【常考压轴题】(人教B版2019选择性必修第一册)辽宁省名校联盟2024-2025学年高二上学期第一次月考数学试卷陕西省咸阳市乾县第一中学2024-2025学年高二第二次阶段性检测数学试题
4 . 如图,矩形 中,
中, ,
, 为
为 的中点,将
的中点,将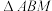 沿直线
沿直线 翻折至
翻折至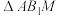 ,连接
,连接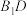 ,
, 为
为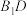 的中点,则在翻折过程中,下列结论正确的是( )
的中点,则在翻折过程中,下列结论正确的是( )
 中,
中, ,
, 为
为 的中点,将
的中点,将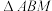 沿直线
沿直线 翻折至
翻折至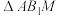 ,连接
,连接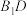 ,
, 为
为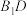 的中点,则在翻折过程中,下列结论正确的是( )
的中点,则在翻折过程中,下列结论正确的是( )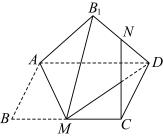
A. 的长是定值 的长是定值 |
B.存在某个位置,使得 |
C.存在某个位置,使得平面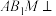 平面 平面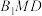 |
D.当三棱锥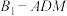 的体积取最大值时,其外接球的表面积是 的体积取最大值时,其外接球的表面积是 |
您最近一年使用:0次
5 . 在三棱锥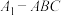 中,
中,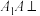 平面
平面 ,
,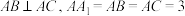 ,P为
,P为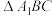 内的一个动点(包括边界),
内的一个动点(包括边界), 与平面
与平面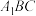 所成的角为
所成的角为 ,则( )
,则( )
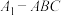 中,
中,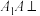 平面
平面 ,
,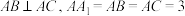 ,P为
,P为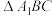 内的一个动点(包括边界),
内的一个动点(包括边界), 与平面
与平面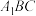 所成的角为
所成的角为 ,则( )
,则( )A.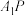 的最小值为 的最小值为 | B.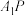 的最大值为 的最大值为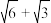 |
C.有且仅有一个点P,使得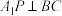 | D.所有满足条件的线段 形成的曲面面积 形成的曲面面积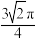 |
您最近一年使用:0次
2024-04-15更新
|
494次组卷
|
9卷引用:山西省朔州市怀仁市2023-2024学年高三上学期第二次教学质量调研数学试题
解题方法
6 . 已知正方体 的棱长为
的棱长为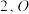 是空间中的一动点,下列结论正确的是( )
是空间中的一动点,下列结论正确的是( )
 的棱长为
的棱长为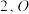 是空间中的一动点,下列结论正确的是( )
是空间中的一动点,下列结论正确的是( )A.若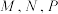 分别为 分别为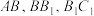 的中点,则 的中点,则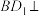 平面 平面 |
B.平面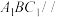 平面 平面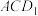 |
C.若 ,则 ,则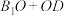 的最小值为 的最小值为 |
D.若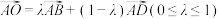 ,则平面 ,则平面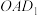 截正方体 截正方体 所得截面面积的最大值为 所得截面面积的最大值为 |
您最近一年使用:0次
解题方法
7 . 如图,矩形 中,
中, ,
, 为边
为边 的中点,将
的中点,将 沿
沿 翻折成
翻折成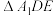 ,若
,若 为线段
为线段 的中点,则在翻折过程中,下列结论中正确的是( )
的中点,则在翻折过程中,下列结论中正确的是( )

 中,
中, ,
, 为边
为边 的中点,将
的中点,将 沿
沿 翻折成
翻折成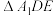 ,若
,若 为线段
为线段 的中点,则在翻折过程中,下列结论中正确的是( )
的中点,则在翻折过程中,下列结论中正确的是( )
A.翻折到某个位置,使得 |
B.翻折到某个位置,使得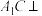 平面 平面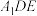 |
C.四棱锥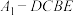 体积的最大值为 体积的最大值为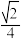 |
D.点 在某个球面上运动 在某个球面上运动 |
您最近一年使用:0次
名校
解题方法
8 . 如图,棱长为2的正方体 中,E,F分别为棱
中,E,F分别为棱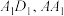 的中点,G为线段
的中点,G为线段 上的动点,则( )
上的动点,则( )
 中,E,F分别为棱
中,E,F分别为棱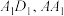 的中点,G为线段
的中点,G为线段 上的动点,则( )
上的动点,则( )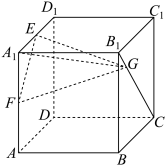
A.三棱锥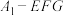 的体积为定值 的体积为定值 |
B.存在点G,使得 平面EFG 平面EFG |
C.G为 中点时,直线EG与 中点时,直线EG与 所成角最小 所成角最小 |
D.点F到直线EG距离的最小值为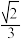 |
您最近一年使用:0次
2024-02-05更新
|
497次组卷
|
5卷引用:山西省运城市2023-2024学年高二上学期期末调研测试数学试题
山西省运城市2023-2024学年高二上学期期末调研测试数学试题(已下线)第二章 立体几何中的计算 专题七 空间范围与最值问题 微点7 角度的范围与最值问题(二)【基础版】广西壮族自治区南宁市广西大学附属中学2023-2024学年高二下学期4月月考数学试题(已下线)专题2 空间向量解决立体几何中最值问题【练】(高二期中压轴专项)广西南宁市第十四中学2024-2025学年高二上学期9月月考数学试卷
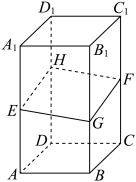
9 . 如图,在正四棱柱 中,
中, ,
,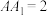 ,E,F分别是棱
,E,F分别是棱 ,
, 的中点,过点E,F的平面分别与棱
的中点,过点E,F的平面分别与棱 ,
, 交于点G,H,则下列说法正确的是( )
交于点G,H,则下列说法正确的是( )
 中,
中, ,
,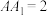 ,E,F分别是棱
,E,F分别是棱 ,
, 的中点,过点E,F的平面分别与棱
的中点,过点E,F的平面分别与棱 ,
, 交于点G,H,则下列说法正确的是( )
交于点G,H,则下列说法正确的是( )
A.四边形 的面积的最小值为1 的面积的最小值为1 |
B.平面 与平面 与平面 所成角的最大值为 所成角的最大值为 |
C.四棱锥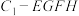 的体积为定值 的体积为定值 |
D.点 到平面 到平面 的距离的最大值为 的距离的最大值为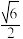 |
您最近一年使用:0次
解题方法
10 . 在棱长为1的正方体 中,
中, 为线段
为线段 的中点,点
的中点,点 和
和 分别满足
分别满足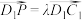 ,
, ,其中
,其中 ,
,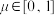 ,则下列结论正确的是( )
,则下列结论正确的是( )
 中,
中, 为线段
为线段 的中点,点
的中点,点 和
和 分别满足
分别满足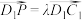 ,
, ,其中
,其中 ,
,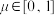 ,则下列结论正确的是( )
,则下列结论正确的是( )A.当 时,三棱锥 时,三棱锥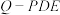 的体积为定值 的体积为定值 |
B.当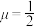 时,四棱锥 时,四棱锥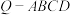 的外接球的表面积是 的外接球的表面积是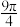 |
C.当 时,不存在 时,不存在 使得 使得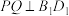 |
D. 的最小值为 的最小值为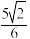 |
您最近一年使用:0次



