1 . 设函数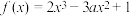 ,则( )
,则( )
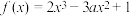 ,则( )
,则( )A.当 时, 时, 有三个零点 有三个零点 |
B.当 时, 时, 是 是 的极大值点 的极大值点 |
C.存在a,b,使得 为曲线 为曲线 的对称轴 的对称轴 |
D.存在a,使得点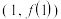 为曲线 为曲线 的对称中心 的对称中心 |
您最近一年使用:0次
2024-06-07更新
|
25359次组卷
|
28卷引用:福建省泉州市2025届高中毕业班模拟检测(一)数学试题
福建省泉州市2025届高中毕业班模拟检测(一)数学试题2024年新课标全国Ⅱ卷数学真题(已下线)2024年高考数学真题完全解读(新高考Ⅱ卷)专题03导数及其应用(已下线)2024年新课标全国Ⅱ卷数学真题变式题11-15(已下线)高二数学期末模拟试卷01【好题汇编】-备战2023-2024学年高二数学下学期期末真题分类汇编(北师大版2019选择性必修第二册)(已下线)五年新高考专题09导数及其应用(已下线)三年新高考专题09导数及其应用(已下线)第03讲 导数与函数的极值、最值(七大题型)(讲义)福建省福州第二中学2023-2024学年高二下学期期末测试数学试卷(已下线)3.3 利用导数研究函数的极值与最值(已下线)专题05 函数的概念与性质(4大考向真题解读)(已下线)重难点专题 2-2 三次函数图像与性质【10类题型】广东省广州市番禺区2023-2024学年高二下学期期末教学质量监测数学试题(已下线)周测8 导数在不等式、函数零点等综合应用(提升卷)(已下线)数学01(新九省地区专用)-2025届新高三开学摸底考试卷湖北省十堰市郧阳区第一中学2023-2024学年5月月考数学试题新疆石河子第一中学2024-2025学年高三上学期开学考试数学试题湖南省平江县颐华高级中学2024-2025学年高三上学期入学考试数学试题湖南省长沙市明德中学2024-2025学年高三上学期8月阶段检测数学试卷福建省宁德市古田县第一中学2024-2025学年高三第一次模拟考试数学试卷福建省建瓯市芝华中学2024-2025学年高三上学期第一次月考数学试题陕西省西安市第八十九中学教育集团弘德中学2023-2024学年高二下学期适应性演练考试数学试题云南省昆明市第九中学2025届高三上学期开学质量监测数学试题福建省福州黎明中学2025届高三上学期9月月考数学试题山东省济宁市实验中学2025届高三上学期10月月考数学试题福建省福州第一中学2025届高三上学期10月月考数学试题河北省保定市部分地区2024-2025学年高三上学期9月模拟考试数学试卷
2 . 拉格朗日中值定理是微分学的基本定理之一,定理内容如下:如果函数 在闭区间
在闭区间 上的图象连续不间断,在开区间
上的图象连续不间断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内至少存在一点
内至少存在一点 ,使得
,使得 成立,其中
成立,其中 叫做
叫做 在
在 上的“拉格朗日中值点”.根据这个定理,可得函数
上的“拉格朗日中值点”.根据这个定理,可得函数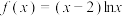 在
在 上的“拉格朗日中值点”的个数为( )
上的“拉格朗日中值点”的个数为( )
 在闭区间
在闭区间 上的图象连续不间断,在开区间
上的图象连续不间断,在开区间 内的导数为
内的导数为 ,那么在区间
,那么在区间 内至少存在一点
内至少存在一点 ,使得
,使得 成立,其中
成立,其中 叫做
叫做 在
在 上的“拉格朗日中值点”.根据这个定理,可得函数
上的“拉格朗日中值点”.根据这个定理,可得函数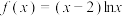 在
在 上的“拉格朗日中值点”的个数为( )
上的“拉格朗日中值点”的个数为( )| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
2023-02-17更新
|
1502次组卷
|
16卷引用:福建省泉州市泉港区第二中学2023-2024学年高二下学期3月月考数学试题
福建省泉州市泉港区第二中学2023-2024学年高二下学期3月月考数学试题山西省忻州市河曲县中学校2022-2023学年高二下学期开学考试数学试题山西省名校2022-2023学年高二下学期联考数学试题云南省昆明市安宁中学2022-2023学年高二下学期第一次检测数学试题陕西省商洛市2022-2023学年高二上学期期末文科数学试题广东省佛山市南海区石门中学2022-2023学年高二下学期第一次质量检测数学试题(已下线)第五章 一元函数的导数及其应用(单元综合检测)广东省珠海市第一中学2022-2023学年高二下学期3月月考数学试题(已下线)模块五 专题2 全真能力模拟(高二人教B)广东省佛山市南海区2022-2023学年高二下学期期中数学试题河北省廊坊市固安县马庄中学等2校2022-2023学年高二下学期开学考试数学试题山东省临沂市郯城第一中学2023-2024学年高二下学期阶段性检测一数学试卷吉林省长春市第八中学2023-2024学年高二下学期第一次月考数学试题(已下线)核心考点3 导数的应用(恒成立,不等式,零点) A基础卷 (高二期末考试必考的10大核心考点)(已下线)第三章 第五节 导数与函数零点【同步课时】基础卷(已下线)周测8 导数在不等式、函数零点等综合应用(基础卷)
3 . 已知函数 ,若
,若 有两个零点,则a的取值范围是( )
有两个零点,则a的取值范围是( )
 ,若
,若 有两个零点,则a的取值范围是( )
有两个零点,则a的取值范围是( )A.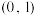 | B.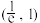 | C. | D.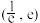 |
您最近一年使用:0次
2023-07-27更新
|
993次组卷
|
8卷引用:福建省安溪第八中学2023-2024学年高二下学期6月份质量检测数学试题
福建省安溪第八中学2023-2024学年高二下学期6月份质量检测数学试题广东省韶关市2022-2023学年高二下学期期末数学试题广东省广州市第一中学2024届高三上学期10月月考数学试题(已下线)第09讲:一元函数的导数及其应用 (必刷7大考题+7大题型) -2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)(已下线)第10讲:导数期末题型突破(单调性、不等式、零点、恒成立)(已下线)高二数学下学期期末考点大通关真题必刷100题(2) --高二期末考点大串讲(人教B版2019选择性必修第二册)浙江省台州十校联盟2023-2024学年高二下学期4月期中联考数学试题(已下线)专题12 函数单调性 导数的符号(经典好题母题)【练】
名校
4 . 如图,在 中,
中, ,
,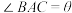 ,
,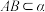 ,设点
,设点 在
在 上的射影为
上的射影为 ,将
,将 绕边
绕边 任意转动,则有( )
任意转动,则有( )

 中,
中, ,
,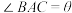 ,
,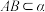 ,设点
,设点 在
在 上的射影为
上的射影为 ,将
,将 绕边
绕边 任意转动,则有( )
任意转动,则有( )
A.若 为锐角,则在转动过程中存在位置使 为锐角,则在转动过程中存在位置使 |
B.若 为直角,则在转动过程中存在位置使 为直角,则在转动过程中存在位置使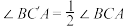 |
C.若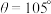 ,则在转动过程中存在位置使 ,则在转动过程中存在位置使 |
D.若 ,则在转动过程中存在位置使 ,则在转动过程中存在位置使 |
您最近一年使用:0次
2022-07-07更新
|
1904次组卷
|
5卷引用:福建省南安市龙泉中学2023届高三A班上学期数学(理)试题(7)
名校
解题方法
5 . 已知 .
.
(1)若函数 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(2)若函数 有两个极值点
有两个极值点 ,证明:
,证明: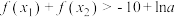 .
.
 .
.(1)若函数
 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;(2)若函数
 有两个极值点
有两个极值点 ,证明:
,证明: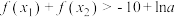 .
.
您最近一年使用:0次
2022-11-27更新
|
1321次组卷
|
7卷引用:福建省永春第一中学2022-2023学年高二下学期6月月考数学试题
福建省永春第一中学2022-2023学年高二下学期6月月考数学试题广东省广州市2023届高三上学期11月调研数学试题江西省新余市2023届高三上学期期末质量检测数学(文)试题(已下线)专题17 函数与导数压轴解答题常考套路归类(精讲精练)-3(已下线)江苏省八市2023届高三二模数学试题变式题17-22山东省济南市济阳闻韶中学2023届高三上学期12月月考数学试题(已下线)专题突破卷10 导数与不等式证明
6 . 关于函数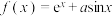 ,
,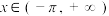 ,下列说法正确的是( )
,下列说法正确的是( )
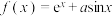 ,
,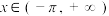 ,下列说法正确的是( )
,下列说法正确的是( )A.当 时, 时, 在 在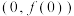 处的切线方程为 处的切线方程为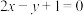 |
B.当 时, 时, 存在唯一极小值点 存在唯一极小值点 且 且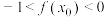 |
C.对任意 , , 在 在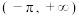 上均存在零点 上均存在零点 |
D.存在 , , 在 在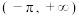 上有且只有一个零点 上有且只有一个零点 |
您最近一年使用:0次
2022-11-13更新
|
1080次组卷
|
25卷引用:福建省石狮市永宁中学2023届高三第四次模拟数学试题
福建省石狮市永宁中学2023届高三第四次模拟数学试题2020届山东省烟台市高考诊断性测试(4月)数学试题江苏省扬州中学2019-2020学年高二下学期期中数学试题山东师范大学附属中学2020届高三最后一卷(打靶卷)数学试题山东师范大学附属中学2020届高三6月模拟检测数学试题江苏省苏州大学附中2019-2020学年高二下学期6月阶段调研数学试题(已下线)考点15 导数的概念及运算(考点专练)-备战2021年新高考数学一轮复习考点微专题辽宁省锦州市2019-2020学年高二(下)期末数学试题广东省清远市清新一中2021届高三上学期月测2数学试题湖南省邵阳市邵东市第一中学2020-2021学年高三上学期第五次月考数学试题(已下线)2021届高三数学新高考“8+4+4”小题狂练(42)(已下线)2021届高三数学新高考“8+4+4”小题狂练(45)江苏省盐城市滨海中学2020-2021学年高三上学期迎八省联考考前热身数学试题(已下线)专题24 导数在研究函数中的应用(2)-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练(已下线)第04章《期中综合试卷二》(A卷基础篇)-2020-2021学年高二数学下学期同步单元AB卷(苏教版)江苏省苏州市第一中学2020-2021学年高二下学期期中数学试题广东省广州市真光中学2020-2021学年高二下学期期中数学试题江苏省无锡市宜兴市张渚高级中学2020-2021学年高二下学期3月月考数学试题江苏苏州市相城区陆慕高级中学2020-2021学年高二下学期4月月考数学试题江苏省常州市武进区礼嘉中学2020-2021学年高二下学期第二次阶段质量调研数学试题广东省揭阳市普宁市华侨中学2023届高三上学期11月期中数学试题重庆市永川北山中学校2022届高三高考预测二数学试题(已下线)广东省江门市棠下中学2022-2023学年高三上学期数学试题变式题11-16(已下线)5.3.2函数的极值与最大(小)值(同步练习)辽宁省大连市第八中学2020-2021学年高三上学期12月月考数学试题
7 . 对于正整数n,设 是关于x的方程:
是关于x的方程: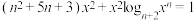 的实根,记
的实根,记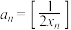 ,其中
,其中 表示不超过x的最大整数,则
表示不超过x的最大整数,则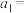
______ ;若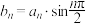 ,
, 为
为 的前n项和,则
的前n项和,则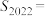
______ .
 是关于x的方程:
是关于x的方程: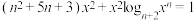 的实根,记
的实根,记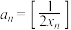 ,其中
,其中 表示不超过x的最大整数,则
表示不超过x的最大整数,则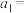
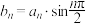 ,
, 为
为 的前n项和,则
的前n项和,则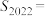
您最近一年使用:0次
2022-03-06更新
|
1297次组卷
|
8卷引用:福建省永春第一中学2022-2023学年高二上学期期末考试数学试题
福建省永春第一中学2022-2023学年高二上学期期末考试数学试题黑龙江省哈尔滨市第三中学2021-2022学年高三第一次模拟数学(理科)试题(已下线)思想04 化归与转化思想(练)--第三篇 思想方法篇-《2022年高考数学二轮复习讲练测(浙江专用)》(已下线)思想04 化归与转化思想(练)--第三篇 思想方法篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》山东省青岛市青岛第二中学2022-2023学年高二上学期期末数学试题(已下线)期末真题必刷压轴60题(22个考点专练)-【满分全攻略】2023-2024学年高二数学同步讲义全优学案(沪教版2020必修第三册)(已下线)第1题 高斯函数与数列最值结合(压轴小题6月)(已下线)【练】专题10 数列与其它知识的交汇问题
8 . 若函数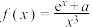 在
在 上存在极值,则
上存在极值,则 的取值范围为
的取值范围为______ .
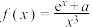 在
在 上存在极值,则
上存在极值,则 的取值范围为
的取值范围为
您最近一年使用:0次
2023-01-30更新
|
456次组卷
|
3卷引用:福建省泉州市永春二中、平山中学等五校2022-2023学年高二下学期期中联考数学试题
名校
9 . 关于函数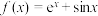 ,
, ,下列四个结论中正确的为
,下列四个结论中正确的为__________ .
① 在
在 上单调递减,在
上单调递减,在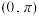 上单调递增;
上单调递增;
② 有两个零点;
有两个零点;
③ 存在唯一极小值点
存在唯一极小值点 ,且
,且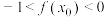 ;
;
④ 有两个极值点.
有两个极值点.
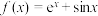 ,
, ,下列四个结论中正确的为
,下列四个结论中正确的为①
 在
在 上单调递减,在
上单调递减,在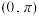 上单调递增;
上单调递增; ②
 有两个零点;
有两个零点;③
 存在唯一极小值点
存在唯一极小值点 ,且
,且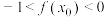 ;
; ④
 有两个极值点.
有两个极值点.
您最近一年使用:0次
2022-03-31更新
|
985次组卷
|
8卷引用:福建省泉州市晋江二中、鹏峰中学、广海中学、泉港五中2023届高三上学期10月期中联考数学试题
福建省泉州市晋江二中、鹏峰中学、广海中学、泉港五中2023届高三上学期10月期中联考数学试题河南省南阳市第一中学2021-2022学年高二下学期第一次月考理科数学试题四川省自贡市富顺第二中学校2021-2022学年高二下学期5月月考数学(文)试题四川省自贡市富顺第二中学校2021-2022学年高二下学期5月月考数学(理)试题2022届黑龙江省大庆实验中学实验二部高考得分训练数学理科试卷二(5月模拟二)(已下线)专题08 导数及其应用(模拟练)湖北省十堰市东风高级中学2021-2022学年高二下学期期中数学试题(已下线)第九章 导数与三角函数的联袂 专题二 导数法求含三角函数的函数极值与最值 微点3 导数法求含三角函数的函数极值与最值综合训练
名校
解题方法
10 . 已知 为方程
为方程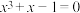 的根,
的根, 为方程
为方程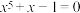 的根,则( )
的根,则( )
 为方程
为方程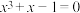 的根,
的根, 为方程
为方程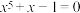 的根,则( )
的根,则( )A.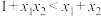 | B. |
C. | D. |
您最近一年使用:0次
2024-05-24更新
|
637次组卷
|
5卷引用:福建省泉州市安溪第一中学2023-2024学年高二下学期5月份质量检测数学试题



