2022·广西贵港·三模
名校
解题方法
1 . 已知曲线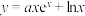 在点
在点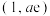 处的切线方程为
处的切线方程为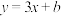 ,则( )
,则( )
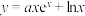 在点
在点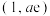 处的切线方程为
处的切线方程为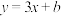 ,则( )
,则( )A. , , | B. , , |
C.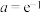 , , | D.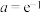 , , |
您最近一年使用:0次
2022-05-26更新
|
2962次组卷
|
17卷引用:第39练 导数的概念、意义及运算
(已下线)第39练 导数的概念、意义及运算四川省泸州市泸县教育共同体2023届高三一诊模拟考试数学(理)试题四川省泸州市泸县教育共同体2023届高三一诊模拟考试数学(文)试题河南省2023届普通高中毕业班高考适应性考试文科数学试题(已下线)专题14 导数的概念与运算-2四川省泸县第一中学2023届高三三诊模拟考试理科数学试题四川省泸县第一中学2023届高三三诊模拟考试文科数学试题(已下线)专题04 导数及其应用-2云南省昆明市云南师范大学附属中学2024届高三上学期期初开学数学试题(已下线)专题3.1 导数的概念及其几何意义与运算【八大题型】广西贵港市高级中学2022届高三毕业班5月模拟考试数学(理)试题江西省宜春市铜鼓中学2021-2022学年高二下学期期末质量检测数学(文)试题江苏省盐城市响水中学2022-2023学年高二创新班上学期10月月考数学试题(已下线)广东省深圳市深圳中学2024届高三上学期8月开学摸底数学试题广东省佛山市高明区第一中学2022-2023学年高二下学期3月教学质量检测数学试题广东省佛山市顺德区华侨中学2024届高三上学期8月月考数学试题宁夏回族自治区石嘴山市平罗中学2024届高三下学期第三次模拟考试数学(文)试题
名校
解题方法
2 .  是定义在
是定义在 上的函数,
上的函数, 是
是 的导函数,已知
的导函数,已知 ,且
,且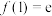 ,则不等式
,则不等式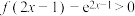 的解集为( )
的解集为( )
 是定义在
是定义在 上的函数,
上的函数, 是
是 的导函数,已知
的导函数,已知 ,且
,且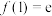 ,则不等式
,则不等式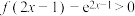 的解集为( )
的解集为( )A.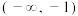 | B. |
C. | D.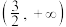 |
您最近一年使用:0次
2022-05-26更新
|
920次组卷
|
6卷引用:四川省内江市第六中学2021-2022学年高二下学期期中文科数学试题
四川省内江市第六中学2021-2022学年高二下学期期中文科数学试题四川省绵阳市开元中学2021-2022学年高二下学期半期质量检测理科数学试题(已下线)专题03 原函数与导函数混合还原问题-1四川省成都市石室中学2021-2022学年高二下学期零诊模拟练习文科数学试题江苏省南通市通州区金沙中学2021-2022学年高二下学期6月调研考试数学试题(已下线)高二数学下学期第二次月考模拟试卷(选择性必修第二册,含数列和导数)-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)
名校
解题方法
3 . 若曲线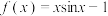 在
在 处的切线与直线
处的切线与直线 互相垂直,则( )
互相垂直,则( )
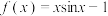 在
在 处的切线与直线
处的切线与直线 互相垂直,则( )
互相垂直,则( )A.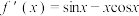 | B.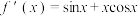 |
C.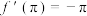 | D. |
您最近一年使用:0次
2022-05-26更新
|
903次组卷
|
6卷引用:吉林省长春市第二实验中学2021-2022学年高二下学期期中考试数学试题
吉林省长春市第二实验中学2021-2022学年高二下学期期中考试数学试题(已下线)专题08导数的概念、运算与几何意义-2022年新高三数学暑假自学课精讲精练(已下线)专题13 导数的定义、运算与几何意义山东省菏泽市定陶区明德学校(山大附中实验学校)2022-2023学年高二下学期创新部第一次月考数学试题河北省秦皇岛市青龙满族自治县实验中学2023届高三上学期期末数学试题(已下线)专题1.5 导数与切线方程(强化训练)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
4 . 定义在区间 上的连续函数
上的连续函数 导函数为
导函数为 ,若
,若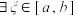 使得
使得 ,则称
,则称 为区间
为区间 上的“中值点”.下列在区间
上的“中值点”.下列在区间 上“中值点”多于一个的函数是( )
上“中值点”多于一个的函数是( )
 上的连续函数
上的连续函数 导函数为
导函数为 ,若
,若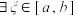 使得
使得 ,则称
,则称 为区间
为区间 上的“中值点”.下列在区间
上的“中值点”.下列在区间 上“中值点”多于一个的函数是( )
上“中值点”多于一个的函数是( )A. | B. |
C. | D.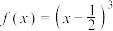 |
您最近一年使用:0次
2022-05-24更新
|
302次组卷
|
3卷引用:广东省广州南洋英文学校2021-2022学年高二下学期期中数学试题
2022·江苏苏州·模拟预测
解题方法
5 . 已知奇函数 在点
在点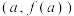 处的切线方程为
处的切线方程为 ,则
,则 ( )
( )
 在点
在点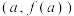 处的切线方程为
处的切线方程为 ,则
,则 ( )
( )A. 或1 或1 | B.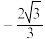 或 或 | C. 或2 或2 | D.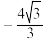 或 或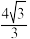 |
您最近一年使用:0次
2022-05-24更新
|
836次组卷
|
4卷引用:4.1 切线方程(精练)-【一隅三反】2023年高考数学一轮复习(提升版)(新高考地区专用)
(已下线)4.1 切线方程(精练)-【一隅三反】2023年高考数学一轮复习(提升版)(新高考地区专用)(已下线)专题14 导数的概念与运算-2山西省临汾市洪洞县向明中学2024届高三上学期第四次考试(半月考)数学试题江苏省苏州市2022届高三下学期高考前模拟数学试题
名校
6 . 求下列各函数的导数:
(1)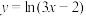 ;
;
(2)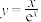 ;
;
(3)
(1)
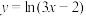 ;
;(2)
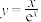 ;
;(3)

您最近一年使用:0次
7 . 函数 的导函数是( )
的导函数是( )
 的导函数是( )
的导函数是( )A.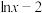 | B. | C.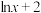 | D. |
您最近一年使用:0次
名校
8 . 设函数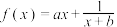 (
( ,
,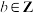 ),曲线
),曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求 ;
;
(2)求函数 的解析式.
的解析式.
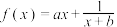 (
( ,
,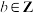 ),曲线
),曲线 在点
在点 处的切线方程为
处的切线方程为 .
.(1)求
 ;
;(2)求函数
 的解析式.
的解析式.
您最近一年使用:0次
2022-05-21更新
|
1717次组卷
|
3卷引用:天津市第四十二中学2021-2022学年高二下学期期中数学试题
21-22高二下·广西柳州·阶段练习
名校
解题方法
9 . 曲线 上的点到直线
上的点到直线 的距离的最小值为( )
的距离的最小值为( )
 上的点到直线
上的点到直线 的距离的最小值为( )
的距离的最小值为( )A. | B. |
C.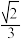 | D.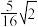 |
您最近一年使用:0次
2022·湖北宜昌·模拟预测
名校
10 . 函数 的图像在点
的图像在点 处的切线方程为
处的切线方程为_________ .
 的图像在点
的图像在点 处的切线方程为
处的切线方程为
您最近一年使用:0次



