1 . 某数学兴趣小组为测量一古建筑物的高度,设计了测算方案.如图,在该建筑物旁水平地面上共线的三点A,B,C处测得其顶点M的仰角分别为 ,
, ,
, ,且
,且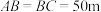 ,则该古建筑的高度为( )
,则该古建筑的高度为( )
 ,
, ,
, ,且
,且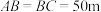 ,则该古建筑的高度为( )
,则该古建筑的高度为( )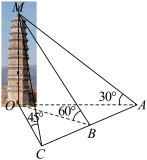
A. | B.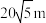 | C. | D. |
您最近一年使用:0次
2024-08-16更新
|
565次组卷
|
4卷引用:安徽省宣城中学2024-2025学年高二上学期开学测试数学试题
安徽省宣城中学2024-2025学年高二上学期开学测试数学试题四川省绵阳市2023-2024学年高一下学期期末考试数学试题四川省内江市第一中学2024-2025学年高二上学期开学考试数学试题(已下线)第4题 解三角形的实际应用(高三备考11月刊)
2 . 中国古代四大名楼鹳雀楼,位于山西省运城市永济市蒲州镇,因唐代诗人王之涣的诗作《登鹳雀楼》而流芳后世.如图,某同学为测量鹳雀楼的高度MN,在鹳雀楼的正东方向找到一座建筑物AB,高约为37m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A,鹳雀楼顶部M的仰角分别为 和
和 ,在A处测得楼顶部M的仰角为
,在A处测得楼顶部M的仰角为 ,则鹳雀楼的高度约为( )
,则鹳雀楼的高度约为( )
 和
和 ,在A处测得楼顶部M的仰角为
,在A处测得楼顶部M的仰角为 ,则鹳雀楼的高度约为( )
,则鹳雀楼的高度约为( )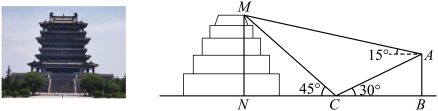
| A.74m | B.60m | C.52m | D.91m |
您最近一年使用:0次
2023-09-04更新
|
2066次组卷
|
23卷引用:安徽省亳州市第二完全中学2023-2024学年高二上学期开学质量检测数学试卷
安徽省亳州市第二完全中学2023-2024学年高二上学期开学质量检测数学试卷山西省省际名校2023届高三联考一(启航卷)数学试题(已下线)专题强化 正、余弦定理综合性问题讲与练(2)-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(苏教版2019必修第二册)江苏省泰州中学2022-2023学年高一下学期期中数学试题辽宁省大连市滨城高中联盟2022-2023学年高一下学期期中考试数学试题湖北省武汉市华中师范大学第一附属中学2022-2023学年高一下学期5月月考数学试题(已下线)第11章:解三角形 重点题型复习-【题型分类归纳】2022-2023学年高一数学同步讲与练(苏教版2019必修第二册)河南省许昌市2022-2023学年高一下学期期末数学试题福建省莆田锦江中学2022-2023学年高一下学期期中质检数学试题河南省开封市河大附中实验学校2022-2023学年高一下学期第一次月考数学试题辽宁省沈阳市新民市高级中学2023-2024学年高三上学期9月份开学考试数学试题湖南省益阳市安化县第二中学2022-2023学年高一下学期4月月考数学试题北京市第一六六中学2024届高三上学期9月阶段性诊断数学试题浙江省“南太湖”联盟2023-2024学年高二上学期第一次联考数学试题陕西省西安市长安区2023-2024学年高三上学期10月第三次月考理科数学试题河北省石家庄二十七中2023-2024学年高二上学期开学考数学试题内蒙古赤峰市赤峰二中2024届高三上学期10月月考数学(文)试题河北省石家庄二十二中2023-2024学年高二上学期第一次月考(10月)数学试题(已下线)专题13 余弦定理、正弦定理的应用-【寒假自学课】(苏教版2019)(已下线)6.4.3 课时3 余弦定理、正弦定理应用举例-同步题型分类归纳讲与练(人教A版2019必修第二册)(已下线)模块四期中重组篇辽宁(高一下人教B版)(已下线)【一题多变】三点共线 向量斜率江西师范大学附属中学2023-2024学年高一下学期5月数学素养测试卷
3 . 泰姬陵是印度在世界上知名度最高的古建筑之一,被列为“世界文化遗产”.秦姬陵是印度古代皇帝为了纪念他的皇妃建造的,于1631年开始建造,用时22年,距今已有366年历史.如图所示,为了估算泰姬陵的高度,现在泰姬陵的正东方向找一参照物 ,高约为
,高约为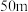 ,在它们之间的地面上的点Q(B,Q,D三点共线)处测得
,在它们之间的地面上的点Q(B,Q,D三点共线)处测得 处、泰姬陵顶端
处、泰姬陵顶端 处的仰角分别是
处的仰角分别是 和
和 ,在
,在 处测得泰姬陵顶端
处测得泰姬陵顶端 处的仰角为
处的仰角为 ,则估算泰姬陵的高度
,则估算泰姬陵的高度 为( )
为( )
 ,高约为
,高约为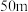 ,在它们之间的地面上的点Q(B,Q,D三点共线)处测得
,在它们之间的地面上的点Q(B,Q,D三点共线)处测得 处、泰姬陵顶端
处、泰姬陵顶端 处的仰角分别是
处的仰角分别是 和
和 ,在
,在 处测得泰姬陵顶端
处测得泰姬陵顶端 处的仰角为
处的仰角为 ,则估算泰姬陵的高度
,则估算泰姬陵的高度 为( )
为( )

A.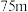 | B. | C.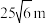 | D.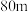 |
您最近一年使用:0次
2023-08-09更新
|
638次组卷
|
16卷引用:安徽省六安第一中学2023-2024学年高三上学期第二次月考数学试题
安徽省六安第一中学2023-2024学年高三上学期第二次月考数学试题湖南省部分校2022-2023学年高一下学期第一次阶段性诊断考试数学试题山西省2022-2023学年高一下学期3月联考数学试题山东省滨州高新高级中学2022-2023学年高一下学期4月月考数学试题(已下线)专题05 解三角形在几何与实际中的应用(2)-期中期末考点大串讲广东省佛山市南海区南海中学2022-2023学年高一下学期第二次阶段考数学试题青海省海东市2022-2023学年高一下学期4月联考数学试题四川省成都市新都香城中学2022-2023学年高一下学期4月测试数学试题四川省成都市城厢中学校2022-2023学年高一下学期期中考试数学试题(已下线)重难点专题02 解三角形的应用-2022-2023学年高一数学重难点题型分类必刷题(人教B版2019必修第四册)江西省吉安市双校联盟2022-2023学年高一下学期期中考试数学试题四川省凉山州宁南中学2023-2024学年高二上学期第一次月考数学试题辽宁省抚顺德才高级中学2023-2024学年高二上学期期初考试数学(北大班)试题(已下线)阶段性检测2.2(中)(范围:集合至复数)(已下线)考点20 三角函数的数学文化 --2024届高考数学考点总动员【练】四川省南充市仪陇县2023-2024学年高一下学期5月教学质量监测数学试题
4 . 已知两座灯塔A和B与海洋观察站C的距离都等于20km,灯塔A在观察站C的北偏东 ,灯塔B在观察站C的南偏东
,灯塔B在观察站C的南偏东 ,则灯塔A与灯塔B的距离为( )
,则灯塔A与灯塔B的距离为( )
 ,灯塔B在观察站C的南偏东
,灯塔B在观察站C的南偏东 ,则灯塔A与灯塔B的距离为( )
,则灯塔A与灯塔B的距离为( )| A.20km | B.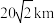 | C.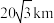 | D.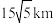 |
您最近一年使用:0次
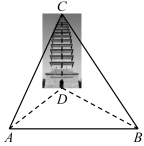
5 . 如图,有一古塔,在A点测得塔底位于北偏东 方向上的点D处,在A点测得塔顶C的仰角为
方向上的点D处,在A点测得塔顶C的仰角为 ,在A的正东方向且距D点30m的B点测得塔底位于西偏北
,在A的正东方向且距D点30m的B点测得塔底位于西偏北 方向上(A,B,D在同一水平面),则塔的高度CD约为(
方向上(A,B,D在同一水平面),则塔的高度CD约为( ,
,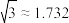 )( )
)( )
 方向上的点D处,在A点测得塔顶C的仰角为
方向上的点D处,在A点测得塔顶C的仰角为 ,在A的正东方向且距D点30m的B点测得塔底位于西偏北
,在A的正东方向且距D点30m的B点测得塔底位于西偏北 方向上(A,B,D在同一水平面),则塔的高度CD约为(
方向上(A,B,D在同一水平面),则塔的高度CD约为( ,
,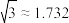 )( )
)( )
| A.17.32m | B.14.14m | C.10.98m | D.6.21m |
您最近一年使用:0次
2023-06-13更新
|
466次组卷
|
4卷引用:安徽省黄山市屯溪第一中学2024届高三第二次模拟考试数学试题(实验班用)
安徽省黄山市屯溪第一中学2024届高三第二次模拟考试数学试题(实验班用)江苏省连云港市灌南高级中学2022-2023学年高一下学期期中数学试题(已下线)第四章 三角函数与解三角形 第七节 解三角形应用举例(已下线)【讲】第六节 解三角形应用举例【北京一轮】
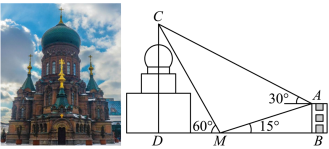
6 . 圣・索菲亚教堂(英语:SAINT SOPHIA CATHEDRAL)坐落于中国黑龙江省,是一座始建于1907年拜占庭风格的东正教教堂,距今已有114年的历史,为哈尔滨的标志性建筑.1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美.小明同学为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物 ,高为
,高为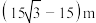 ,在它们之间的地面上的点
,在它们之间的地面上的点 (
(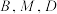 三点共线)处测得楼顶
三点共线)处测得楼顶 ,教堂顶
,教堂顶 的仰角分别是
的仰角分别是 和
和 ,在楼顶
,在楼顶 处测得塔顶
处测得塔顶 的仰角为
的仰角为 ,则小明估算索菲亚教堂的高度为
,则小明估算索菲亚教堂的高度为__________ 米.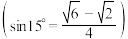
 ,高为
,高为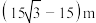 ,在它们之间的地面上的点
,在它们之间的地面上的点 (
(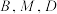 三点共线)处测得楼顶
三点共线)处测得楼顶 ,教堂顶
,教堂顶 的仰角分别是
的仰角分别是 和
和 ,在楼顶
,在楼顶 处测得塔顶
处测得塔顶 的仰角为
的仰角为 ,则小明估算索菲亚教堂的高度为
,则小明估算索菲亚教堂的高度为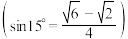
您最近一年使用:0次
2023-06-18更新
|
305次组卷
|
5卷引用:安徽省芜湖市2021-2022学年高一下学期期中考试数学试卷
7 . 信阳南湾湖以源远流长的历史遗产,浓郁丰厚的民俗风情而著称;以幽、朴、秀、奇的独特风格,山、水、林、岛的完美和谐而闻名,是融自然景观、人文景观、森林生态环境、森林保健功能于一体,是河南省著名的省级风景区.如图,为迎接第九届开渔节,某渔船在湖面上A处捕鱼时,天气预报几小时后会有恶劣天气,该渔船的东偏北 方向上有一个小岛C可躲避恶劣天气,在小岛C的正北方向有一航标灯D距离小岛25海里,渔船向小岛行驶50海里后到达B处,测得
方向上有一个小岛C可躲避恶劣天气,在小岛C的正北方向有一航标灯D距离小岛25海里,渔船向小岛行驶50海里后到达B处,测得 ,
, 海里.
海里.
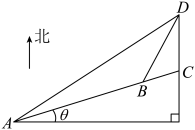
(1)求A处距离航标灯D的距离AD;
(2)求 的值;
的值;
(3)为保护南湾湖水源自然环境,请写出两条建议(言之有物即可).
 方向上有一个小岛C可躲避恶劣天气,在小岛C的正北方向有一航标灯D距离小岛25海里,渔船向小岛行驶50海里后到达B处,测得
方向上有一个小岛C可躲避恶劣天气,在小岛C的正北方向有一航标灯D距离小岛25海里,渔船向小岛行驶50海里后到达B处,测得 ,
, 海里.
海里.
(1)求A处距离航标灯D的距离AD;
(2)求
 的值;
的值;(3)为保护南湾湖水源自然环境,请写出两条建议(言之有物即可).
您最近一年使用:0次
2023-01-31更新
|
780次组卷
|
5卷引用:安徽省阜阳市江淮理工学校2022-2023学年高一下学期期中考试数学试卷
安徽省阜阳市江淮理工学校2022-2023学年高一下学期期中考试数学试卷河南省信阳市浉河区新时代学校2021-2022学年高二上学期第一次月考数学试题(已下线)专题07 平面几何中的向量方法 向量在物理中的应用-《重难点题型·高分突破》(人教A版2019必修第二册)(已下线)专题07 向量应用-《重难点题型·高分突破》(苏教版2019必修第二册)河南省新乡市原阳县实验高级中学2023-2024学年高一下学期3月月考数学试题
名校
解题方法
8 . 如图,一同学利用所学习的解三角形知识想测量河对岸的塔高 时,他选取了塔底B在同一水平面内的两个测量基点C与D.
时,他选取了塔底B在同一水平面内的两个测量基点C与D.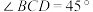 ,
, ,
, ,在点C处塔顶A的仰角为60°,则塔高为( )
,在点C处塔顶A的仰角为60°,则塔高为( )
 时,他选取了塔底B在同一水平面内的两个测量基点C与D.
时,他选取了塔底B在同一水平面内的两个测量基点C与D.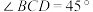 ,
, ,
, ,在点C处塔顶A的仰角为60°,则塔高为( )
,在点C处塔顶A的仰角为60°,则塔高为( )
A.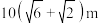 | B.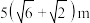 |
C.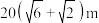 | D.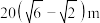 |
您最近一年使用:0次
2022-07-10更新
|
645次组卷
|
4卷引用:安徽省六安市独山中学2024-2025学年高二上学期开学考试数学试卷
安徽省六安市独山中学2024-2025学年高二上学期开学考试数学试卷湖北省新高考联考协作体2021-2022学年高一下学期期末数学试题青海省西宁市城西区青海湟川中学2022-2023学年高三上学期12月月考文科数学B试题(已下线)期末专题05 解三角形小题综合-【备战期末必刷真题】
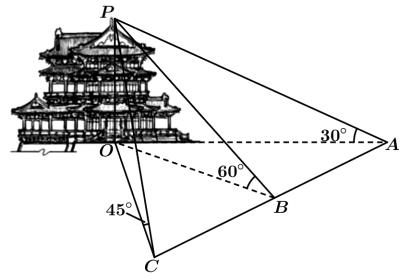
9 . 滕王阁,江南三大名楼之一,因初唐诗人王勃所作《滕王阁序》中的“落霞与孤鹜齐飞,秋水共长天一色”而名传千古,流芳后世.如图,在滕王阁旁地面上共线的三点 ,
, ,
, 处测得阁顶端点
处测得阁顶端点 的仰角分别为
的仰角分别为 ,
, ,
, .且
.且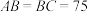 米,则滕王阁高度
米,则滕王阁高度
___________ 米.
 ,
, ,
, 处测得阁顶端点
处测得阁顶端点 的仰角分别为
的仰角分别为 ,
, ,
, .且
.且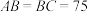 米,则滕王阁高度
米,则滕王阁高度
您最近一年使用:0次
2021-10-10更新
|
2227次组卷
|
18卷引用:安徽省十校联盟2021-2022学年高三上学期11月联考文科数学试题
安徽省十校联盟2021-2022学年高三上学期11月联考文科数学试题安徽省十校联盟2021-2022学年高三上学期11月联考理科数学试题安徽省马鞍山中加双语学校2022-2023学年高一下学期第二次月考数学试题河南省创新发展联盟2021-2022学年高二上学期9月联考数学试题(已下线)热点01 数学传统文化和实际民生为载体的创新题-2022年高考数学【热点·重点·难点】专练(新高考专用)(已下线)6.4.3 正、余弦定理的实际运用(精练)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第二册)广西贺州市2021-2022学年高二上学期全面质量检测数学(文)试题广西贺州市2021-2022学年高二上学期全面质量检测数学(理)试题北京市人大附中2021-2022学年高一下学期期中考试数学试题(已下线)第21节 解三角形宁夏吴忠市2023届高三下学期一轮联考数学(理)试题四川省眉山市眉山实验高级中学2021-2022学年高三上学期12月月考数学理科试题(已下线)专题06三角函数与解三角形(选择填空题)(已下线)模块一 情境2 以三角为背景江苏省泰州市田家炳实验中学2022-2023学年高一下学期期中数学试题山东省临沂市兰陵县第十中学2022-2023学年高一下学期5月月考数学试题甘肃省酒泉市2023-2024学年高一下学期7月期末考试数学试题【课后练】1.6.3 解三角形应用举例 课后作业-湘教版(2019)必修(第二册) 第1章 平面向量及其应用
名校
解题方法
10 . 下列说法中正确的是( )
A.若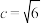 , , , , .则 .则 有两组解 有两组解 |
B.在 中,已知 中,已知 ,则 ,则 是等腰直角三角形 是等腰直角三角形 |
| C.两个不能到达的点之间无法求两点间的距离 |
D.在 中,若 中,若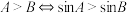 . . |
您最近一年使用:0次
2021-09-17更新
|
1663次组卷
|
5卷引用:安徽省滁州市定远县民族中学2022-2023学年高一下学期数学期末试卷
安徽省滁州市定远县民族中学2022-2023学年高一下学期数学期末试卷河北省张家口市第一中学2020-2021学年高一下学期期中数学试题(已下线)11.3 余弦定理、正弦定理的应用-2021-2022学年高一数学10分钟课前预习练(苏教版2019必修第二册)(已下线)第6章 平面向量及其应用(典型30题专练)-2021-2022学年高一数学考试满分全攻略(人教A版2019必修第二册)(已下线)山东省潍坊市2022-2023学年高二上学期开学检测数学试题



