名校
1 . 已知函数 .
.
(1)若 ,用定义证明
,用定义证明 在
在 上是增函数;
上是增函数;
(2)若 ,且
,且 在
在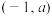 上的值域是
上的值域是 ,求
,求 的值.
的值.
 .
.(1)若
 ,用定义证明
,用定义证明 在
在 上是增函数;
上是增函数;(2)若
 ,且
,且 在
在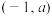 上的值域是
上的值域是 ,求
,求 的值.
的值.
您最近一年使用:0次
2019-10-29更新
|
211次组卷
|
2卷引用:福建省厦门市双十中学2019-2020学年高一上学期第一次月考数学试题
名校
解题方法
2 . 已知 定义域为
定义域为 ,对任意
,对任意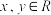 都有
都有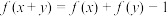 ,当
,当 时,
时,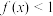 ,
,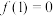 .
.
(1)求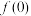 和
和 的值;
的值;
(2)试判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)解不等式: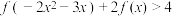 .
.
 定义域为
定义域为 ,对任意
,对任意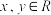 都有
都有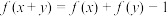 ,当
,当 时,
时,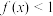 ,
,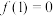 .
.(1)求
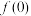 和
和 的值;
的值;(2)试判断
 在
在 上的单调性,并证明;
上的单调性,并证明;(3)解不等式:
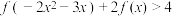 .
.
您最近一年使用:0次
2019-06-12更新
|
2470次组卷
|
2卷引用:【全国百强校】安徽省六安市第一中学2018-2019学年高二下学期第二次段考数学(文)试题
名校
解题方法
3 . 已知函数 的定义域为D,且
的定义域为D,且 同时满足以下条件:
同时满足以下条件:
① 在D上是单调递增或单调递减函数;
在D上是单调递增或单调递减函数;
②存在闭区间
 D(其中
D(其中 ),使得当
),使得当 时,
时, 的取值集合也是
的取值集合也是 .那么,我们称函数
.那么,我们称函数 (
( )是闭函数.
)是闭函数.
(1)判断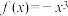 是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
(2)若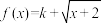 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.
(注:本题求解中涉及的函数单调性不用证明,直接指出是增函数还是减函数即可)
 的定义域为D,且
的定义域为D,且 同时满足以下条件:
同时满足以下条件:①
 在D上是单调递增或单调递减函数;
在D上是单调递增或单调递减函数;②存在闭区间

 D(其中
D(其中 ),使得当
),使得当 时,
时, 的取值集合也是
的取值集合也是 .那么,我们称函数
.那么,我们称函数 (
( )是闭函数.
)是闭函数.(1)判断
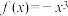 是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.(2)若
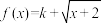 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.(注:本题求解中涉及的函数单调性不用证明,直接指出是增函数还是减函数即可)
您最近一年使用:0次
解题方法
4 . 已知二次函数f(x)=x2+bx+c有两个零点1和﹣1.
(1)求f(x)的解析式;
(2)设g(x)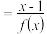 ,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
(3)由(2)函数g(x)在区间(﹣1,1)上,若实数t满足g(t﹣1)﹣g(﹣t)>0,求t的取值范围.
(1)求f(x)的解析式;
(2)设g(x)
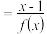 ,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;(3)由(2)函数g(x)在区间(﹣1,1)上,若实数t满足g(t﹣1)﹣g(﹣t)>0,求t的取值范围.
您最近一年使用:0次
2018-11-25更新
|
1022次组卷
|
5卷引用:【市级联考】福建省福州市2018-2019学年高一上学期期中联考数学试题
【市级联考】福建省福州市2018-2019学年高一上学期期中联考数学试题【校级联考】福建省福州市三校2018-2019学年高一上学期期中联考数学试题(已下线)第3章章末复习提升(课后作业,)-新教材2020-2021学年高一数学同步备课(人教B版必修第一册)(已下线)【新教材精创】第三章函数练习(2)-人教B版高中数学必修第—册(已下线)第三章 函数 本章小结
解题方法
5 . 已知函数 对任意的实数
对任意的实数 都有
都有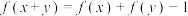 ,且当
,且当 时,
时, .
.
(1)求证:函数 在
在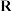 上是增函数;
上是增函数;
(2)若关于 的不等式
的不等式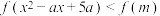 的解集为
的解集为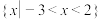 ,求
,求 的值.
的值.
 对任意的实数
对任意的实数 都有
都有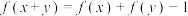 ,且当
,且当 时,
时, .
.(1)求证:函数
 在
在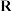 上是增函数;
上是增函数;(2)若关于
 的不等式
的不等式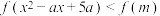 的解集为
的解集为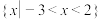 ,求
,求 的值.
的值.
您最近一年使用:0次
解题方法
6 . 已知定义在 上的函数
上的函数 对任意
对任意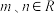 都有等式
都有等式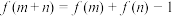 成立,且当
成立,且当 时,有
时,有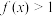 .
.
(1)求证:函数 在
在 上单调递增;
上单调递增;
(2)若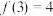 ,解关于
,解关于 的不等式
的不等式 .
.
 上的函数
上的函数 对任意
对任意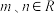 都有等式
都有等式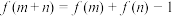 成立,且当
成立,且当 时,有
时,有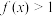 .
.(1)求证:函数
 在
在 上单调递增;
上单调递增;(2)若
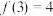 ,解关于
,解关于 的不等式
的不等式 .
.
您最近一年使用:0次
7 . 已知函数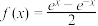 .
.
(1)判断 的奇偶性;
的奇偶性;
(2)用单调性的定义证明 为
为 上的增函数;
上的增函数;
(3)求满足不等式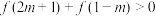 的实数
的实数 的取值范围.
的取值范围.
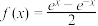 .
.(1)判断
 的奇偶性;
的奇偶性;(2)用单调性的定义证明
 为
为 上的增函数;
上的增函数;(3)求满足不等式
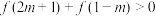 的实数
的实数 的取值范围.
的取值范围.
您最近一年使用:0次
2017-11-26更新
|
629次组卷
|
2卷引用:湖北省孝感市八校联考2017-2018学年高一上学期期中考试数学(文)试题
名校
解题方法
8 . 已知函数 的定义域为
的定义域为 ,当
,当 时,
时,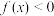 ,且对任意正实数
,且对任意正实数 ,满足
,满足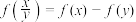 .
.
(1)求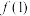 ;
;
(2)证明 在定义域上是减函数;
在定义域上是减函数;
(3)如果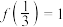 ,求满足不等式
,求满足不等式 的
的 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,当
,当 时,
时,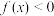 ,且对任意正实数
,且对任意正实数 ,满足
,满足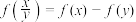 .
.(1)求
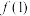 ;
;(2)证明
 在定义域上是减函数;
在定义域上是减函数;(3)如果
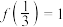 ,求满足不等式
,求满足不等式 的
的 的取值范围.
的取值范围.
您最近一年使用:0次
名校
解题方法
9 . 已知函数 的定义域为
的定义域为 ,对于任意的
,对于任意的 都有
都有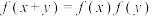 ,设
,设 时,
时,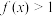 .
.
(1)求 ;
;
(2)证明:对于任意的 ,
, ;
;
(3)当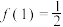 时,若不等式
时,若不等式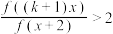 在
在 上恒定成立,求实数
上恒定成立,求实数 的取值范围.
的取值范围.
 的定义域为
的定义域为 ,对于任意的
,对于任意的 都有
都有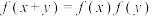 ,设
,设 时,
时,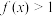 .
.(1)求
 ;
;(2)证明:对于任意的
 ,
, ;
;(3)当
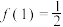 时,若不等式
时,若不等式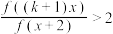 在
在 上恒定成立,求实数
上恒定成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2017-11-28更新
|
580次组卷
|
2卷引用:山西省太原市2017-2018学年高一上学期第一次测评(期中)数学试题
名校
解题方法
10 . 已知函数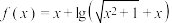 的定义域是
的定义域是 .
.
(1)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(2)若不等式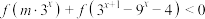 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
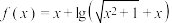 的定义域是
的定义域是 .
.(1)判断
 在
在 上的单调性,并证明;
上的单调性,并证明;(2)若不等式
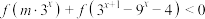 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2017-11-25更新
|
398次组卷
|
2卷引用:江西省赣州市寻乌中学2017-2018学年高一上学期期中考试数学试题



