10-11高一下·山东济宁·期末
名校
解题方法
1 . 已知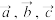 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(1)若 ,且
,且 ,求
,求 的坐标;
的坐标;
(2)若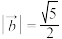 ,且
,且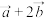 与
与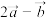 垂直,求
垂直,求 与
与 的夹角θ.
的夹角θ.
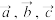 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.(1)若
 ,且
,且 ,求
,求 的坐标;
的坐标;(2)若
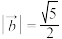 ,且
,且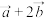 与
与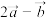 垂直,求
垂直,求 与
与 的夹角θ.
的夹角θ.
您最近一年使用:0次
2023-09-23更新
|
1463次组卷
|
101卷引用:2015-2016学年湖南省邵阳市邵东三中高一下期中数学试卷
2015-2016学年湖南省邵阳市邵东三中高一下期中数学试卷【全国校级联考】湖南省株洲市醴陵二中、醴陵四中2017-2018学年高一下学期期中联考数学试题【校级联考】湖南省醴陵二中、醴陵四中2018-2019学年高一下学期期中联考数学试题湖南省株洲市2019-2020学年高一上学期期中数学试题(已下线)山东省曲阜一中2010-2011学年高一下学期期末考试数学(已下线)2011-2012年辽宁省庄河六高高二上学期开学初考试联考理科数学(已下线)2011—2012学年云南省潞西市芒市中学高一下期中数学试卷(已下线)2012-2013学年安徽省泗县双语中学高一下学期期中考试数学试卷(已下线)2014届江苏省启东中学高三上学期期中模拟数学试卷(已下线)2013-2014学年浙江省宁波市八校高一上学期期末联考数学试卷(已下线)2013-2014学年四川省金阳中学高一3月月考数学试卷(已下线)2013-2014学年山东省济南一中高二下学期期中质量检测试卷(已下线)2013-2014学年广东省广州市越秀区高一下学期期末水平调研数学试卷(已下线)2013-2014学年甘肃兰州一中高一下学期期末考试数学试卷(已下线)2013-2014学年甘肃兰州一中高一下学期期末考试数学试卷2014-2015学年山东省临沭县高一下学期期中教学质量抽测数学试卷2014-2015学年广东省广州市四校高一下学期期中考试数学试卷2015-2016学年辽宁沈阳东北育才学校高二上学期第一次作业数学试卷2015-2016学年山东省寿光现代中学高一6月月考数学试卷2015-2016学年陕西省西安交大二附中南校区高一下期中数学试卷2017届重庆市第十一中学高三9月月考数学(文)试卷陕西省黄陵中学2017-2018学年高二(重点班)上学期开学考试数学试题广西南宁市马山县金伦中学2017-2018学年高二10月月考数学(文)试题(已下线)2017-2018学年上学期期末复习备考之精准复习模拟题高一数学必修三与必修四 (B卷)(第01期)【全国校级联考】河南省商丘市九校2017-2018学年高一下学期期末联考数学试题河南省开封市通许县实验中学2017-2018学年高一下学期期末考试数学试题河南省镇平县第一高级中学2017-2018学年高一下学期第三次月考数学试题(已下线)第4章 章末检测-2018-2019版数学创新设计课堂讲义同步系列(湘教版必修2)【全国百强校】吉林省长春外国语学校2018-2019学年高二下学期开学考试数学试题【市级联考】山西省运城市2018-2019学年高一下学期期中调研测试数学试题【全国百强校】河南省实验中学2018-2019学年高一下学期期中考试数学试题【全国百强校】河南省郑州第二中学2018-2019学年高一下期第二次月考(5月)数学试题吉林省五地六市联盟2018-2019学年高一下学期期末考试数学试题甘肃省金昌市永昌四中2018-2019学年高二下学期期末考试数学(理)试题江西省南昌市外国语学校、南昌一中2018-2019学年高一上学期期末联考数学试题上海市莘庄中学等四校2015-2016学年高二上学期11月联考数学试题山东省济宁市兖州区2018-2019学年高一下学期期中数学试题上海市宝山区宝山中学2017-2018学年高二上学期期中数学试题山西省运城市临猗县临晋中学2018-2019学年高一下学期期中数学试题人教A版(2019) 必修第二册 突围者 第六章 第三节课时3平面向量数量积的坐标表示上海市徐汇区2015-2016学年高二上学期期末数学试题吉林省长春市“BEST合作体”2018-2019学年高一下学期期末数学试题上海市青浦一中2016-2017学年高二上学期期中数学试题黑龙江省大庆市铁人中学2017-2018学年高一下学期开学考试数学试题专题04 平面向量数量积的坐标表示、平面向量的应用(核心素养练习)-【新教材精创】2019-2020高一数学新教材知识讲学(人教A版必修第二册)-《高中新教材知识讲学》陕西省西安市西北大学附中2018-2019学年高一下学期期中数学试题广东省佛山市第一中学2019-2020学年高一下学期第一次段考数学试题宁夏吴忠中学2019-2020学年高一4月网课学习第一次在线考试数学试题山东临沂市莒南第二中学2018-2019学年高一下学期素养水平检测试卷数学试题湖北省武汉市部分重点中学2019-2020学年高一下学期期中数学试题四川省遂宁市船山区第二中学校2019-2020学年高一下学期期中考试数学试题四川省自贡市田家炳中学2019-2020学年高一下学期期中考试数学试题陕西省延安市第一中学2019-2020学年高一下学期6月月考数学试题四川省绵阳市南山中学2018-2019学年高一下学期期中数学试题江西省宜春市宜丰县第二中学2019-2020学年高一下学期月考数学试题内蒙古通辽市2019-2020学年高一下学期期中考试数学(理)试卷西藏拉萨市第二高级中学2019-2020学年高一下学期期末测试数学试题云南省丽江市第一高级中学2019-2020学年高一下学期开学考试数学试题上海市奉城高级中学2017-2018学年高二上学期期末数学试题上海市奉城高级中学2019-2020学年高二上学期期末数学试题甘肃省白银市第十中学2018-2019学年高一上学期期中数学试题吉林省长春市第二实验中学2020-2021学年高一下学期4月月考数学试题青海省西宁市城西区青海湟川中学2020-2021学年高一上学期期末数学试题吉林省吉林市昌邑区吉林江城中学2019-2020学年高一下学期期末数学试题重庆市第三十七中学校2020-2021学年高一下学期期中数学试题河南省南阳市2020-2021学年高一下学期期末数学试题江西省进贤县第一中学2020-2021学年高一上学期期末考试数学试题四川省成都 蒲江县蒲江中学2020-2021学年高一下学期3月月考数学试题山西省朔州市应县第一中学2020-2021学年高一下学期3月月考数学(理)试题.江苏省南通市海安市南莫中学2020-2021学年高一下学期期中数学试题(已下线)上海期末真题精选50题(大题提升版)-2020-2021学年高一数学下册期中期末考试高分直通车(沪教版2020必修第二册)(已下线)9.3.2第2课时 向量数量积的坐标表示(备作业)-【上好课】2021-2022学年高一数学同步备课系列(苏教版2019必修第二册)甘肃省张掖市民乐县第一中学2021-2022学年高一下学期3月月考数学试题北京市房山中学2021-2022学年高一年级4月月考数学试题(已下线)6.3.5 平面向量数量积的坐标表示(课时作业)-2021-2022学年高一数学同步精品课件+课时作业(人教A版2019必修第二册)重庆市二0三中学2021-2022学年高一下学期3月月考数学试题海南省海口市第一中学2021-2022学年高一下学期期中考试数学试题(A)湖北省新高考联考协作体2021-2022学年高一下学期5月月考数学试题黑龙江省大庆市东风中学2021-2022学年高一下学期期中考试数学试题新疆乌鲁木齐市第一中学2021-2022学年高一下学期期末考试数学试题苏教版(2019) 必修第二册 过关斩将 第9章 本章达标检测吉林省白城市通榆县毓才高级中学2021-2022学年高一下学期第二次月考数学试题河南省安阳市开发区高级中学2020-2021学年高一上学期期末数学试题广西桂林市第十一中学2021-2022学年高一下学期期末阶段性质量数学试题江苏省盐城市响水县灌江高级中学2022-2023学年高一下学期期中数学试题5.2向量数量积的坐标表示5.3利用数量积计算长度与角度课后巩固提升习题2020-2021学年高一下学期数学北师大版(2019)必修第二册河北省承德市双滦区实验中学2022-2023学年高一下学期5月月考数学试题甘肃省临洮中学2022-2023学年高一下学期第二次月考数学试题(已下线)高一数学下学期期末模拟押题预测试卷(平面向量+解三角形+复数+立体几何+统计概率)-【题型分类归纳】山东省泰安市泰安一中新校区2022-2023学年高一下学期期中数学试题河南市柘城县德盛高级中学2022-2023学年高一下学期5月月考数学试题江苏省淮安市楚州中学、淮阴师范学院附属中学、新马高级中学2021-2022学年高一下学期期中联考数学试题云南省德宏州民族中学2015届高三上学期第二次月考数学(文)试题福建省宁德市福安市第一中学2023-2024学年高一下学期3月月考数学试题河北省石家庄一中东校区2023-2024学年高一下学期第一次月考数学试题山东省淄博中学2023-2024学年高一下学期4月月考数学试题广东省佛山市南海区桂华中学2023-2024学年高一下学期第一次阶段测试数学试卷湖北省十堰市房县第一中学2023-2024学年高一下学期第一次月考数学试题(已下线)上海市高一下学期期末真题必刷03-期末考点大串讲(沪教版2020必修二)河南省南阳市第一中学校2023-2024学年高一下学期第四次月考(6月)数学试题四川省成都市新津中学2021-2022学年高一下学期3月月考数学试题
名校
解题方法
2 . 已知 ,
, ,
,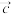 是同一平面内的三个不同向量,其中
是同一平面内的三个不同向量,其中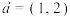 .
.
(1)若 ,且
,且 ,求
,求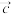 ;
;
(2)若 ,且
,且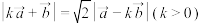 ,求
,求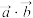 的最小值,并求出此时
的最小值,并求出此时 与
与 夹角的余弦值.
夹角的余弦值.
 ,
, ,
,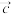 是同一平面内的三个不同向量,其中
是同一平面内的三个不同向量,其中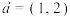 .
.(1)若
 ,且
,且 ,求
,求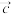 ;
;(2)若
 ,且
,且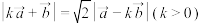 ,求
,求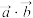 的最小值,并求出此时
的最小值,并求出此时 与
与 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2022-07-09更新
|
2572次组卷
|
13卷引用:湖南省邵阳市邵东市第一中学2022-2023学年高一下学期期中考试数学试题
湖南省邵阳市邵东市第一中学2022-2023学年高一下学期期中考试数学试题江苏省苏州市常熟市2021-2022学年高一下学期期中数学试题(已下线)6.2.4向量的数量积(分层作业)-【上好课】2022-2023学年高一数学同步备课系列(人教A版2019必修第二册)重难点:平面向量综合检测(提高卷)(已下线)高一下学期期中数学考试模拟卷03-2022-2023学年高一数学下学期期中期末考点大串讲(人教A版2019必修第二册)(已下线)模块二 专题1 《平面向量》单元检测篇 A基础卷 (苏教版)重庆市第十八中学2023-2024学年高一下学期3月月考数学试题云南省文山州广南县第十中学校2023-2024学年高一下学期3月月考数学试题广东省东莞市第一中学2023-2024学年高一下学期第一次段考数学试卷单元测试B卷——第六章 平面向量及其应用江西省南昌市第五高级中学2023-2024学年高一下学期期中考试数学试卷河北省石家庄二十三中2023-2024学年高二下学期期末数学试题四川省自贡市旭川中学2023-2024学年高一下学期第一次月考数学试题
名校
解题方法
3 . 已知平面向量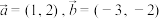 .
.
(1)若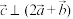 ,且
,且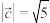 ,求
,求 的坐标;
的坐标;
(2)若 与
与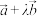 的夹角为锐角,求实数
的夹角为锐角,求实数 的取值范围.
的取值范围.
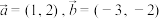 .
.(1)若
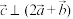 ,且
,且 ,求
,求 的坐标;
的坐标;(2)若
 与
与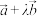 的夹角为锐角,求实数
的夹角为锐角,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2024-05-29更新
|
795次组卷
|
8卷引用:湖南省岳阳市岳阳楼区2022-2023学年高一下学期期末考试数学试题
4 . 已知 ,
, 为平面的单位向量,且其夹角为
为平面的单位向量,且其夹角为 ,若
,若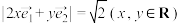 ,则
,则 的最大值为( )
的最大值为( )
 ,
, 为平面的单位向量,且其夹角为
为平面的单位向量,且其夹角为 ,若
,若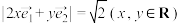 ,则
,则 的最大值为( )
的最大值为( )A. | B. | C. | D.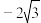 |
您最近一年使用:0次
2022-05-01更新
|
1801次组卷
|
5卷引用:湖南省长沙市长郡中学2022届高三高考前保温卷(一)数学试题
湖南省长沙市长郡中学2022届高三高考前保温卷(一)数学试题重庆市巴蜀中学校2022届高三下学期高考适应性月考(九)数学试题(已下线)专题04 基本不等式及其应用(已下线)6.2.4 向量的数量积 (精讲)(2)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)专题04 基本不等式及其应用-3
名校
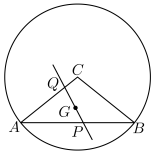
5 . 如图,圆心为C的定圆的半径为3,A,B为圆C上的两点.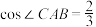 ,当k为何值时,
,当k为何值时,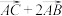 与
与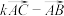 垂直?
垂直?
(2)若 的最小值为2,求
的最小值为2,求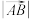 的值;
的值;
(3)若G为 的重心,直线l过点G交边
的重心,直线l过点G交边 于点P,交边
于点P,交边 于点Q,且
于点Q,且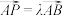 ,
,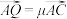 .证明:
.证明: 为定值.
为定值.
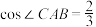 ,当k为何值时,
,当k为何值时,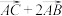 与
与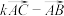 垂直?
垂直?(2)若
 的最小值为2,求
的最小值为2,求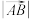 的值;
的值;(3)若G为
 的重心,直线l过点G交边
的重心,直线l过点G交边 于点P,交边
于点P,交边 于点Q,且
于点Q,且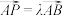 ,
,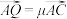 .证明:
.证明: 为定值.
为定值.
您最近一年使用:0次
2023-07-06更新
|
702次组卷
|
2卷引用:湖南省岳阳市岳阳县第一中学2022-2023学年高一下学期期末数学试题
名校
6 . 如图,在梯形 中,
中, ,
,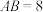 ,
,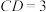 ,
,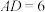 ,
, 在线段
在线段 上.
上.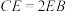 ,用向量
,用向量 ,
,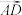 表示
表示 ,
,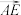 ;
;
(2)若AE与BD交于点F,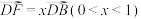 ,
,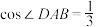 ,
, ,求
,求 的值.
的值.
 中,
中, ,
,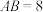 ,
,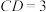 ,
,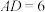 ,
, 在线段
在线段 上.
上.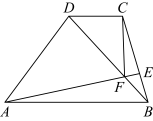
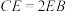 ,用向量
,用向量 ,
,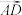 表示
表示 ,
,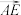 ;
;(2)若AE与BD交于点F,
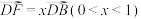 ,
,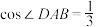 ,
, ,求
,求 的值.
的值.
您最近一年使用:0次
2024-05-19更新
|
469次组卷
|
4卷引用:湖南省岳阳县第一中学、汨罗市第一中学2023-2024学年高一下学期五月联考数学试题
名校
解题方法
7 . 已知在同一平面上的3个单位向量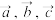 ,它们相互之间的夹角均为
,它们相互之间的夹角均为 ,且
,且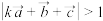 ,则实数k的取值范围是
,则实数k的取值范围是___________ .
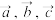 ,它们相互之间的夹角均为
,它们相互之间的夹角均为 ,且
,且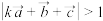 ,则实数k的取值范围是
,则实数k的取值范围是
您最近一年使用:0次
2022-05-14更新
|
806次组卷
|
4卷引用:湖南省长沙市长郡湘府中学2021-2022学年高一下学期期末模拟数学试题
湖南省长沙市长郡湘府中学2021-2022学年高一下学期期末模拟数学试题北京市第四中学2021-2022学年高一下期中数学试题(已下线)6.2.4 向量的数量积 (精讲)(2)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)专题9.3 向量的数量积运算-重难点突破及混淆易错规避(苏教版2019必修第二册)
解题方法
8 . 设非零向量 的夹角为
的夹角为 ,若
,若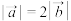 ,且不等式
,且不等式 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
 的夹角为
的夹角为 ,若
,若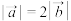 ,且不等式
,且不等式 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )A.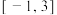 | B.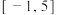 | C.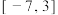 | D.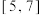 |
您最近一年使用:0次
2020-11-28更新
|
1751次组卷
|
13卷引用:【校级联考】湖南省岳阳一中、汨罗市一中2018-2019学年第二学期高一联考数学试题
【校级联考】湖南省岳阳一中、汨罗市一中2018-2019学年第二学期高一联考数学试题【全国校级联考】天一大联考2017-2018学年高一年级期末考试(安徽版)数学浙江省“七彩阳光”新高考研究联盟2020-2021学年高二上学期期中联考数学试题(已下线)【新东方】杭州新东方高中数学试卷382(已下线)【新东方】绍兴qw130(已下线)6.2.2 平面向量的数量积(精讲)-2020-2021学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)专题04 平面向量-【备战高考】2021年高三数学高考复习刷题宝典(单项选择专练)江苏省四校(上冈高级中学等)2020-2021学年高一下学期期中联考数学试题(已下线)6.2.4 向量的数量积1-2022-2023学年高一数学《考点·题型·技巧》精讲与精练高分突破系列(人教A版2019必修第二册) (已下线)专题6.3 向量的数量积-举一反三系列(已下线)专题04 向量的数量积(1)-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)专题04 向量的数量积(1)-《重难点题型·高分突破》(已下线)核心考点2 平面向量的数量积 专题讲解 (期末考试必考的10大核心考点)
名校
解题方法
9 . 已知向量 ,
, 的夹角为
的夹角为 ,且
,且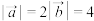 .
.
(1)求向量 在向量
在向量 上的投影向量;
上的投影向量;
(2)若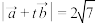 ,求
,求 的值.
的值.
 ,
, 的夹角为
的夹角为 ,且
,且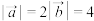 .
.(1)求向量
 在向量
在向量 上的投影向量;
上的投影向量;(2)若
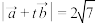 ,求
,求 的值.
的值.
您最近一年使用:0次
2024-05-02更新
|
285次组卷
|
4卷引用:湖南省部分学校2023-2024学年高一下学期期中联考数学试题
名校
解题方法
10 . 已知向量 满足
满足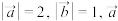 与
与 的夹角为
的夹角为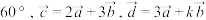 ,当实数
,当实数 为何值时,
为何值时,
(1) ;
;
(2)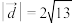 .
.
 满足
满足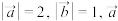 与
与 的夹角为
的夹角为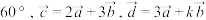 ,当实数
,当实数 为何值时,
为何值时,(1)
 ;
;(2)
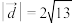 .
.
您最近一年使用:0次
2023-07-06更新
|
302次组卷
|
2卷引用:湖南省张家界市2022-2023学年高一下学期期末联考数学试题



