1 . (1)若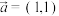 ,
,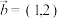 求
求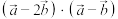 ;
;
(2)若 ,
, 为单位向量,
为单位向量, ,
, 的夹角为
的夹角为 ,求
,求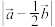 和函数
和函数 ,
, 的最小值;
的最小值;
(3)请在以下三个结论中任选一个用向量方法 证明.
①直径所对的圆周角是直角;②平行四边形的对角线的平方和等于其四边长的平方和;③三角形的三条中线交于一点.
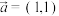 ,
,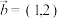 求
求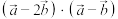 ;
;(2)若
 ,
, 为单位向量,
为单位向量, ,
, 的夹角为
的夹角为 ,求
,求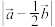 和函数
和函数 ,
, 的最小值;
的最小值;(3)请在以下三个结论中任选一个用
①直径所对的圆周角是直角;②平行四边形的对角线的平方和等于其四边长的平方和;③三角形的三条中线交于一点.
您最近半年使用:0次
名校
2 . “奔驰定理”因其几何表示酷似奔驰的标志得来,是平面向量中一个非常优美的结论.奔驰定理与三角形四心(重心、内心、外心、垂心)有着神秘的关联.它的具体内容是:已知 是
是 内一点,
内一点,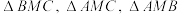 的面积分别为
的面积分别为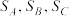 ,且
,且 .以下命题正确的有( )
.以下命题正确的有( )
 是
是 内一点,
内一点,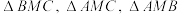 的面积分别为
的面积分别为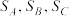 ,且
,且 .以下命题正确的有( )
.以下命题正确的有( )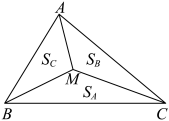
A.若 ,则 ,则 为 为 的重心 的重心 |
B.若 为 为 的内心,则 的内心,则 |
C.若 为 为 的外心,则 的外心,则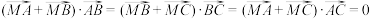 |
D.若 为 为 的垂心, 的垂心,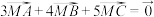 ,则 ,则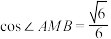 |
您最近半年使用:0次
2024·全国·模拟预测
3 . 在 中,命题
中,命题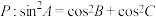 ,命题
,命题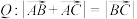 ,则P是Q的( )
,则P是Q的( )
 中,命题
中,命题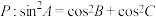 ,命题
,命题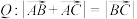 ,则P是Q的( )
,则P是Q的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
您最近半年使用:0次
名校
解题方法
4 . 已知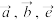 是平面向量,其中
是平面向量,其中 是单位向量,若非零向量
是单位向量,若非零向量 与
与 的夹角是
的夹角是 ,向量
,向量 满足
满足 ,则
,则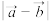 的最小值是
的最小值是__________ .
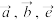 是平面向量,其中
是平面向量,其中 是单位向量,若非零向量
是单位向量,若非零向量 与
与 的夹角是
的夹角是 ,向量
,向量 满足
满足 ,则
,则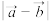 的最小值是
的最小值是
您最近半年使用:0次
解题方法
5 . 已知单位向量 的夹角为
的夹角为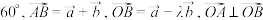 (
( 不重合),则
不重合),则 的值为( )
的值为( )
 的夹角为
的夹角为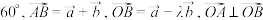 (
( 不重合),则
不重合),则 的值为( )
的值为( )A. | B.0 | C. | D. |
您最近半年使用:0次
6 . 已知向量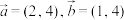 .
.
(1)求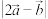 ;
;
(2)若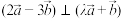 ,求
,求 的值.
的值.
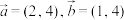 .
.(1)求
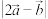 ;
;(2)若
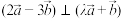 ,求
,求 的值.
的值.
您最近半年使用:0次
7 .  中,
中, 、
、 、
、 分别是内角
分别是内角 、
、 、
、 的对边,若
的对边,若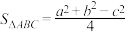 且
且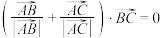 ,则
,则 形状是( )
形状是( )
 中,
中, 、
、 、
、 分别是内角
分别是内角 、
、 、
、 的对边,若
的对边,若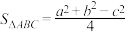 且
且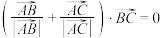 ,则
,则 形状是( )
形状是( )A.有一个角是 的等腰三角形 的等腰三角形 | B.顶角是 的等腰三角形 的等腰三角形 |
| C.等腰直角三角形 | D.不能确定三角形的形状 |
您最近半年使用:0次
8 . 已知 ,
, ,
, 、
、 的夹角
的夹角 ,若
,若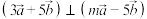 ,则
,则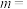
___________ .
 ,
, ,
, 、
、 的夹角
的夹角 ,若
,若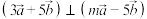 ,则
,则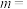
您最近半年使用:0次
解题方法
9 . 已知向量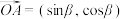 ,将向量
,将向量 可绕坐标原点O逆时针旋转
可绕坐标原点O逆时针旋转 角得到向量
角得到向量 (
(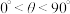 ),则下列说法正确的是( )
),则下列说法正确的是( )
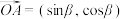 ,将向量
,将向量 可绕坐标原点O逆时针旋转
可绕坐标原点O逆时针旋转 角得到向量
角得到向量 (
(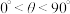 ),则下列说法正确的是( )
),则下列说法正确的是( )A.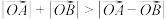 | B.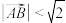 |
C. | D. |
您最近半年使用:0次
10 . 已知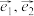 是夹角为
是夹角为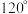 的两个单位向量,
的两个单位向量, 与
与 的夹角为
的夹角为 .
.
(1)求 ;
;
(2)若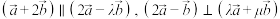 ,求
,求 .
.
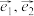 是夹角为
是夹角为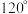 的两个单位向量,
的两个单位向量, 与
与 的夹角为
的夹角为 .
.(1)求
 ;
;(2)若
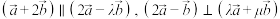 ,求
,求 .
.
您最近半年使用:0次



