1 . 解不等式组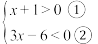 .第一步:解不等式①,得
.第一步:解不等式①,得____________ ;第二步:解不等式②,得__________ ;
第三步:在数轴上分别把不等式①②的解的范围表示出来,
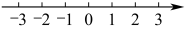
第四步:从两个范围中找出公共部分,得不等式组的解为_____________ .
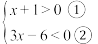 .第一步:解不等式①,得
.第一步:解不等式①,得第三步:在数轴上分别把不等式①②的解的范围表示出来,
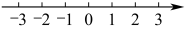
第四步:从两个范围中找出公共部分,得不等式组的解为
您最近一年使用:0次
解题方法
2 . 行列式是线性代数的一个重要研究对象,本质上,行列式描述的是n维空间中,一个线性变换所形成的平行多面体的体积,它被广泛应用于解线性方程组,矩阵运算,计算微积分等.在数学中,我们把形如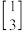 ,
,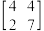 ,
,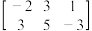 这样的矩形数字(或字母)阵列称作矩阵.我们将二阶矩阵
这样的矩形数字(或字母)阵列称作矩阵.我们将二阶矩阵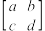 两边的“[ ]”改为“
两边的“[ ]”改为“ ”,得到二阶行列式
”,得到二阶行列式 ,它的运算结果是一个数值(或多项式),记为
,它的运算结果是一个数值(或多项式),记为 .
.
(1)求二阶行列式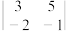 的值;
的值;
(2)求不等式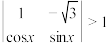 的解集;
的解集;
(3)若存在 ,使得
,使得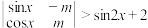 ,求m的取值范围.
,求m的取值范围.
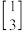 ,
,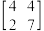 ,
,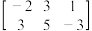 这样的矩形数字(或字母)阵列称作矩阵.我们将二阶矩阵
这样的矩形数字(或字母)阵列称作矩阵.我们将二阶矩阵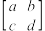 两边的“[ ]”改为“
两边的“[ ]”改为“ ”,得到二阶行列式
”,得到二阶行列式 ,它的运算结果是一个数值(或多项式),记为
,它的运算结果是一个数值(或多项式),记为 .
.(1)求二阶行列式
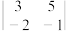 的值;
的值;(2)求不等式
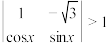 的解集;
的解集;(3)若存在
 ,使得
,使得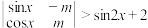 ,求m的取值范围.
,求m的取值范围.
您最近一年使用:0次
2024-07-04更新
|
277次组卷
|
3卷引用:贵州省遵义市2023-2024学年高一下学期5月期中数学试题
名校
解题方法
3 . 设函数 .
.
(1)若 ,解不等式
,解不等式 ;
;
(2)若 ,解关于x的不等式
,解关于x的不等式
 .
.(1)若
 ,解不等式
,解不等式 ;
;(2)若
 ,解关于x的不等式
,解关于x的不等式
您最近一年使用:0次
2022-05-02更新
|
1459次组卷
|
5卷引用:贵州省遵义航天高级中学2021-2022学年高一上学期第三次月考数学试题
贵州省遵义航天高级中学2021-2022学年高一上学期第三次月考数学试题辽宁省锦州市锦州中学2022-2023学年高一上学期第一次月考(10月)数学试题内蒙古通辽第五中学2022-2023学年高一上学期期中数学试题(已下线)第10讲 二次函数与一元二次方程、不等式6种题型(1)-【同步题型讲义】(人教A版2019必修第一册)(已下线)专题04 含参数的一元二次分类讨论策略-2023届高考数学一轮复习精讲精练(新高考专用)
名校
4 . 已知函数 ,
,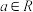 .
.
(1)若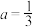 ,解不等式
,解不等式 ;
;
(2)解关于x的不等式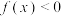 .
.
 ,
,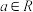 .
.(1)若
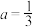 ,解不等式
,解不等式 ;
;(2)解关于x的不等式
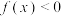 .
.
您最近一年使用:0次
2021-10-30更新
|
878次组卷
|
3卷引用:贵州省黔西南州金成实验学校2021-2022学年高一上学期期中质量检测数学试题
名校
解题方法
5 . (1)计算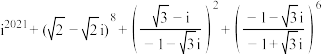 ;
;
(2)已知关于 的方程
的方程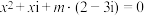 有实数解,求纯虚数
有实数解,求纯虚数 .
.
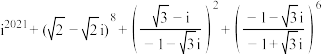 ;
;(2)已知关于
 的方程
的方程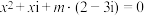 有实数解,求纯虚数
有实数解,求纯虚数 .
.
您最近一年使用:0次
2024-04-14更新
|
466次组卷
|
2卷引用:贵州省贵阳市六校(六中、二中、八中、十二中、省实、贵阳高中)2023-2024学年高一下学期第一次联考数学试题
解题方法
6 . 已知 为奇函数.
为奇函数.
(1)求a的值;
(2)解方程 ;
;
(3)解不等式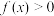 .
.
 为奇函数.
为奇函数.(1)求a的值;
(2)解方程
 ;
;(3)解不等式
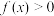 .
.
您最近一年使用:0次
7 . 求下列方程或不等式的解集.
(1)解方程 ;
;
(2)解不等式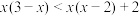 .
.
(1)解方程
 ;
;(2)解不等式
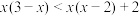 .
.
您最近一年使用:0次
2021-12-09更新
|
787次组卷
|
2卷引用:贵州省仁怀市第四中学2023-2024学年高一上学期10月月考数学试题
解题方法
8 . (1)对于 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)解关于 的不等式
的不等式 .
.
 恒成立,求
恒成立,求 的取值范围;
的取值范围;(2)解关于
 的不等式
的不等式 .
.
您最近一年使用:0次
名校
解题方法
9 . 材料1.类比是获取数学知识的重要思想之一,很多优美的数学结论就是利用类比思想获得的.例如:若 ,
, ,则
,则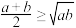 ,当且仅当
,当且仅当 时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式:
时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式: ,
, ,
, ,则
,则 ,当且仅当
,当且仅当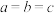 时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.
时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.
题:将边长为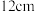 的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.
的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.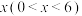 ,则纸盒容积
,则纸盒容积

当且仅当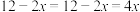 ,即
,即 时取等号.所以纸金的容积取得最大值
时取等号.所以纸金的容积取得最大值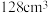 .在求
.在求 的最大值中,用均值不等式求最值时,遵循“一正二定三相等”的规则.你也可以将
的最大值中,用均值不等式求最值时,遵循“一正二定三相等”的规则.你也可以将 变形为
变形为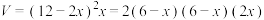 求解.
求解.
你还可以设纸盒的底面边长为 ,高为
,高为 ,则
,则 ,则纸盒容积
,则纸盒容积
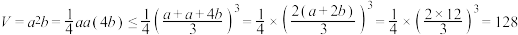 .
.
当且仅当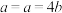 ,即
,即 ,
, 时取等号,所以纸盒的容积取得最大值
时取等号,所以纸盒的容积取得最大值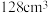 .
.
材料2.《数学必修二》第八章8.3节习题8.3设置了如下第4题:
如图1,圆锥的底面直径和高均为 ,过
,过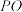 的中点
的中点 作平行于底面的截面,以该截面为底的面挖去一个圆柱,求剩下几何体的表面积和体积.我们称圆柱为圆锥的内接圆柱.
作平行于底面的截面,以该截面为底的面挖去一个圆柱,求剩下几何体的表面积和体积.我们称圆柱为圆锥的内接圆柱.
根据材料1与材料2完成下列问题.
如图2,底面直径和高均为 的圆锥有一个底面半径为
的圆锥有一个底面半径为 ,高为
,高为 的内接圆柱.
的内接圆柱. 与
与 的关系式;
的关系式;
(2)求圆柱侧面积的最大值;
(3)求圆柱体积的最大值.
 ,
, ,则
,则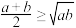 ,当且仅当
,当且仅当 时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式:
时,取等号,我们称为二元均值不等式.类比二元均值不等式得到三元均值不等式: ,
, ,
, ,则
,则 ,当且仅当
,当且仅当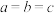 时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.
时,取等号.我们经常用它们求相关代数式或几何问题的最值,某同学做下面几何问题就是用三元均值不等式圆满完成解答的.题:将边长为
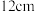 的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.
的正方形硬纸片(如图1)的四个角裁去四个相同的小正方形后,折成如图2的无盖长方体小纸盒,求纸盒容积的最大值.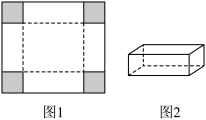
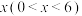 ,则纸盒容积
,则纸盒容积
当且仅当
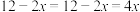 ,即
,即 时取等号.所以纸金的容积取得最大值
时取等号.所以纸金的容积取得最大值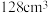 .在求
.在求 的最大值中,用均值不等式求最值时,遵循“一正二定三相等”的规则.你也可以将
的最大值中,用均值不等式求最值时,遵循“一正二定三相等”的规则.你也可以将 变形为
变形为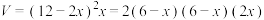 求解.
求解.你还可以设纸盒的底面边长为
 ,高为
,高为 ,则
,则 ,则纸盒容积
,则纸盒容积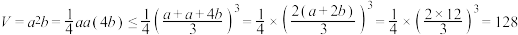 .
.当且仅当
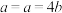 ,即
,即 ,
, 时取等号,所以纸盒的容积取得最大值
时取等号,所以纸盒的容积取得最大值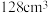 .
.材料2.《数学必修二》第八章8.3节习题8.3设置了如下第4题:
如图1,圆锥的底面直径和高均为
 ,过
,过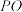 的中点
的中点 作平行于底面的截面,以该截面为底的面挖去一个圆柱,求剩下几何体的表面积和体积.我们称圆柱为圆锥的内接圆柱.
作平行于底面的截面,以该截面为底的面挖去一个圆柱,求剩下几何体的表面积和体积.我们称圆柱为圆锥的内接圆柱.根据材料1与材料2完成下列问题.
如图2,底面直径和高均为
 的圆锥有一个底面半径为
的圆锥有一个底面半径为 ,高为
,高为 的内接圆柱.
的内接圆柱.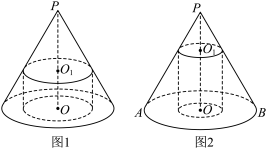
 与
与 的关系式;
的关系式;(2)求圆柱侧面积的最大值;
(3)求圆柱体积的最大值.
您最近一年使用:0次
解题方法
10 . (1)已知 满足
满足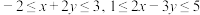 ,求x的取值范围;
,求x的取值范围;
(2)解关于x的不等式: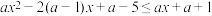 .
.
 满足
满足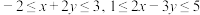 ,求x的取值范围;
,求x的取值范围;(2)解关于x的不等式:
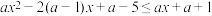 .
.
您最近一年使用:0次
2022-11-13更新
|
142次组卷
|
2卷引用:贵州省遵义市凤冈县2022-2023学年高一上学期期中联考数学试题



