名校
1 . 魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海岛的高.如图1,点 ,
, ,
, 在水平线
在水平线 上,
上, 和
和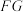 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,
是两个垂直于水平面且等高的测量标杆的高度,称为“表高”, 称为“表距”,
称为“表距”, 和
和 都称为“表目距”,
都称为“表目距”, 与
与 的差称为“表目距的差”,则海岛的高
的差称为“表目距的差”,则海岛的高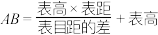 ,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线
,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线 上,同时在水平线
上,同时在水平线 上放一个小镜子(视为点
上放一个小镜子(视为点 ),他在距离镜子
),他在距离镜子 米点
米点 时,通过镜子看到了山顶,然后沿水平线
时,通过镜子看到了山顶,然后沿水平线 向靠近山的方向走了
向靠近山的方向走了 米,到达
米,到达 点,再将镜子放在距离自己
点,再将镜子放在距离自己 米的前方点
米的前方点 处,此时又看到了山顶,若此人的眼睛到水平线
处,此时又看到了山顶,若此人的眼睛到水平线 的距离为
的距离为 米,则此山的高度约为( )米
米,则此山的高度约为( )米

 ,
, ,
, 在水平线
在水平线 上,
上, 和
和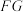 是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,
是两个垂直于水平面且等高的测量标杆的高度,称为“表高”, 称为“表距”,
称为“表距”, 和
和 都称为“表目距”,
都称为“表目距”, 与
与 的差称为“表目距的差”,则海岛的高
的差称为“表目距的差”,则海岛的高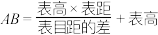 ,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线
,某同学受此法的启发设计了另一种测量此山高度的方案(如图2);他站在水平线 上,同时在水平线
上,同时在水平线 上放一个小镜子(视为点
上放一个小镜子(视为点 ),他在距离镜子
),他在距离镜子 米点
米点 时,通过镜子看到了山顶,然后沿水平线
时,通过镜子看到了山顶,然后沿水平线 向靠近山的方向走了
向靠近山的方向走了 米,到达
米,到达 点,再将镜子放在距离自己
点,再将镜子放在距离自己 米的前方点
米的前方点 处,此时又看到了山顶,若此人的眼睛到水平线
处,此时又看到了山顶,若此人的眼睛到水平线 的距离为
的距离为 米,则此山的高度约为( )米
米,则此山的高度约为( )米
A.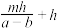 | B.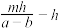 | C.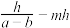 | D. |
您最近一年使用:0次
2 . 文化广场原名地质宫广场,是长春市著名的城市广场,历史上地质宫广场曾被规划为伪满洲国的国都广场.文化广场以新民主大街道路中心线至地质宫广场主楼中央为南北主轴,广场的中央是太阳鸟雕塑塔,在地质宫(现为吉林大学地质博物馆)主楼辉映下显得十分壮观.现某兴趣小组准备在文化广场上对中央太阳鸟雕塑塔的高度进行测量,并绘制出测量方案示意图,A为太阳鸟雕塑最顶端,B为太阳鸟雕塑塔的基座(即B在A的正下方),在广场内(与B在同一水平面内)选取C、D两点.测得CD的长为m.兴趣小组成员利用测角仪可测得的角有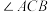 、
、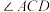 、
、 、
、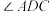 、
、 ,则根据下列各组中的测量数据,不能计算出太阳鸟雕塑塔高度AB的是( )
,则根据下列各组中的测量数据,不能计算出太阳鸟雕塑塔高度AB的是( )

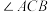 、
、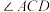 、
、 、
、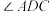 、
、 ,则根据下列各组中的测量数据,不能计算出太阳鸟雕塑塔高度AB的是( )
,则根据下列各组中的测量数据,不能计算出太阳鸟雕塑塔高度AB的是( )
A.m、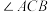 、 、 、 、 | B.m、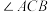 、 、 、 、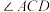 |
C.m、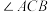 、 、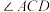 、 、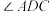 | D.m、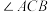 、 、 、 、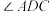 |
您最近一年使用:0次
2022-11-19更新
|
869次组卷
|
7卷引用:数学(江苏A卷)
(已下线)数学(江苏A卷)江苏省扬州市宝应县2022-2023学年高三上学期期末模拟数学试题吉林省长春市2023届高三上学期质量监测(一)数学试题(已下线)技巧03 数学文化与数学阅读解题策略(精讲精练)-1湖南省岳阳县第一中学2022-2023学年高三下学期第一次月考数学试题(已下线)6.4.3第3课时余弦定理、正弦定理应用举例(精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)第六章 突破立体几何创新问题 专题二 融合科技、社会热点 微点3 融合科技、社会热点等现代文化的立体几何和问题综合训练【培优版】
3 . 10世纪阿拉伯天文学家阿尔库希设计出一种方案,通过两个观察者异地同时观测同一颗小天体来测定小天体的高度.如图,有两个观察者在地球上A,B两地同时观测到一颗卫星S,仰角分别为∠SAM和∠SBM(MA,MB表示当地的水平线,即为地球表面的切线),设地球半径为R, 的长度为
的长度为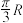 ,∠SAM=30°,∠SBM=45°,则卫星S到地面的高度为
,∠SAM=30°,∠SBM=45°,则卫星S到地面的高度为______ .
 的长度为
的长度为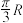 ,∠SAM=30°,∠SBM=45°,则卫星S到地面的高度为
,∠SAM=30°,∠SBM=45°,则卫星S到地面的高度为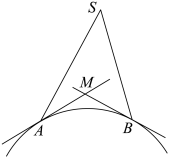
您最近一年使用:0次
2022-11-09更新
|
484次组卷
|
5卷引用:江苏省连云港市2022-2023学年高三上学期期中数学试题
4 . 瀑布是庐山的一大奇观,唐代诗人李白曾在《望庐山瀑布中》写道:日照香炉生紫烟,遥看瀑布挂前川,飞流直下三千尺,疑是银河落九天.为了测量某个瀑布的实际高度,某同学设计了如下测量方案:沿一段水平山道步行至与瀑布底端在同一水平面时,在此位置测得瀑布顶端的仰角正切值为 ,沿山道继续走20
,沿山道继续走20 ,测得瀑布顶端的仰角为
,测得瀑布顶端的仰角为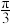 .已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为
.已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为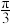 .根据这位同学的测量数据,可知该瀑布的高度为
.根据这位同学的测量数据,可知该瀑布的高度为___________  ;若第二次测量后,继续行进的山道有坡度,坡角大小为
;若第二次测量后,继续行进的山道有坡度,坡角大小为 ,且两段山道位于同一平面内,若继续沿山道行进
,且两段山道位于同一平面内,若继续沿山道行进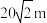 ,则该同学望向瀑布顶端与底端的视角正切值为
,则该同学望向瀑布顶端与底端的视角正切值为___________ .(此人身高忽略不计)
 ,沿山道继续走20
,沿山道继续走20 ,测得瀑布顶端的仰角为
,测得瀑布顶端的仰角为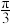 .已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为
.已知该同学沿山道行进的方向与他第一次望向瀑布底端的方向所成角为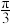 .根据这位同学的测量数据,可知该瀑布的高度为
.根据这位同学的测量数据,可知该瀑布的高度为 ;若第二次测量后,继续行进的山道有坡度,坡角大小为
;若第二次测量后,继续行进的山道有坡度,坡角大小为 ,且两段山道位于同一平面内,若继续沿山道行进
,且两段山道位于同一平面内,若继续沿山道行进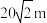 ,则该同学望向瀑布顶端与底端的视角正切值为
,则该同学望向瀑布顶端与底端的视角正切值为
您最近一年使用:0次
2022-08-13更新
|
1341次组卷
|
8卷引用:11.3 余弦定理、正弦定理的应用-【帮课堂】(苏教版2019必修第二册)
(已下线)11.3 余弦定理、正弦定理的应用-【帮课堂】(苏教版2019必修第二册)河北省衡水中学2022届高三下学期素养提升五数学试题(已下线)专题02 解三角形实际问题(已下线)模块四 三角函数、平面向量与解三角形-3(已下线)6.4.3第3课时余弦定理、正弦定理应用举例(精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)专题4 三角函数与解三角形2022年新高考原创密卷数学试题(六)(已下线)考点16 解三角形实际应用问题 --2024届高考数学考点总动员【练】
5 . 现有《诗经》、《尚书》、《礼记》、《周易》、《春秋》各一本,分给甲、乙、丙、丁、戊5名同学,每人一本,若甲乙都没有拿到《诗经》,且乙也没拿到《春秋》,则所有可能的分配方案有( )
| A.18种 | B.24种 | C.36种 | D.54种 |
您最近一年使用:0次
6 . 如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”.现提供4种颜色给“弦图”的5个区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
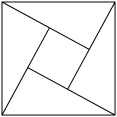
| A.48种 | B.72种 | C.96种 | D.144种 |
您最近一年使用:0次
2020-05-26更新
|
760次组卷
|
8卷引用:江苏省扬州市邗江中学2019-2020学年高二下学期期中数学试题
7 . 如图,《宋人扑枣图轴》是作于宋朝的中国古画,现收藏于中国台北故宫博物馆.有甲、乙、丙三人想根据该图编排一个舞蹈,首先由他们来选取该图中小孩扑枣的爬、扶、捡、顶、摇中的五个动作,每人至少模仿一个动作,且爬、扶、捡、顶、摇都要被依序模仿到,则选择的方案共有( )


| A.60种 | B.90种 | C.100种 | D.150种 |
您最近一年使用:0次
名校
8 . 概率论起源于博弈游戏.17世纪,曾有一个“赌金分配“的问题:博弈水平相当的甲、乙两人进行博弈游戏,每局比赛都能分出胜负,没有平局.双方约定,各出赌金48枚金币,先赢3局者可获得全部赌金;但比赛中途因故终止了,此时甲赢了2局,乙赢了1局.问这96枚金币的赌金该如何分配?数学家费马和帕斯卡都用了现在称之为“概率“的知识,合理地给出了赌金分配方案.该分配方案是
| A.甲48枚,乙48枚 | B.甲64枚,乙32枚 |
| C.甲72枚,乙24枚 | D.甲80枚,乙16枚 |
您最近一年使用:0次
2020-05-07更新
|
2436次组卷
|
12卷引用:江苏省南通市通州区石港中学2022-2023学年高二下学期第三次阶段检测数学试题
江苏省南通市通州区石港中学2022-2023学年高二下学期第三次阶段检测数学试题江苏省常州高级中学2023-2024学年高二上学期暑期作业反馈检测数学试题2020届福建省福州市高三质量检测理科数学试题湖南省长沙市长郡中学2021届高三下学期月考(六)数学试题湖北省武汉市洪山高级中学2021-2022学年高二上学期第一次月考数学试题(已下线)期末测试卷-2021-2022学年高一数学课后培优练(人教A版2019必修第二册)(已下线)专题10.1 概率 章末检测1(易)-【满分计划】2021-2022学年高一数学阶段性复习测试卷(人教A版2019必修第二册)江西省赣州市信丰中学2021-2022学年高二下学期3月月考数学(理)试题浙江省北斗联盟2022-2023学年高二下学期期中联考数学试题(已下线)第10章 概率 章末测试(提升)-一隅三反系列(人教A版2019必修第二册)安徽省定远中学2022-2023学年高二下学期5月月考数学试卷(已下线)专题02 事件的相互独立性(题型专练)-《知识解读·题型专练》(人教A版2019必修第二册)
2020高三·浙江·专题练习
名校
9 . 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )
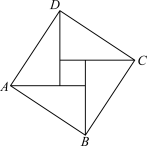

| A.180 | B.192 | C.420 | D.480 |
您最近一年使用:0次
2020-01-04更新
|
2097次组卷
|
16卷引用:江苏省常州市横林高级中学2021—2022学年高二下学期5月阶段调研数学试题
江苏省常州市横林高级中学2021—2022学年高二下学期5月阶段调研数学试题(已下线)高二数学下学期第二次月考模拟试卷(选择性必修第二册,含数列和导数)-【题型分类归纳】2022-2023学年高二数学同步讲与练(苏教版2019选择性必修第二册)(已下线)【新东方】杭州高三数学试卷262浙江省“9+1”高中联盟2019-2020学年高三上学期期中数学试题黑龙江大庆实验中学2019-2020学年下学期实验三部期中考试高二数学理科试题黑龙江大庆实验中学2019-2020学年高二下学期线上期中考试数学(理)试题广东省珠海市2019-2020学年高二(下)期末数学试题重庆市渝东八校2019-2020学年高二下学期期中数学试题人教B版(2019) 选择性必修第二册 过关斩将 第三章 排列、组合与二项式定理 本章达标检测(已下线)【新东方】双师232高二下(已下线)【新东方】 双师278高二下(已下线)第六章 计数原理(基础训练)A卷-2021-2022学年高二数学课后培优练(人教A版2019选择性必修第三册)福建省永春第一中学2021-2022学年高二4月线上考试数学试题北京市十一学校2021-2022学年高二下学期第3学段教与学诊断(期中)数学试题黑龙江省哈尔滨市尚志市尚志中学2021-2022学年高二下学期6月月考数学试题河南省南阳市第一中学校2022-2023学年高二上学期12月月考数学试题
名校
10 . 如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有种
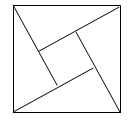
| A.120 | B.260 | C.340 | D.420 |
您最近一年使用:0次
2018-04-12更新
|
3555次组卷
|
20卷引用:江苏省苏州市张家港市沙洲中学2023-2024学年高二下学期3月阶段性测试数学试题
江苏省苏州市张家港市沙洲中学2023-2024学年高二下学期3月阶段性测试数学试题重庆市第一中学2017-2018学年高二下学期第一次月考数学(理)试题河南省郑州一中2017-2018学年高二下学期期末复习理科数学试题【校级联考】河南省唐河县友兰实验高中2018-2019学年高二下学期第二次月考(理)数学试题天津市第一中学2020-2021学年高二下学期期中数学试题吉林省延边第二中学2020-2021学年高二下学期期中考试数学(理)试题人教A版(2019) 选修第三册 必杀技 6.1分类加法计数原理与分步乘法计数原理北师大版(2019) 选修第一册 必杀技 第五章 §1基本计数原理北师大版(2019) 选修第一册 突围者 第五章 全章综合检测人教A版(2019) 选修第三册 突围者 第六章 素养拓展(已下线)第九课时 课后 第六章 章末复习课(已下线)第49讲 计数原理 排列与组合(练) — 2022年高考数学一轮复习讲练测(课标全国版)(已下线)第03讲 分类加法计数原理与分布乘法计数原理-【寒假自学课】2022年高二数学寒假精品课(人教A版2019选择性必修第三册)(已下线)复习题五1天津市南开大学附属中学2021-2022学年高二下学期期中数学试题(已下线)第6章 计数原理(典型30题专练)2021-2022学年高二数学下学期考试满分全攻略(人教A版2019选修第二册+第三册)陕西省渭南市临渭区2021-2022学年高二下学期期末理科数学试题广东省江门市新会东方红中学2021-2022学年高二下学期期中数学试题第五章 计数原理 核心素养定心卷-2021-2022学年高二上学期数学北师大版(2019)选择性必修第一册北师大版(2019) 选修第一册 数学奇书 学业评价(三十二) 分类加法计数原理 分步乘法计数原理 基本计数原理的简单应用



