1 . 某中学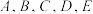 五名高一学生选择甲、乙、丙、丁四个社团进行实践活动,每名学生只能选一个社团,则下列结论中正确的是( )
五名高一学生选择甲、乙、丙、丁四个社团进行实践活动,每名学生只能选一个社团,则下列结论中正确的是( )
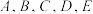 五名高一学生选择甲、乙、丙、丁四个社团进行实践活动,每名学生只能选一个社团,则下列结论中正确的是( )
五名高一学生选择甲、乙、丙、丁四个社团进行实践活动,每名学生只能选一个社团,则下列结论中正确的是( )A.所有不同的分派方案共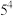 种 种 |
| B.若甲社团没人选,乙、丙、丁每个社团至少有一个学生选,则所有不同的分派方案共300种 |
C.若每个社团至少派1名志愿者,且志愿者 必须到甲社团,则所有不同分派方案共60种 必须到甲社团,则所有不同分派方案共60种 |
D.若每个社团至少有1个学生选,且学生 不安排到同一社团,则所有不同分派方案共216种 不安排到同一社团,则所有不同分派方案共216种 |
您最近一年使用:0次
2 . 某职业技术学校组织6名学生到3家工厂实习,每家工厂至少去1人,至多去3人,且每名学生只能去1家工厂,则不同的分配方法共有______ 种.(用数字作答)
您最近一年使用:0次
7日内更新
|
163次组卷
|
2卷引用:河南省商丘市部分学校2023-2024学年高二下学期期末考试数学试卷
解题方法
3 . 有4名医学毕业生到甲、乙、丙三所学校去应聘校医工作,若每人至多被一所学校录用,每所学校至少录用其中1人,则所有不同的录用情况种数为( ) .
| A.40种 | B.60种 | C.80种 | D.120种 |
您最近一年使用:0次
解题方法
4 . 现有6位同学报名参加学校的足球、篮球等5个不同的社团活动,每位同学只能参加一个社团,且每个社团都要有同学参加,在小华报名参加足球社团的条件下,有两名同学参加足球社团的概率为__________ .
您最近一年使用:0次
5 .  ,
, ,
, 三所大学发布了面向高二学生的夏令营招生计划,每位学生只能报一所大学.某中学现有四位学生报名.若每所大学都有该中学的学生报名,则不同的报名方法共有( )
三所大学发布了面向高二学生的夏令营招生计划,每位学生只能报一所大学.某中学现有四位学生报名.若每所大学都有该中学的学生报名,则不同的报名方法共有( )
 ,
, ,
, 三所大学发布了面向高二学生的夏令营招生计划,每位学生只能报一所大学.某中学现有四位学生报名.若每所大学都有该中学的学生报名,则不同的报名方法共有( )
三所大学发布了面向高二学生的夏令营招生计划,每位学生只能报一所大学.某中学现有四位学生报名.若每所大学都有该中学的学生报名,则不同的报名方法共有( )| A.30种 | B.36种 | C.72种 | D.81种 |
您最近一年使用:0次
解题方法
6 . 某市人民政府新招聘进 5 名应届大学毕业生,分配给教育、卫生、医疗、文旅四个部门, 每人只去一个部门,若教育部门必须安排 2 人,其余部门各安排 1 人,则不同的方案数为( )
| A.52 | B.60 | C.72 | D.360 |
您最近一年使用:0次
2024-07-20更新
|
917次组卷
|
4卷引用:四川省成都市蓉城名校2023-2024学年高二下学期6月期末联考数学试题
四川省成都市蓉城名校2023-2024学年高二下学期6月期末联考数学试题(已下线)【高二模块一】难度7 小题强化限时晋级练(较难1)新疆阿勒泰地区2023-2024学年高二下学期期末联考数学试卷(已下线)第一章 排列组合与二项式定理 专题三 组合 微点2 组合综合训练【培优版】
7 . 为了支援山区教育,现在安排5名大学生到3个学校进行支教活动,每个学校至少安排1人,其中甲校要安排2名大学生,则不同的安排方法种数为( )
| A.30 | B.60 | C.90 | D.120 |
您最近一年使用:0次
2024-07-20更新
|
183次组卷
|
2卷引用:浙江省环大罗山联盟2023-2024学年高二下学期4月期中考试数学试题
8 . 7名研究人员在3个不同的无菌研究舱同时进行工作,每名研究人员必须去一个舱,且每个舱至少去1人,由于空间限制,每个舱至多容纳3人,则不同的安排方案共有 ( )种.
| A.720 | B.1050 | C.1440 | D.360 |
您最近一年使用:0次
9 . 五一小长假期间,某旅游公司为助力大同旅游事业的发展,计划将2名金牌导游和5名银牌导游分别派往云冈石窟、古城华严寺、北岳恒山三个景区承担义务讲解任务,要求每个景区都要有银牌导游前往,则不同的分配方法种数有( )
| A.360 | B.640 | C.1350 | D.1440 |
您最近一年使用:0次
10 . 北京2022年冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”一亮相,好评不断,这是一次中国文化与奥林匹克精神的完美结合.为了宣传2022年北京冬奥会和冬残奥会,某学校决定派小明和小李等5名志愿者将两个吉祥物安装在学校的体育广场,每人参与且只参与一个吉祥物的安装,每个吉祥物都至少由两名志愿者安装.若小明和小李必须安装不同的吉祥物,则不同的分配方案种数为( )
| A.8 | B.10 | C.12 | D.14 |
您最近一年使用:0次
2024-07-16更新
|
101次组卷
|
2卷引用:北京市中央工艺美术学院附属中学(北京市国际美术学校)2023-2024学年高二下学期期中考试数学试卷



