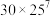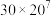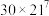解题方法
1 . 每年5月17日为国际电信日,某市电信公司每年在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.根据以往的统计结果绘出电信日当天参与活动的统计图,现将频率视为概率.

(1)求某两人选择同一套餐的概率;
(2)若用随机变量 表示某两人所获优惠金额的总和,求
表示某两人所获优惠金额的总和,求 的分布列和数学期望.
的分布列和数学期望.

(1)求某两人选择同一套餐的概率;
(2)若用随机变量
 表示某两人所获优惠金额的总和,求
表示某两人所获优惠金额的总和,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2011·山西忻州·一模
名校
2 . 在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足sin A+ cos A=2.
cos A=2.
(1)求角A的大小;
(2)现给出三个条件:①a=2;②B=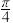 ;③c=
;③c= b.试从中选出两个可以确定△ABC的条件,写出你的方案并以此为依据求△ABC的面积.(写出一种方案即可)
b.试从中选出两个可以确定△ABC的条件,写出你的方案并以此为依据求△ABC的面积.(写出一种方案即可)
 cos A=2.
cos A=2.(1)求角A的大小;
(2)现给出三个条件:①a=2;②B=
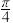 ;③c=
;③c= b.试从中选出两个可以确定△ABC的条件,写出你的方案并以此为依据求△ABC的面积.(写出一种方案即可)
b.试从中选出两个可以确定△ABC的条件,写出你的方案并以此为依据求△ABC的面积.(写出一种方案即可)
您最近一年使用:0次
2020-09-13更新
|
1193次组卷
|
20卷引用:2011年全国高中数学联赛黑龙江赛区预赛试题
(已下线)2011年全国高中数学联赛黑龙江赛区预赛试题(已下线)2011届山西省忻州市高三第一次联考数学文卷(已下线)2010-2011年江苏省如皋市五校高二下学期期中考试文科数学(已下线)2013届河北省唐山市第一中学高三第一次月考文科数学试卷2015-2016学年浙江省金华等三市部分学校高一下3月联考数学试卷2015-2016学年黑龙江大庆市铁人中学高一下期中文数学卷2017届新疆生产建设兵团二中高三上月考二数学(理)试卷河南省信阳市普通高中2018届高三第一次教学质量检测数学(文)试题西藏拉萨市2019-2020学年高二上学期期末联考数学(理)试题辽宁省辽宁师范大学附属中学2019-2020学年高一下学期期末数学试题西藏拉萨市第二高级中学2019-2020学年高二上学期期中考试数学试题河南省周口市中英文学校2020-2021学年高二上学期第一次月考数学试题西藏拉萨第二高级中学2020-2021学年高二(上)期中数学试题广东省梅州市大埔县虎山中学2020-2021学年高一下学期期中数学试题辽宁省六校协作体2020-2021学年高一下学期期中数学试题广东省韶关市第五中学2021-2022学年高二上学期期中数学试题山东省临沂第四中学2021-2022学年高一下学期3月阶段性达标检测数学试题河南省周口市扶沟县第二高级中学2021-2022学年高二上学期第一次摸底考试数学试题河南省周口市扶沟县第二高级中学2021-2022学年高二第一次摸底数学试题宁夏吴忠市吴忠中学2022-2023学年高二上学期期中考试数学(理)试题
名校
3 . 某省 年开始将全面实施新高考方案.在
年开始将全面实施新高考方案.在 门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为
门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为 ,
, ,
, ,
, ,
, 共
共 个等级,各等级人数所占比例分别为
个等级,各等级人数所占比例分别为 、
、 、
、 、
、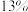 和
和 ,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
(1)某校生物学科获得 等级的共有10名学生,其原始分及转换分如下表:
等级的共有10名学生,其原始分及转换分如下表:
现从这10名学生中随机抽取3人,设这3人中生物转换分不低于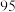 分的人数为
分的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)假设该省此次高一学生生物学科原始分 服从正态分布
服从正态分布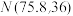 .若
.若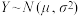 ,令
,令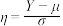 ,则
,则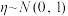 ,请解决下列问题:
,请解决下列问题:
①若以此次高一学生生物学科原始分 等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
②现随机抽取了该省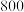 名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记
名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记 为被抽到的原始分不低于
为被抽到的原始分不低于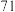 分的学生人数,求
分的学生人数,求 取得最大值时
取得最大值时 的值.
的值.
附:若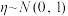 ,则
,则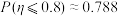 ,
, .
.
 年开始将全面实施新高考方案.在
年开始将全面实施新高考方案.在 门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为
门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为 ,
, ,
, ,
, ,
, 共
共 个等级,各等级人数所占比例分别为
个等级,各等级人数所占比例分别为 、
、 、
、 、
、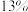 和
和 ,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.(1)某校生物学科获得
 等级的共有10名学生,其原始分及转换分如下表:
等级的共有10名学生,其原始分及转换分如下表:| 原始分 | 91 | 90 | 89 | 88 | 87 | 85 | 83 | 82 |
| 转换分 | 100 | 99 | 97 | 95 | 94 | 91 | 88 | 86 |
| 人数 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 1 |
现从这10名学生中随机抽取3人,设这3人中生物转换分不低于
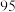 分的人数为
分的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)假设该省此次高一学生生物学科原始分
 服从正态分布
服从正态分布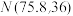 .若
.若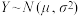 ,令
,令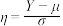 ,则
,则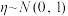 ,请解决下列问题:
,请解决下列问题:①若以此次高一学生生物学科原始分
 等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)②现随机抽取了该省
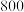 名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记
名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记 为被抽到的原始分不低于
为被抽到的原始分不低于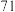 分的学生人数,求
分的学生人数,求 取得最大值时
取得最大值时 的值.
的值.附:若
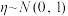 ,则
,则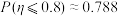 ,
, .
.
您最近一年使用:0次
2020-06-05更新
|
4450次组卷
|
17卷引用:福州市2020届高三毕业班第三次质量检查理科数学试题
福州市2020届高三毕业班第三次质量检查理科数学试题江苏省苏州市2020-2021学年高三上学期9月期初调研数学试题山东省泰安市2019-2020学年下学期高二期末考试数学试题江苏省扬州市高邮市第一中学2020-2021学年高三上学期9月阶段性测试数学试题江苏省苏州市相城区陆慕高级中学2020-2021学年高三上学期期初数学试题2023年全国中学生数学能力测评(终评)高三年级组试题江苏省南京市第十三中学2021-2022学年高二下学期初数学试题(已下线)专题12 四大分布:两点分布、超几何分布、二项分布、正态分布-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)专题14 概率、统计、期望(已下线)专题9-1 概率与统计及分布列归类(理)(讲+练)-1(已下线)第四篇 概率与统计 专题2 最可能成功次数 微点1 最可能成功次数广东省茂名市华南师范大学附属电白学校2023届高三下学期5月调研数学试题(已下线)第四篇 概率与统计 专题7 常见分布 微点2 其它分布(已下线)结业测试卷(范围:第五、六、七章)(提高篇)-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)河南省南阳市2023-2024学年高二上学期期终质量评估数学试题(已下线)第1讲:二项式定理和二项分布的最值问题【练】(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点2 重要的概率分布模型(二)【基础版】
4 . 有2002名运动员,号码依次为 .从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,被选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
.从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,被选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
 .从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,被选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
.从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,被选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
您最近一年使用:0次
2002高三·湖南·竞赛
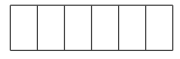
5 . 在如图 所示的 6 块地上, 种上甲或乙两种蔬菜(可只种其中一种, 也可两种都种).要求相邻 2 块土地上不都种甲种蔬菜, 则共有种蔬菜的方案数为__________ .

您最近一年使用:0次
6 . 现安排7名同学去参加5个运动项目,要求甲、乙两同学不能参加同一个项目,每个项目都有人参加,每人只参加一个项目.则满足上述要求的不同安排方案数为______ (用数字作答).
您最近一年使用:0次
2018-12-25更新
|
261次组卷
|
3卷引用:数学奥林匹克高中训练题(214)
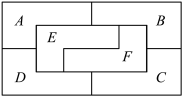
7 . 用红、黄、蓝、白四种颜色对图所示的区域染色,要求任何两个相邻区域(有公共边界)的颜色均不相同.则一共有______ 种染色方案.

您最近一年使用:0次
8 . 某科室安排甲、乙、丙、丁四人国庆节放假期间(共放假八天)的值班表.已知甲、乙各值班四天,甲不能在第一天值班且甲、乙不在同一天值班;丙需要值班三天,且不能连续值班;丁需要值班五天;规定每天必须两人值班.则符合条件的不同方案共有( )种.
| A.400 | B.700 | C.840 | D.960 |
您最近一年使用:0次
9 . 将正整数1,2,…,10填于正五角星的十个顶点处,使得每条直线上所填四个数之和相等,问:这种填数方案是否存在?若存在,请给出填数方案的个数(经过旋转或对称之后能重合的方案视为同一种方案);若不存在,请说明理由.
您最近一年使用:0次

 ,长
,长 .用6种颜色的
.用6种颜色的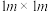 的整块地砖来铺设(每块地砖都是单色的,每种颜色的地砖都足够多),要求相邻的两块地砖颜色不同.那么,所有的不同拼色方案种数为(
的整块地砖来铺设(每块地砖都是单色的,每种颜色的地砖都足够多),要求相邻的两块地砖颜色不同.那么,所有的不同拼色方案种数为(